1.最大矩形

难度困难

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。
示例:
输入:
[
[“1”,”0”,”1”,”0”,”0”],
[“1”,”0”,”1“,”1“,”1“],
[“1”,”1”,”1“,”1“,”1“],
[“1”,”0”,”0”,”1”,”0”]
]
输出: 6

2.基本题——数组的最大面积

给定数组arr，其中arr[i]表示1为底，高为arr[i]的矩形，则数组arr可以表示一个柱状图。这里求该柱状图所包含的矩形中，面积最大的矩形。
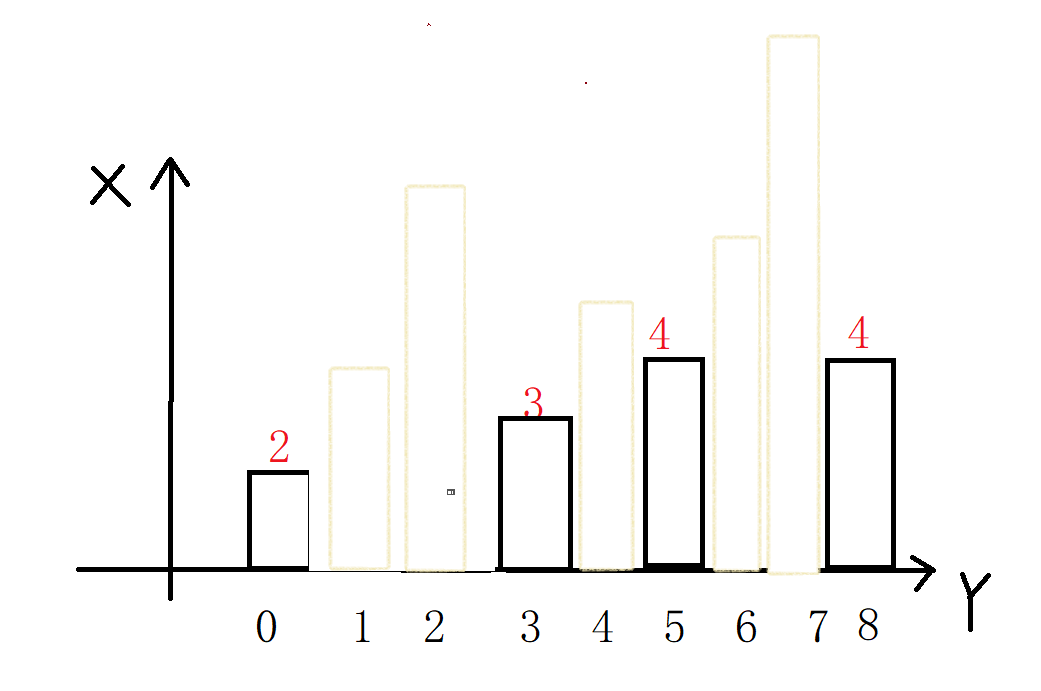
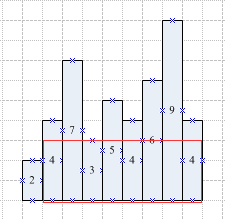
例如：int arr[] = {2, 4, 7, 3, 5, 4, 6, 9, 4};
则该数组可表示如下的柱状图：

在该柱状图中，面积最大矩形是8 * 3 = 24；

思路：这道题用单调栈解决会很方便

单调栈：栈的一种，其内元素按照从小到大（或者从大到小）递增（递减）的栈

针对数组{2, 4, 7, 3, 5, 4, 6, 9, 4}

1. 首先构造一个单调递增栈。

   为什么选取单调递增栈呢？因为此题需要求最大面积，如果选用单调递减栈，当一个元素出栈的时候，其两边并不是该矩形所能扩的最远位置！当选用递增栈的时候，因为两边高度都比他小，所以该矩形能扩的区域是确定的。

2. 不断入栈，碰到比栈顶元素小的元素，循环让其出栈，并计算出栈元素所能形成的最大矩形区域。如下图所示，2，4，7 按照递增顺序入栈（下标），此时由于 3 比栈顶元素 7 小，所以栈顶需要弹出
   
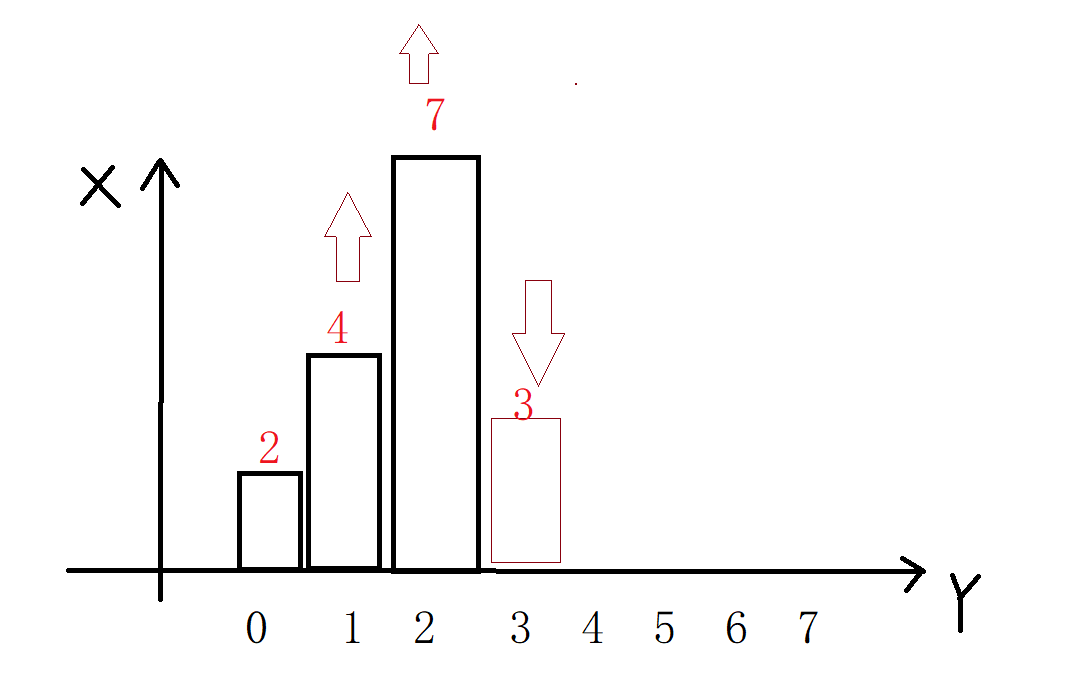
   此时 7 的右边界已经找到，即当前的 下标3。而 7 的左边界就是其栈的下一个元素 4 的下标1，由此可以计算出 7 所能扩出的最大矩形面积 即 7 * (3 - 1 - 1) = 7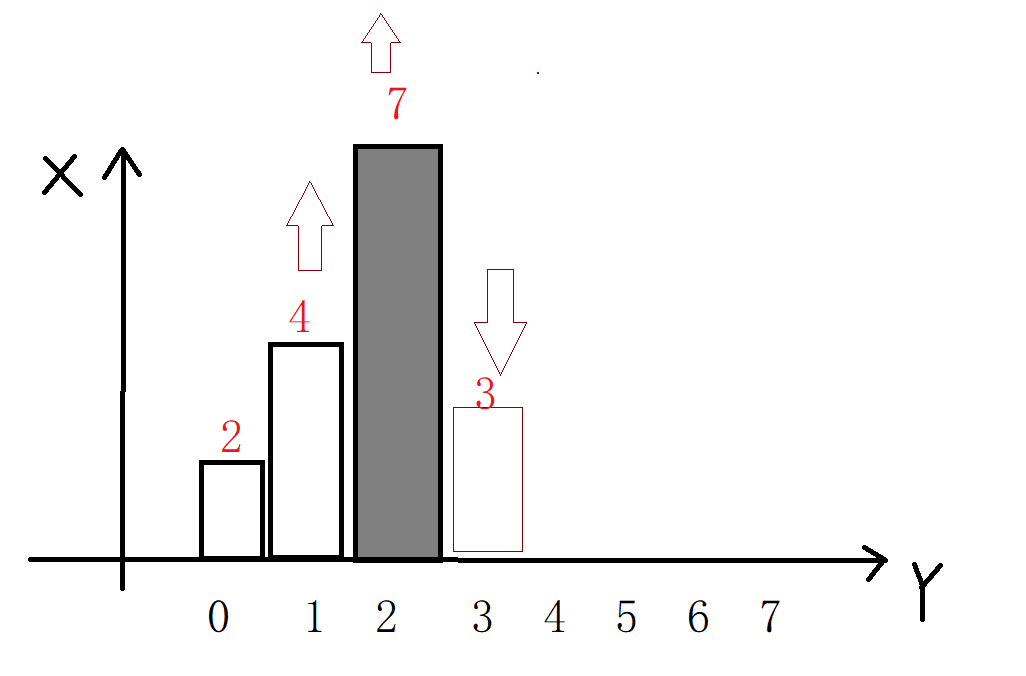
   

3. 元素 7 弹出之后，由于 4 也比 3 大，所以 4 也需要弹出，过程同上，如下图，4 此时的面积为：
   4 * (3 - 0 - 1)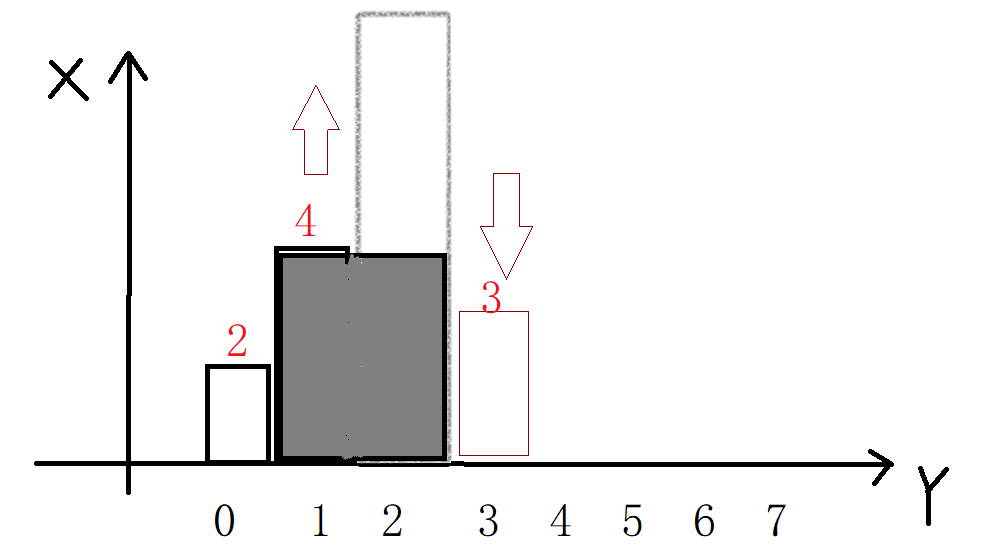
   

4. 当遍历完成之后，栈内所剩元素如下，我们可以发现每个元素都能向右扩到数组的最右端，左边界就是栈内下一个元素的位置！！！
   

话不多说，上代码：

public int getMaxArea(int[] nums) {
        Stack<Integer> stack = new Stack<>(); //设置一个从小到大单调栈
        int left = 0;
        int max = 0;
        for (int i = 0; i < nums.length; i++) {
            while (!stack.isEmpty() && nums[i] < nums[stack.peek()]) {
                int cur = stack.pop();
                left = stack.isEmpty() ? 0 : stack.peek() + 1; 
                //左边界为 stack.peek() + 1，但要注意空栈的处理
                max = Math.max(max, nums[cur] * (i - left));
                //右边界为当前 i ！
            }
            stack.push(i);
        }
        while (!stack.isEmpty()) {
            int cur = stack.pop();
            left = stack.isEmpty() ? 0 : stack.peek() + 1;
            max = Math.max(max, nums[cur] * (nums.length - left));
            //右边界此时为数组的最右端
        }
        System.out.println(max);
        return max;
    }

回到第一题

仔细一想，其实求二维数组中包含1的最大矩形的面积与上面的过程大同小异：在遍历每一层的时候，将上面的1累加，作为当前的高度，但要注意一旦该层有0，则是无法形成具有高度的柱子的！
代码如下：

public int maximalRectangle(char[][] matrix) {
        if(matrix==null||matrix.length==0){
            return 0;
        }
        int[] ddx = new int[matrix[0].length];
        int max =0;
        for(int i=0;i<matrix.length;i++){
            for(int j=0;j<matrix[i].length;j++){
                ddx[j]=(matrix[i][j] == '0' )? 0:ddx[j]+1;
            }

            max=Math.max(max,getMaxArea(ddx));
        }
        return max;
    }

延申题——看到楼的数量

小Q在周末的时候和他的小伙伴来到大城市逛街，一条步行街上有很多高楼，共有n座高楼排成一行。
小Q从第一栋一直走到了最后一栋，小Q从来没有看到过这么多高楼，所以他想知道他在每栋楼的位置处能看到多少栋楼呢？（当前面的楼的高度大于等于后面的楼时，后面的楼将被挡住）
输入描述：
输入第一行将包含一个数字n,表示楼的栋数，接下来的一行将包含n个数字wi(1<=i<=n)，代表一栋楼的高度。
1<=n<=100000;
1<=wi<=100000;
输出描述：
输出一行，包含空格分隔的m个数字vi,分别代表小Q在第i栋楼的时候能看到的楼的数量。

思路

此题用单调栈就非常清晰，先正向遍历一遍，看每个楼左边能看到楼的数量，再反向遍历一遍，求出每个楼右边看到的楼的数量，最后相加即可！

public static void getSeeCounts(int[] height) {
        Stack<Integer> stack = new Stack<>(); //维护一个从大到小单调栈,因为当前位置的楼只能看到左边或右边递增的楼，看不到递减的楼
        int len = height.length;
        int[] left_Count = new int[len]; //记录每个楼左边看到楼的数量
        int[] right_Count = new int[len];//记录每个楼右边看到楼的数量
        for (int i = 0; i < height.length; i++) {
            left_Count[i] = stack.size();
            while(!stack.isEmpty() && height[i] > height[stack.peek()]){
                stack.pop();
            }
            stack.push(i);
        }
        stack.clear();
        for (int i = len - 1; i >= 0; i--) {
            right_Count[i] = stack.size(); 
            //每个楼能看到的就是当前递增楼的数量，即单调栈的容量
            while(!stack.isEmpty() && height[i] > height[stack.peek()]){
                stack.pop();
            }
            stack.push(i);
        }
        for(int i = 0;i<len;i++){
            left_Count[i]+=right_Count[i] + 1; //加一是因为还有自己本身
        }

        System.out.println(Arrays.toString(left_Count));
        System.out.println(Arrays.toString(right_Count));
    }

本作品采用《CC 协议》，转载必须注明作者和本文链接