01 矩阵

难度中等

给定一个由 0 和 1 组成的矩阵，找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。

示例 1:
输入:
0 0 0
0 1 0
1 1 1
输出:
0 0 0
0 1 0
1 2 1

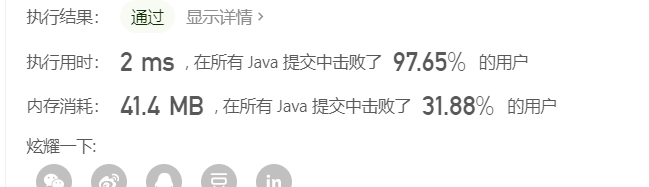
1. 解决这个问题先来一个问题 : 岛屿数量

岛屿数量这个问题是在给定一个二维数组，找出 1 连成一片的区域的数量
输入:
[
[‘1’,’1’,’0’,’0’,’0’],
[‘1’,’1’,’0’,’0’,’0’],
[‘0’,’0’,’1’,’0’,’0’],
[‘0’,’0’,’0’,’1’,’1’]
]
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。

岛屿数量解题思路可以是通过 DFS ，即深度优先遍历，通过将走过的 1 置成 一个特殊状态，表明该区域已经属于一个岛屿了，直到再上下左右上无法继续延申即可

class Solution {
    public int numIslands(char[][] grid) {
        if(grid==null||grid.length==0){
            return 0;
        }
        int row = grid.length;
        int col = grid[0].length;
        int count=0;
        //岛屿数量
        for(int i=0;i<row;i++){
            for(int j=0;j<col;j++){
                if(grid[i][j]=='1'){
                    count++;
                    infect(grid,i,j);
                }
            }
        }
        return count;
    }
    //感染函数
    public void infect(char[][] ddx ,int i,int j){
        if(i>=ddx.length||j>=ddx[0].length||i<0||j<0||ddx[i][j]!='1'){
            return;
        }
        ddx[i][j]='2'; //将走过的 1 感染成 2 ，代表这个 1已经属于当前陆地了
        infect(ddx,i+1,j);
        infect(ddx,i-1,j);
        infect(ddx,i,j+1);
        infect(ddx,i,j-1);
    }
}

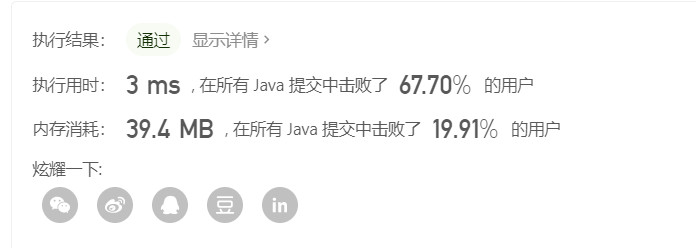
2.再看一个关于岛屿的问题 ： 岛屿的最大面积

岛屿的最大面积和岛屿数量类似，只不过需要求岛屿的最大面积，即 1 连成一片的区域的最大值
示例 1:
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1

解题方法与上面的类似，只不过每次需要更新岛屿面积的最大值！

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        if(grid==null||grid.length==0||grid[0]==null||grid[0].length==0){
            return 0;
        }
        int row = grid.length;
        int col = grid[0].length;
        int max =0;
        for(int i=0;i<row;i++){
            for(int j=0;j<col;j++){
                if(grid[i][j]==1){
                    max = Math.max(max,infect(grid,i,j,row,col));
                }
            }
        }
        return max;
    }
    public int infect(int[][] grid,int i,int j,int row,int col){
        if(i<0||i>=row||j<0||j>=col||grid[i][j]!=1){
            return 0;
        }
        grid[i][j]=2;//代表当前 1 已经被使用！
        int res = 1; //初始化面积为1
        //之后深度优先，四个方向扩散！
        res+=infect(grid,i,j-1,row,col);
        res+=infect(grid,i,j+1,row,col);
        res+=infect(grid,i+1,j,row,col);
        res+=infect(grid,i-1,j,row,col);
        return res;
    }
}

3.最后这个 01 矩阵问题其实也类似，也可以用上面这种 DFS 来做，以每个 1 出发碰到 0 就返回，但是时间复杂度很高，提交的时候是超时的。

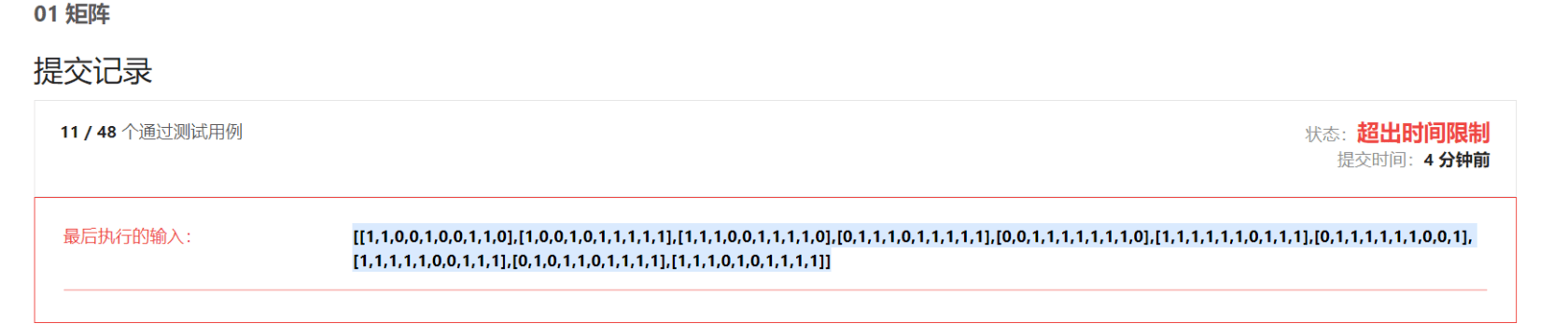
在这提供几种思路：

1.DP

以下为个人理解：因为在遍历数组中的 1 的时候，如果是正向遍历，那么其实有两个方向的信息是已经知道的，即左方向和上方向，这两个方向的信息已经收集好了，可以直接用。同样，反向遍历也一样，下方向和右方向同样是已经收集好，故可以通过正反方向两次遍历，来对指定位置的值进行修正更新！一开始不太容易想，因为很容易陷入一次遍历只能获得上面和左面元素的信息，没有下面和右面元素的信息这种思维，确实，一次遍历并不足以将子问题的信息全部收集到，所以需要第二次遍历来进行修正!

class Solution {

    public int[][] updateMatrix(int[][] matrix) {
        int len = matrix.length;
        int width = matrix[0].length;
        for(int i = 0 ;i < len;i++){
            for(int j = 0; j < width;j++){
                 if(matrix[i][j] == 1){
                        matrix[i][j] = 10000; //先赋一个大值
                    }
                if(i > 0){ //处于第一层的话是没有上面的信息的
                    matrix[i][j] = Math.min( matrix[i][j],matrix[i -1][j] + 1); //上面位置的信息   
                }
                if(j > 0){ //处于第一列的话是没有左面的信息的
                    matrix[i][j] = Math.min(matrix[i][j],matrix[i][j - 1] + 1); //左面位置的信息
                }
            }
        }
        //同上
        for(int i = len - 1;i >= 0;i--){
            for(int j = width - 1; j >= 0; j--){
                if(i < len -1){
                    matrix[i][j] = Math.min( matrix[i][j],matrix[i + 1][j] + 1); //下面位置的信息
                }
                if(j < width - 1){
                    matrix[i][j] = Math.min( matrix[i][j],matrix[i][j + 1] + 1); //右面位置的信息
                }
            }
        }
        return matrix;
    }


}

2.BFS

思路：引自leetcode - 甜姨
对于 「Tree 的 BFS」 （典型的「单源 BFS」） 大家都已经轻车熟路了：
首先把 root 节点入队，再一层一层无脑遍历就行了。
对于 「图 的 BFS」 （「多源 BFS」） 做法其实也是一样滴～，与 「Tree 的 BFS」的区别注意以下两条就 ok 辣～
Tree 只有 1 个 root，而图可以有多个源点，所以首先需要把多个源点都入队；
Tree 是有向的因此不需要标识是否访问过，而对于无向图来说，必须得标志是否访问过哦！并且为了防止某个节点多次入队，需要在其入队之前就将其设置成已访问！

具体过程看BFS+DP

本作品采用《CC 协议》，转载必须注明作者和本文链接