图论(Graph Theory)

一、介绍

图是用来对对象之间的成对关系建模的数学结构，由”节点”或”顶点”(Vertex）以及连接这些顶点的”边”（Edge）组成。

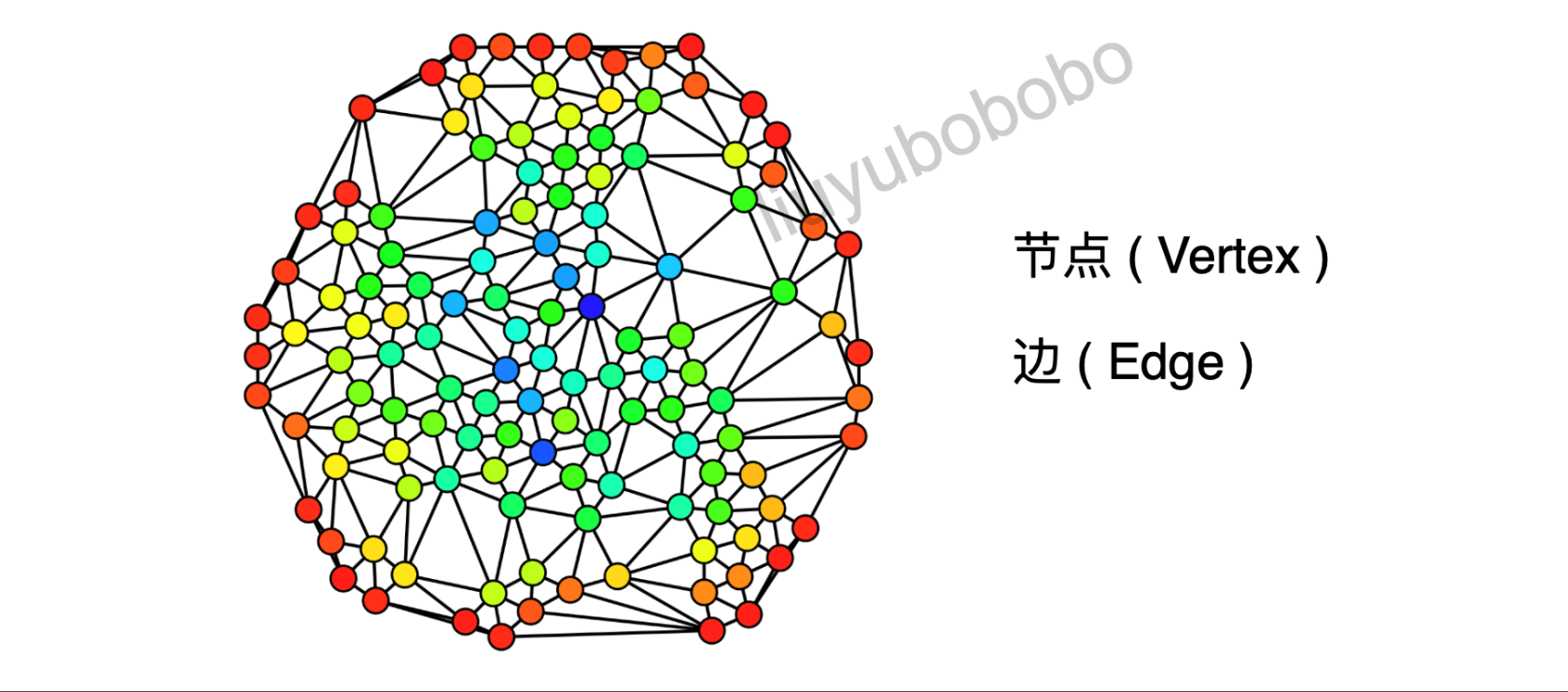
值得注意的是，图的顶点集合不能为空，但边的集合可以为空。图可能是无向的，这意味着图中的边在连接顶点时无需区分方向。否则，称图是有向的。

二、图的分类

1. 图分为：无向图和有向图(无向图是有向图的特殊形式)
   无向图：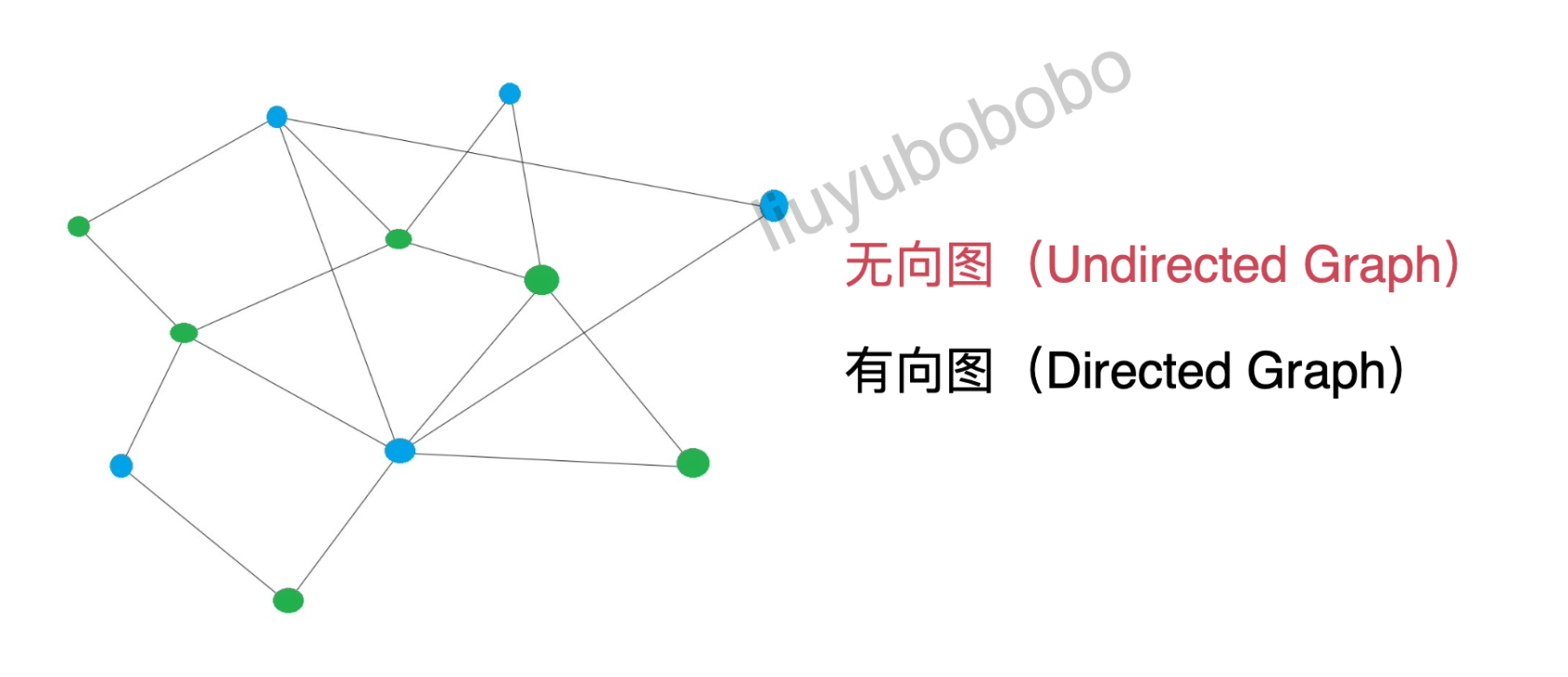
   

有向图：

2. 按权分为：无权图和有权图
   无权图：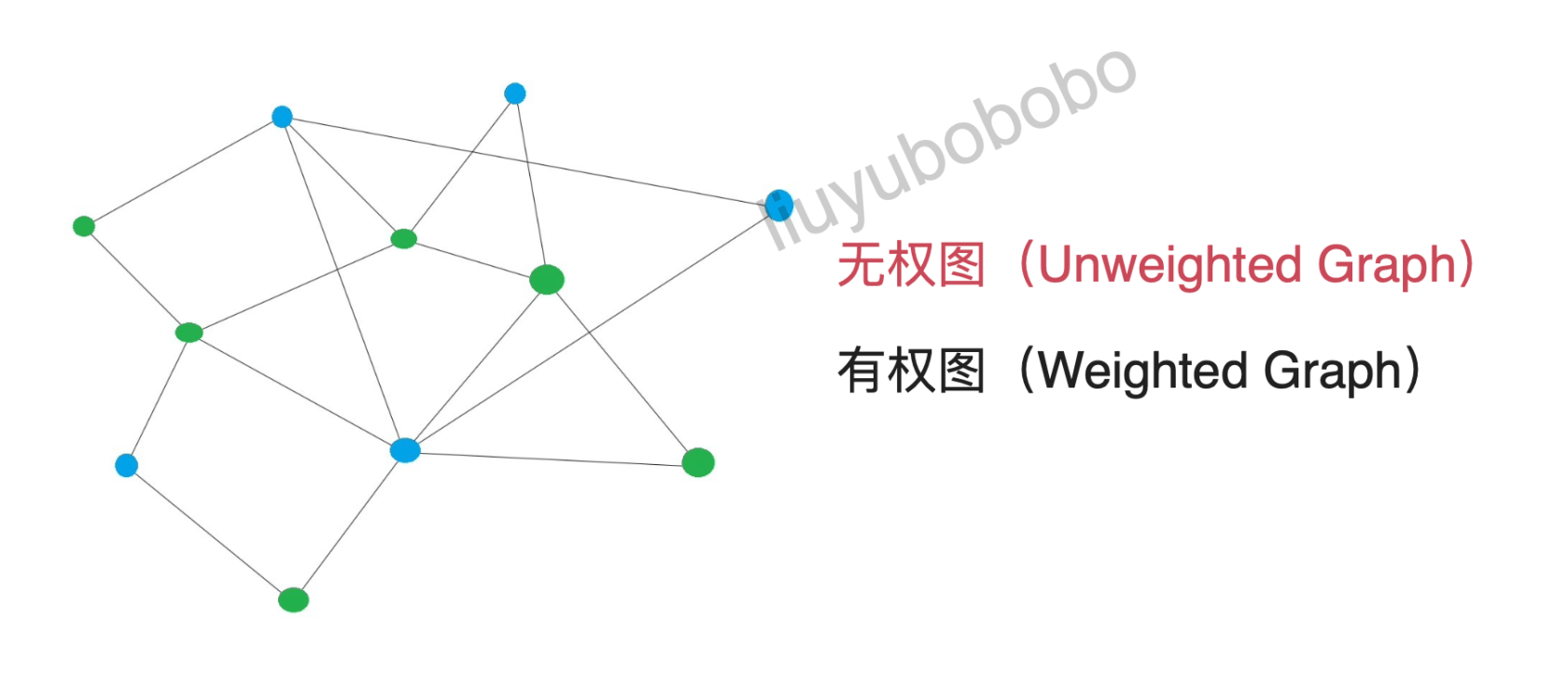
   

有权图：

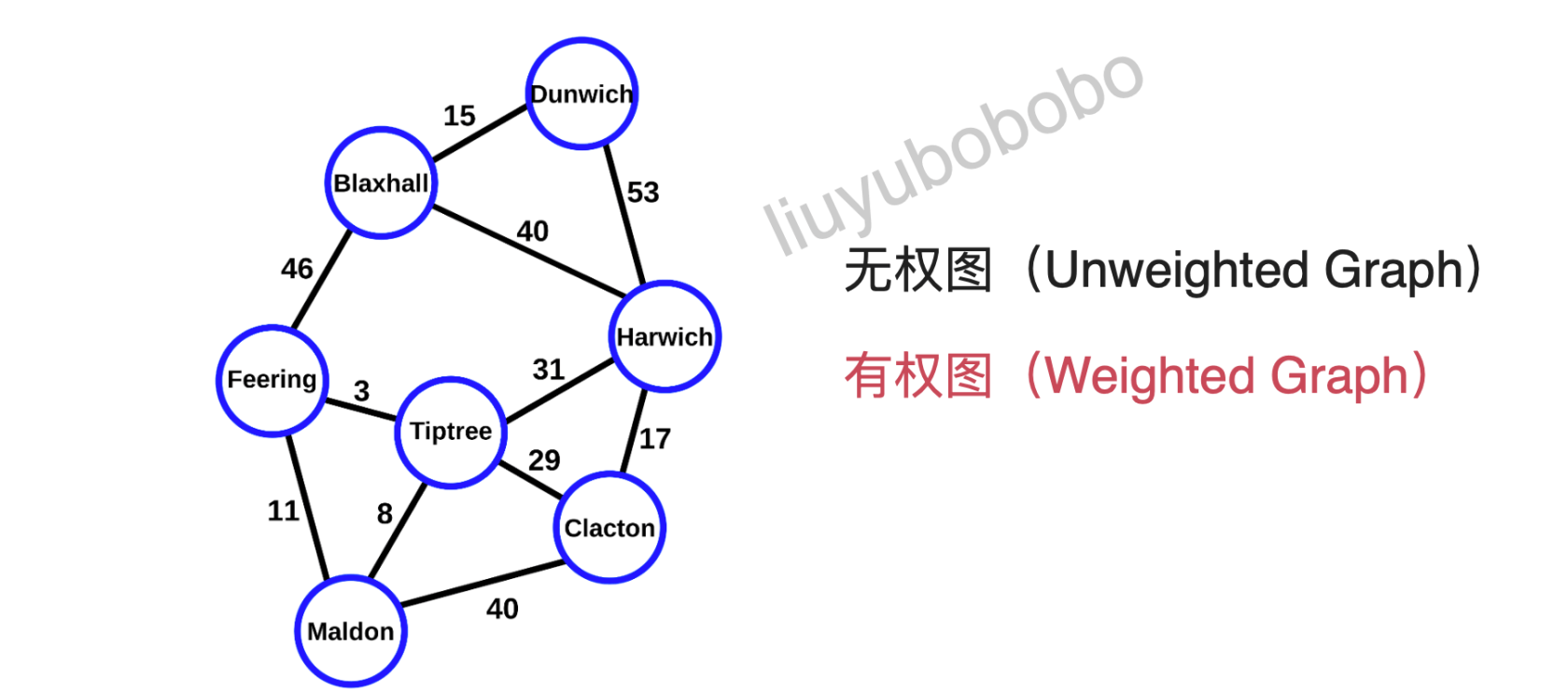
3. 图有平行边，自环边：

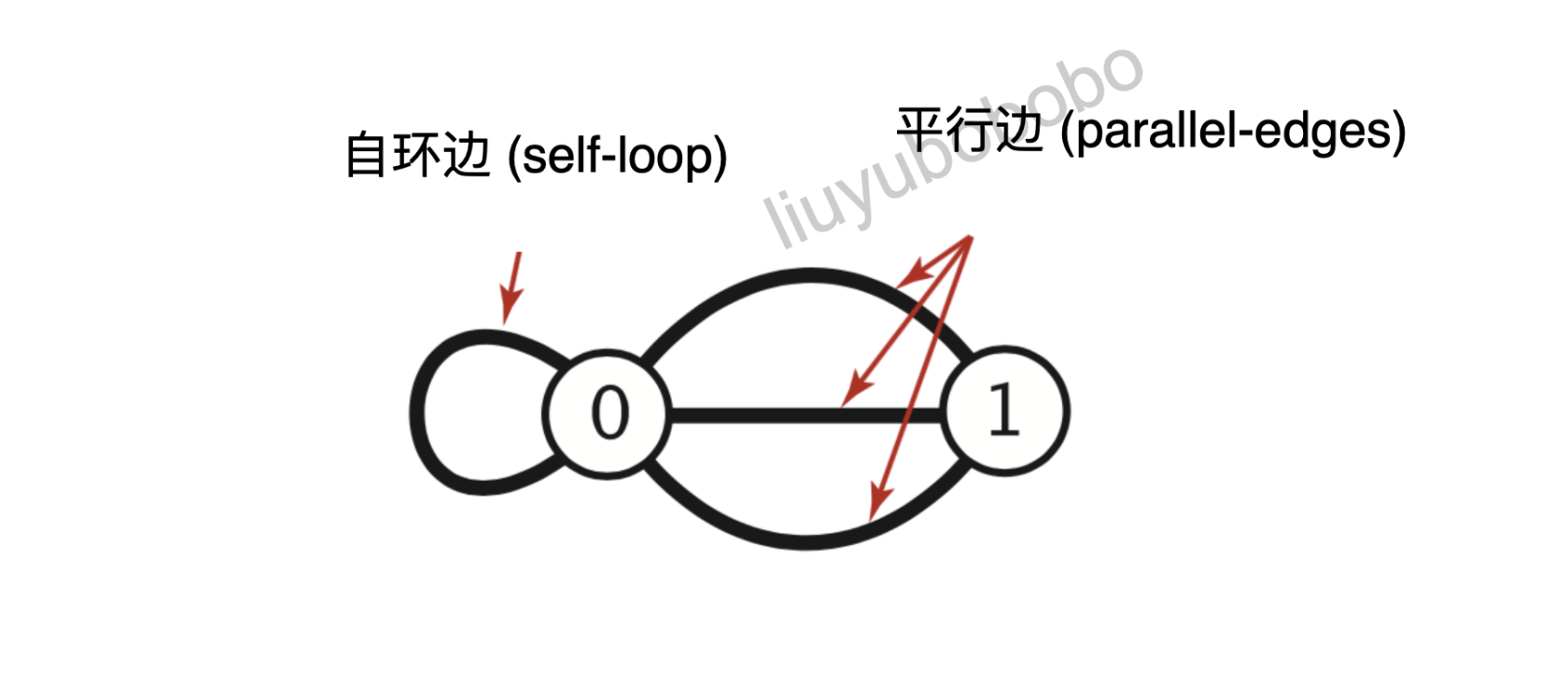
三、图的表示

1. 邻接矩阵：

   0——表示未连接 1——表示连接

• 无向图的邻接矩阵：
  

• 有向图的邻接矩阵：
  

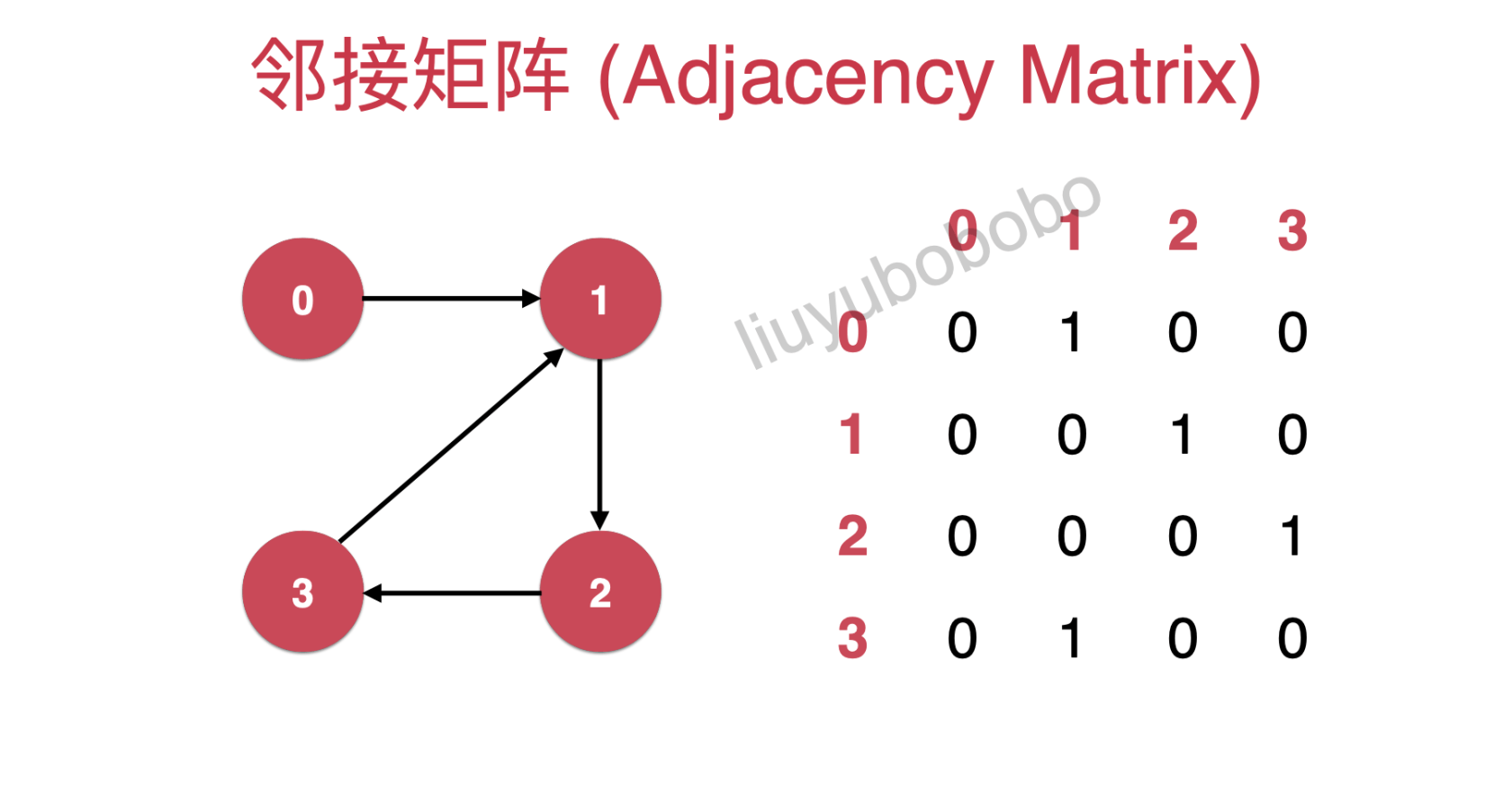
适用说明：邻接矩阵适合表示稠密图

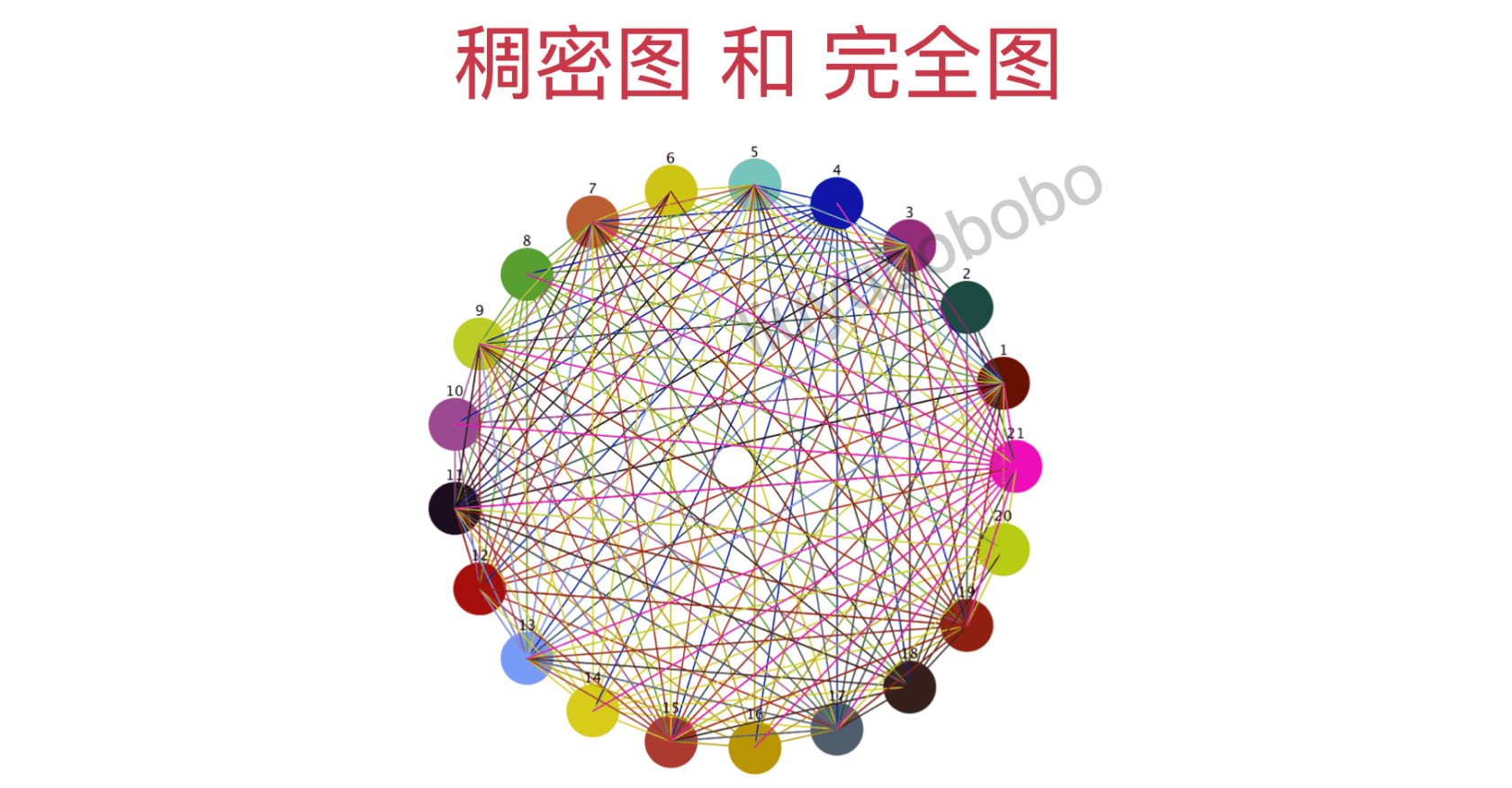
2. 邻接表：

• 无向图的邻接表
  

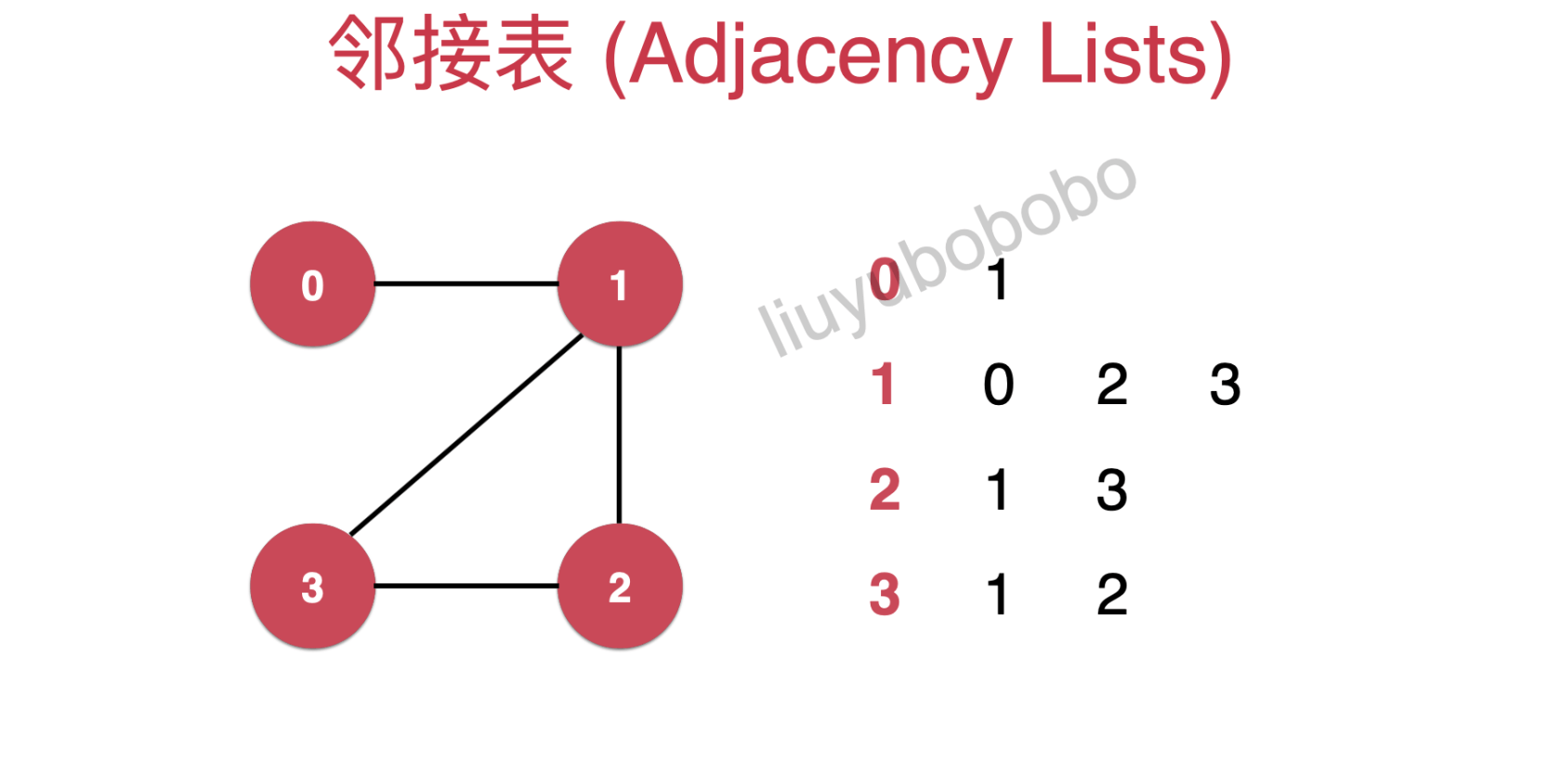
• 有向图的邻接表
  

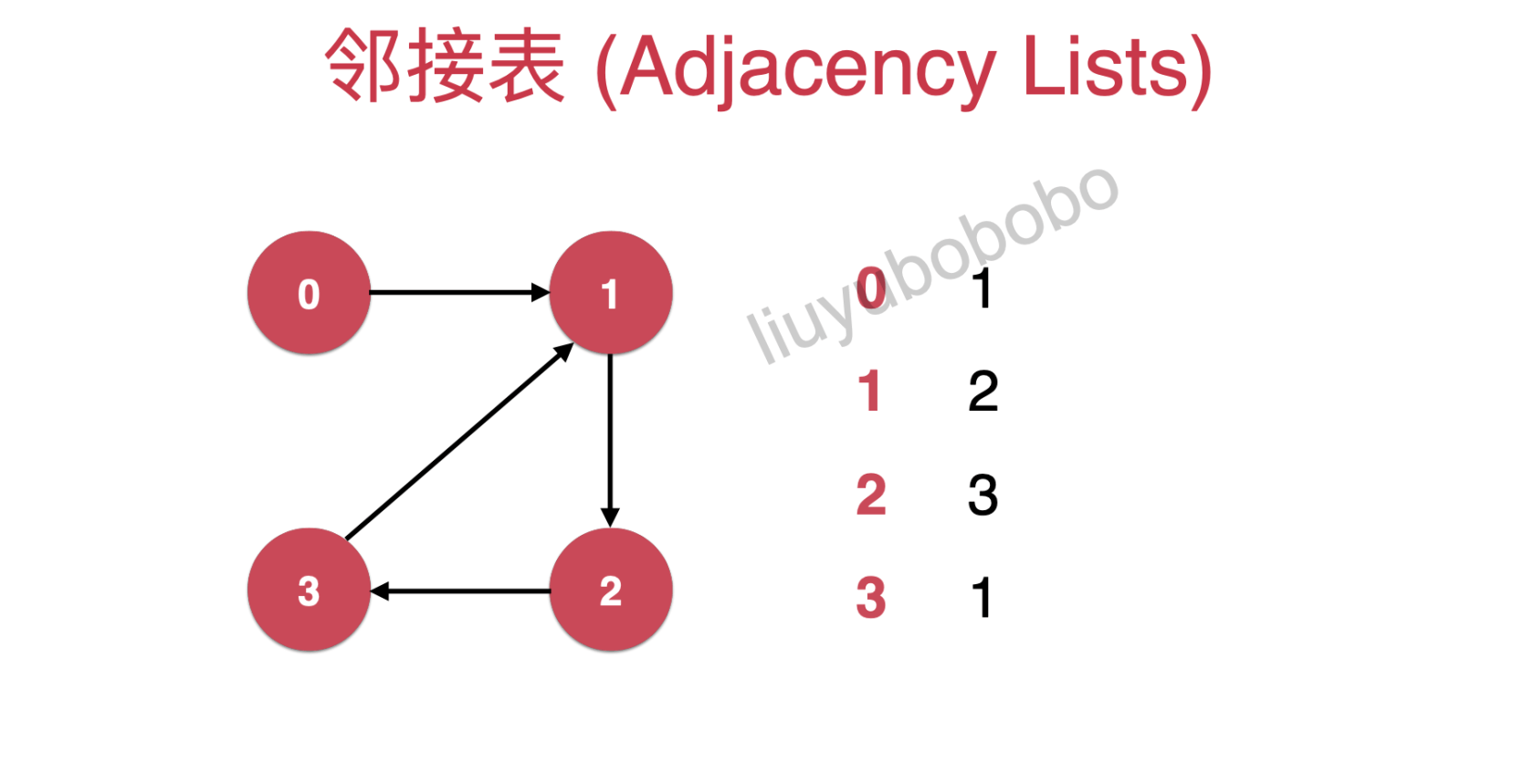
适用说明：邻接表适合表示稀疏图

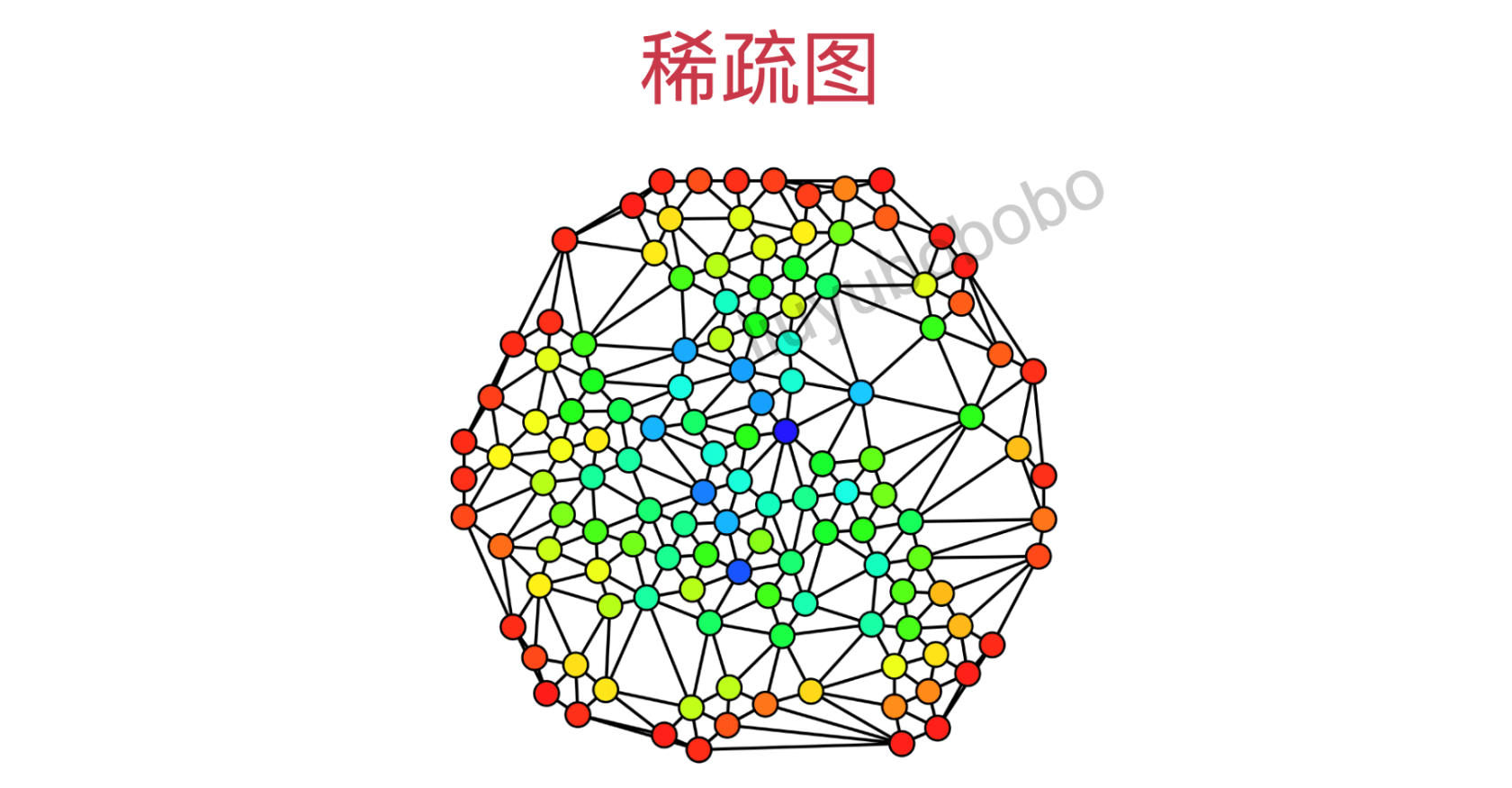
四、稠密图、稀疏图的实现(无权图)

1. 稠密图的实现
   支持的操作有:

• 返回节点数

• 返回边数

• 向图中添加边

• 验证两节点间是否有边

• 显示图的信息

  #include <iostream>
  #include <vector>
  #include <cassert>
  using namespace std;
  //稠密图
  class DenseGraph{
  private:
      int n, m; //节点数和边数
      bool directed; //是否为有向图
      vector<vector<bool>> g; //图的具体数据,0 1 用bool值false和true表示
  public:
      DenseGraph(int n, bool directed){
        assert(n >= 0);
        this->n = n;
        this->m = 0;
        this->directed = directed;
  // g初始化为n*n的布尔矩阵, 每一个g[i][j]均为false, 表示没有任和边
        g = vector<vector<bool>>(n, vector<bool>(n, false));
  }
    //析构函数
    ~DenseGraph(){}
  //返回图中节点的个数
  int getV(){
       return n;
  }
  //返回图中边的条数
  int getE(){
       return m;
  }
  //向图中添加一条边
  void addEdga(int v, int w){
        assert(v >= 0 && v < n);
        assert(w >= 0 && w < n);
        if(hasEdga(v, w)){
             return;
         }
  
        g[v][w] = true;
      //无向图是双向的
        if(!directed){
             g[w][v] = true;
         }
        m++;
  }
  //验证图中是否有v到w的边
  bool hasEdga(int v, int w){
       assert(v >= 0 && v < n);
       assert(w >= 0 && w < n);
       return g[v][w];
  }
  //显示图中信息
  void show(){
      for(int i = 0; i < n; i++){
          for(int j = 0; j < n; j++){
              cout<<g[i][j]<<"\t";
      cout<<endl;
       }
      }
    }
  };

2. 稀疏图的实现

支持的操作有:

• 返回节点数

• 返回边数

• 向图中添加边

• 验证两节点间是否有边

• 显示图的信息

  #include <iostream>
  #include <vector>
  #include <cassert>
  using namespace std;
  //稀疏图—邻接表
  class SparseGraph{
  private:
      int n, m; //节点数和边数
      bool directed; //是否为无向图
      vector<vector<int>> g; //图的具体数据
  public:
     SparseGraph(int n,bool directed){
         assert(n >= 0);
         this->n = n;
         this->directed = directed;
         // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
         g = vector<vector<int>>(n, vector<int>());
  }
    //析构函数
    ~SparseGraph(){}
  
    int getV(){
        return n;
  }
    int getE(){
        return m;
  }
  // 向图中添加一个边
  void addEdga(int v, int w){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
       //将w放入g[v][i]中,将w与v相连
        g[v].push_back(w);
        if(v != w && !directed){
            g[w].push_back(v);
        }
        m ++;
  }
  // 验证图中是否有从v到w的边
  bool hasEdga(int v, int w){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
        for(int i = 0; i <= g[v].size(); i++){
              if(g[v][i] == w)
                   return true;
              return false;  }
  }
  //显示图中信息
  void show(){
      for(int i = 0; i < n; i++){
          cout<<"vector"<<":\t";
          for(int j = 0; j < g[i].size(); j++){
              cout<<g[i][j]<<":\t";
            }
          cout<<endl;
      }
    }
  };
  
  
  

本作品采用《CC 协议》，转载必须注明作者和本文链接