图论系列之「深度优先遍历及联通分量」
图的深度优先遍历及联通分量
一、介绍
深度优先遍历(Depth First Search)的主要思想是首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点。当没有未访问过的顶点时,则回到上一个顶点,继续试探别的顶点,直至所有的顶点都被访问过。
联通分量,无向图 G 的一个极大连通子图称为 G 的一个连通分量(或连通分支)。连通图只有一个连通分量,即其自身;非连通的无向图有多个连通分量。连通分量与连通分量之间没有任何边相连。深度优先遍历可以用来求连通分量。
下图有3个联通分量: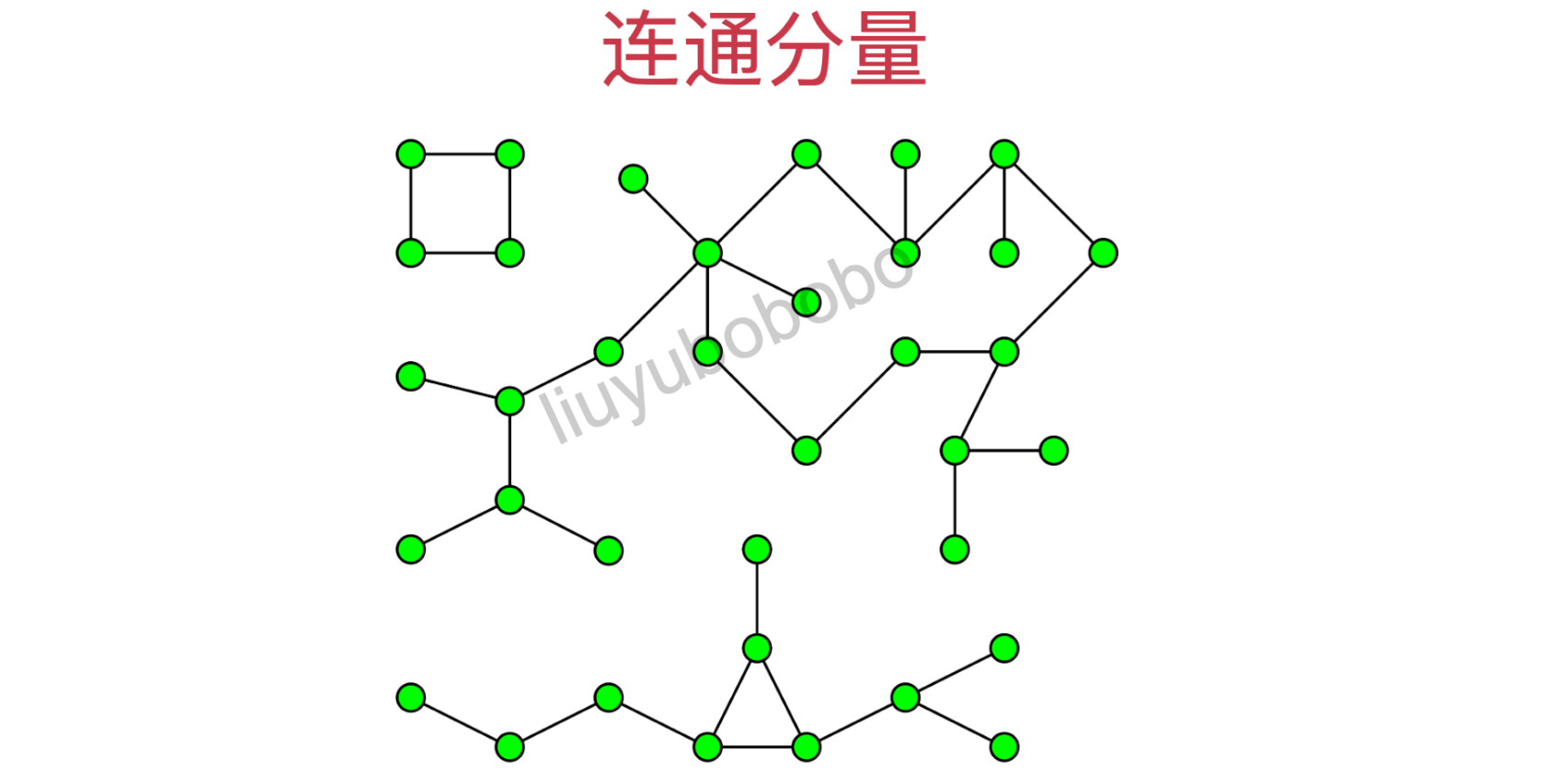
二、遍历过程
如下图:
以邻接表为例
遍历过程中需要注意的是:遍历到x节点时,同样遍历方向会向第x行移动,如果x行为空,则会返回到原来的行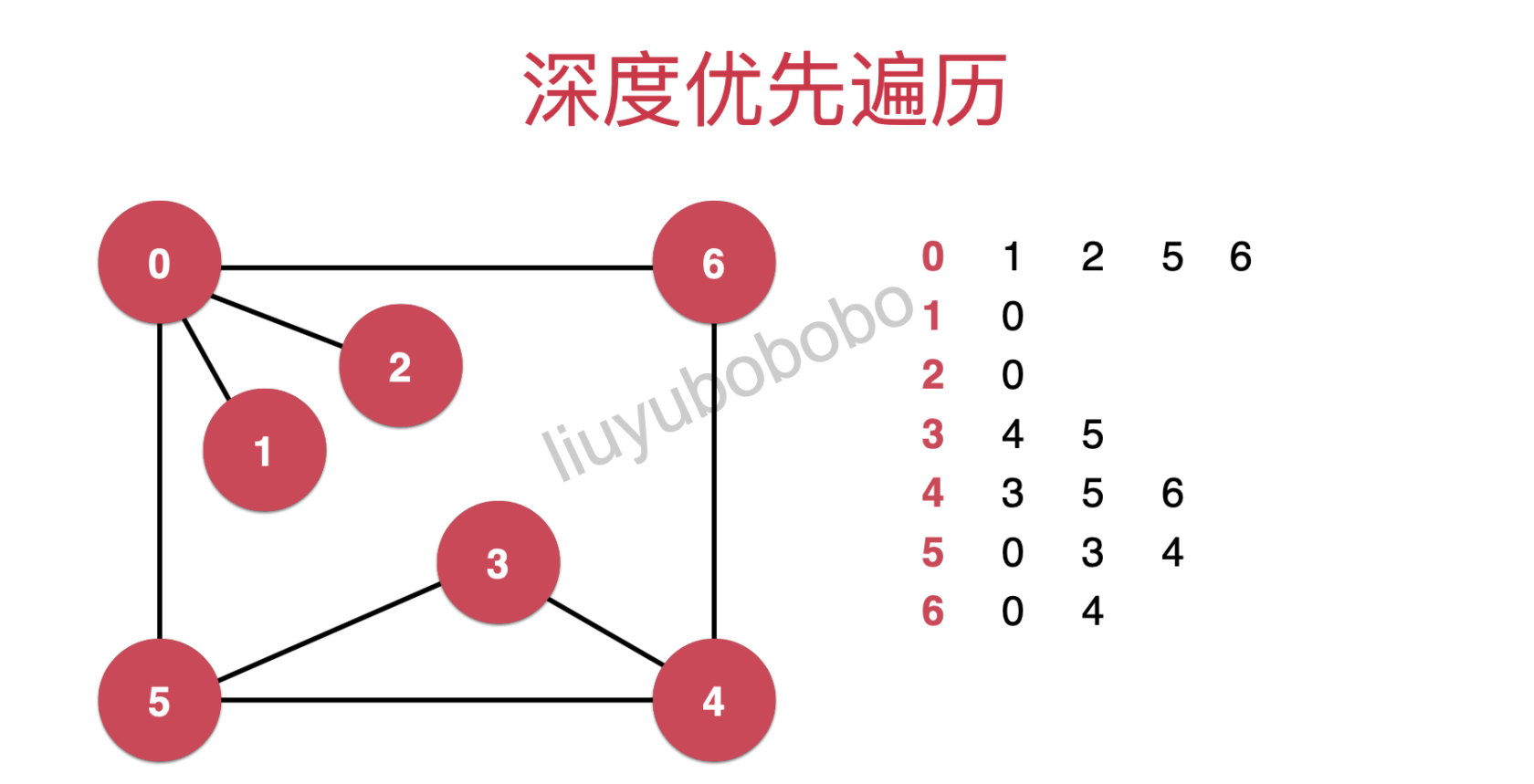
从0开始遍历:(0遍历完后向第0行继续遍历)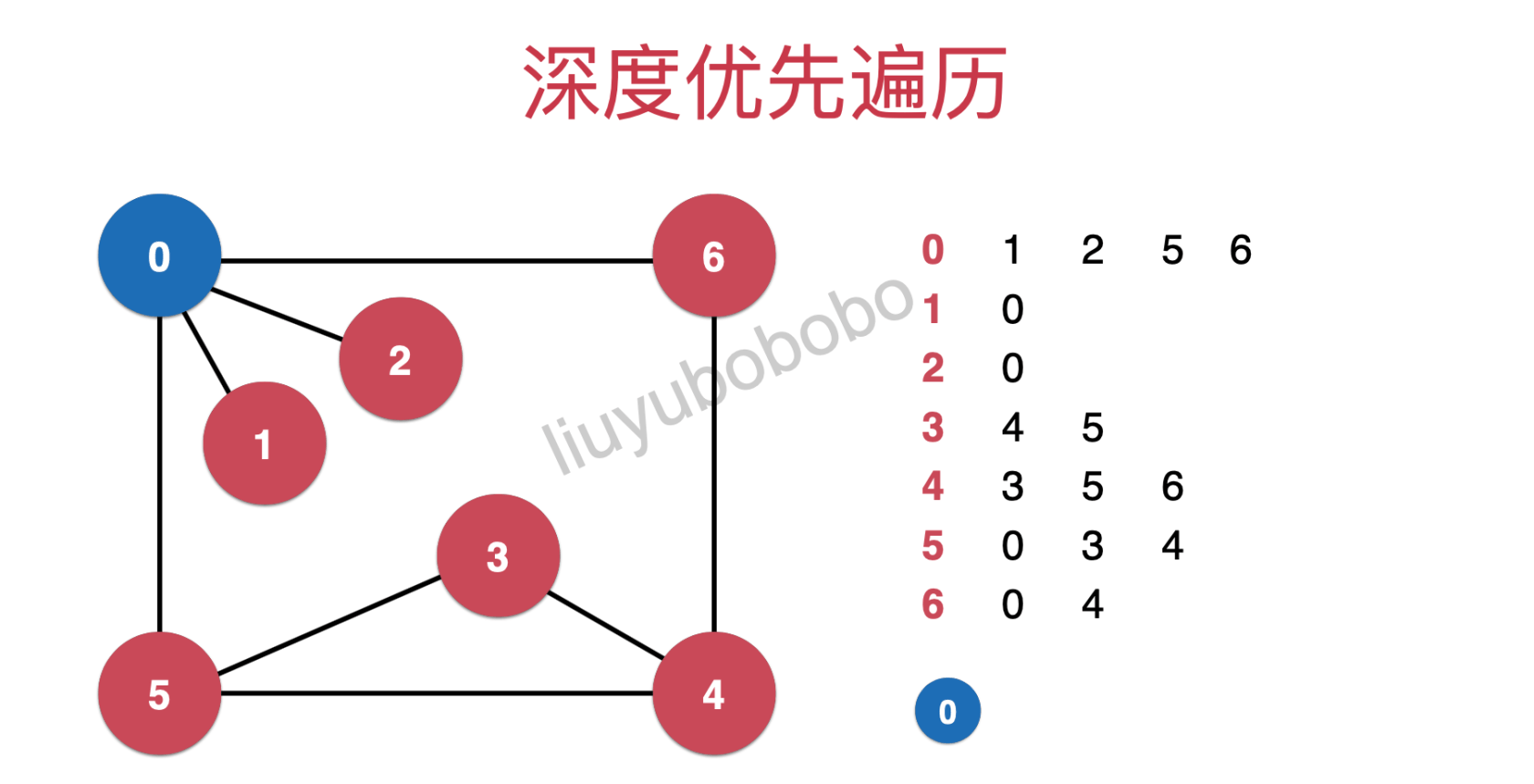
然后遍历1:(遍历1时已经在第1行,)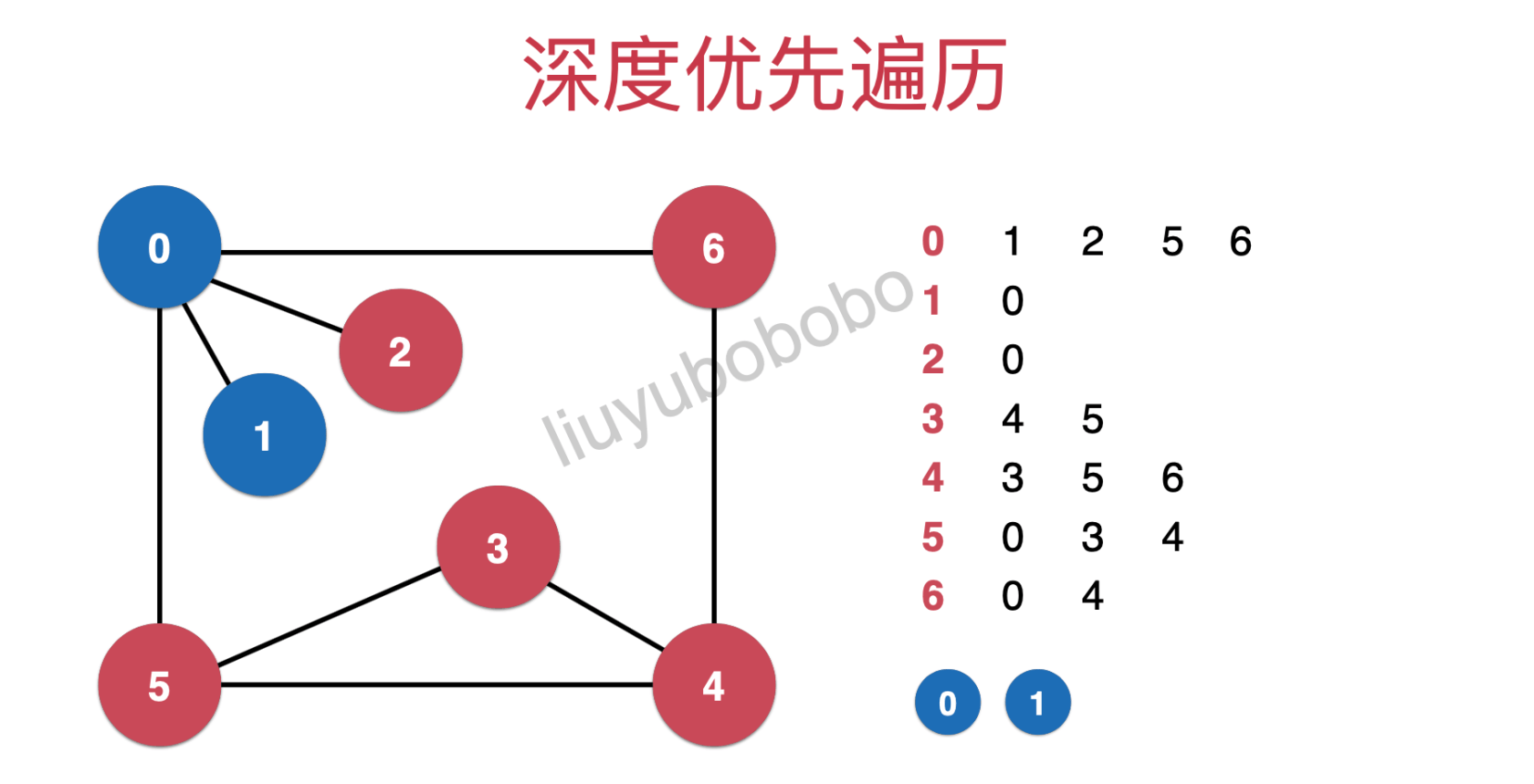
遍历第1行时,第1行后续只有0(0已被遍历然后返回第0行),所以开始遍历2(同时遍历方向也向第2行)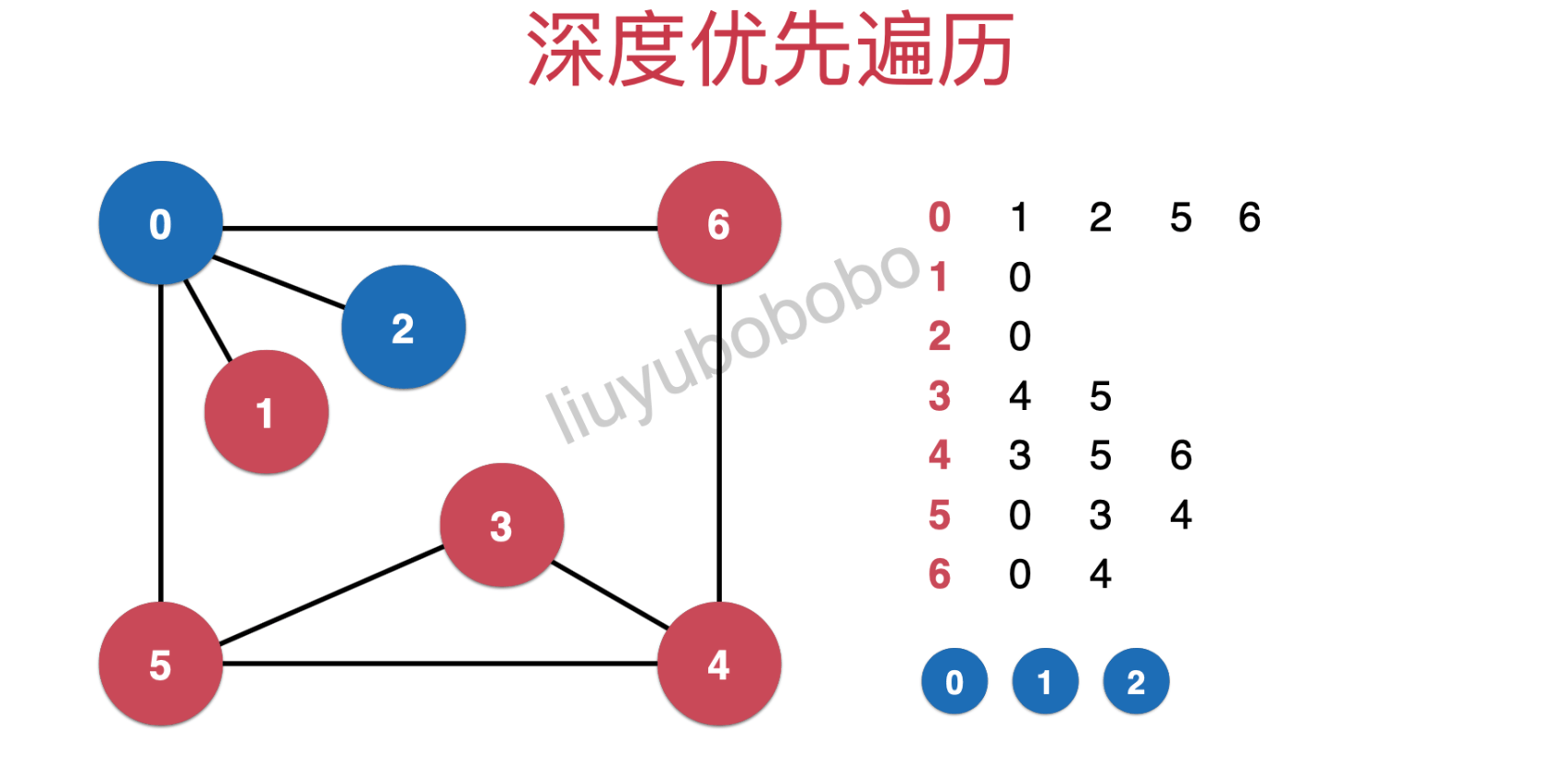
同理
返回到了第0行,遍历5,同时遍历方向变成了第5行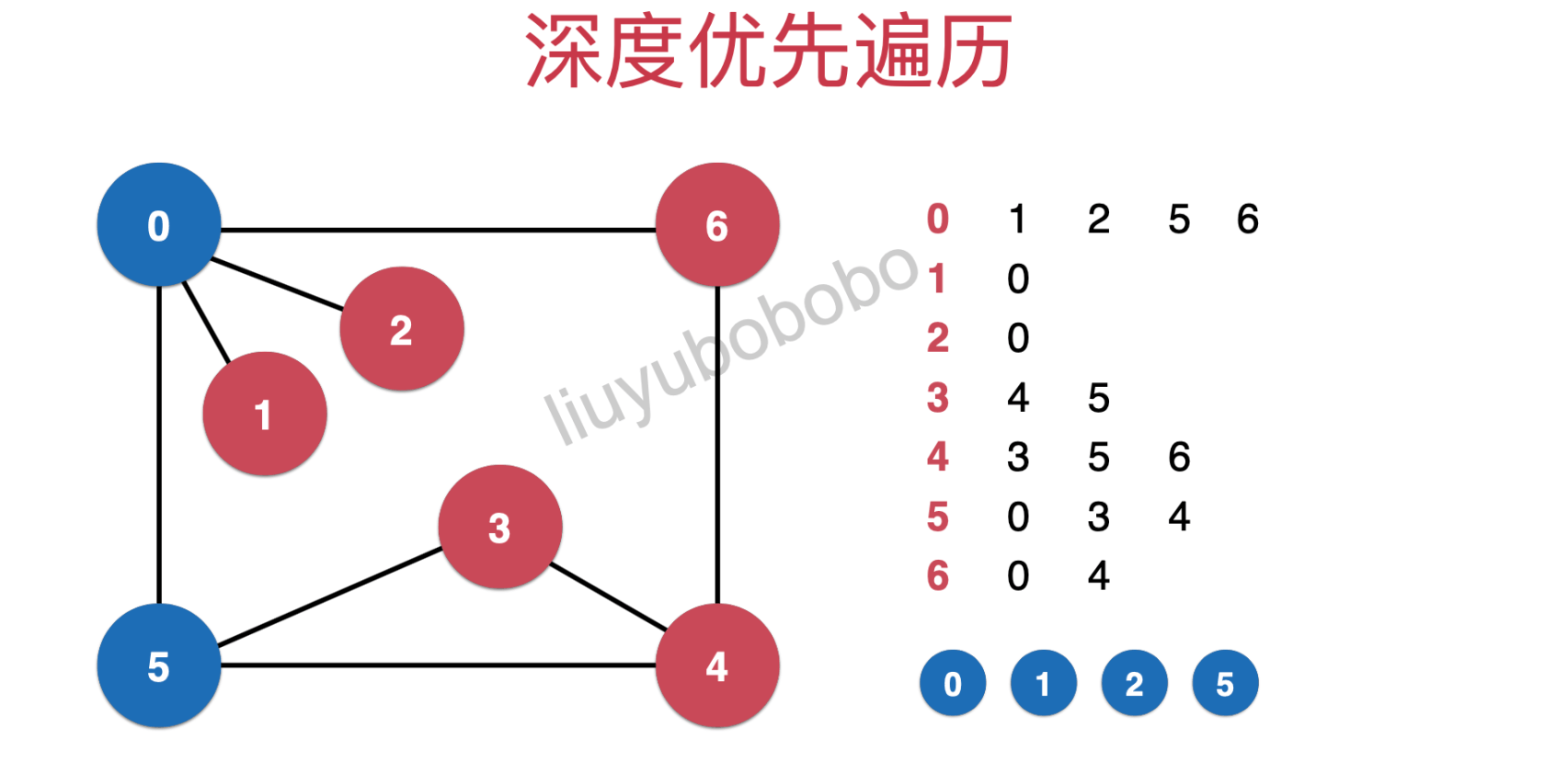
第5行的后续第一个节点是0(已被遍历),接着往后走就是节点3
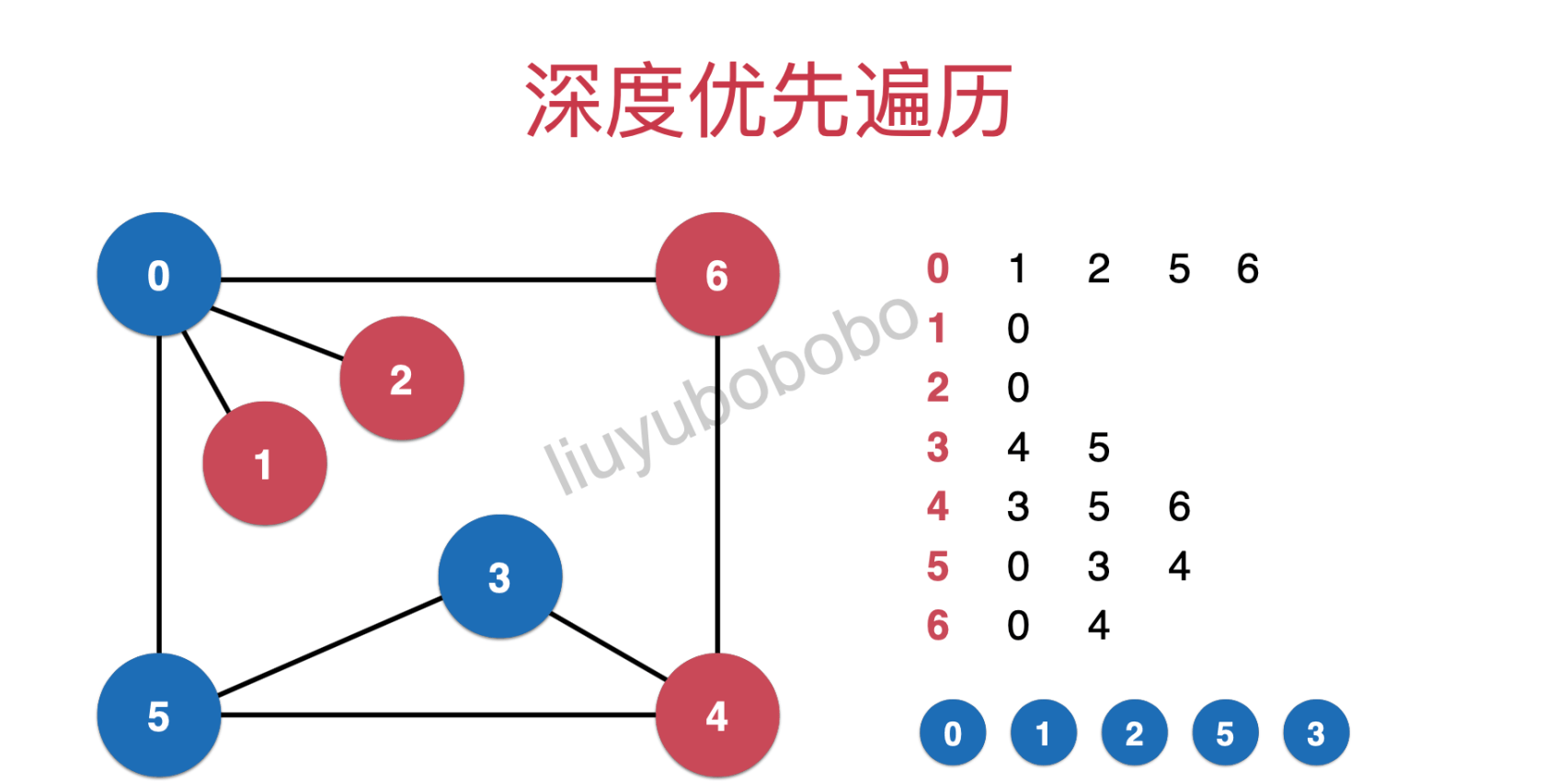
遍历完节点3后,看第3行的后续是节点4,遍历节点4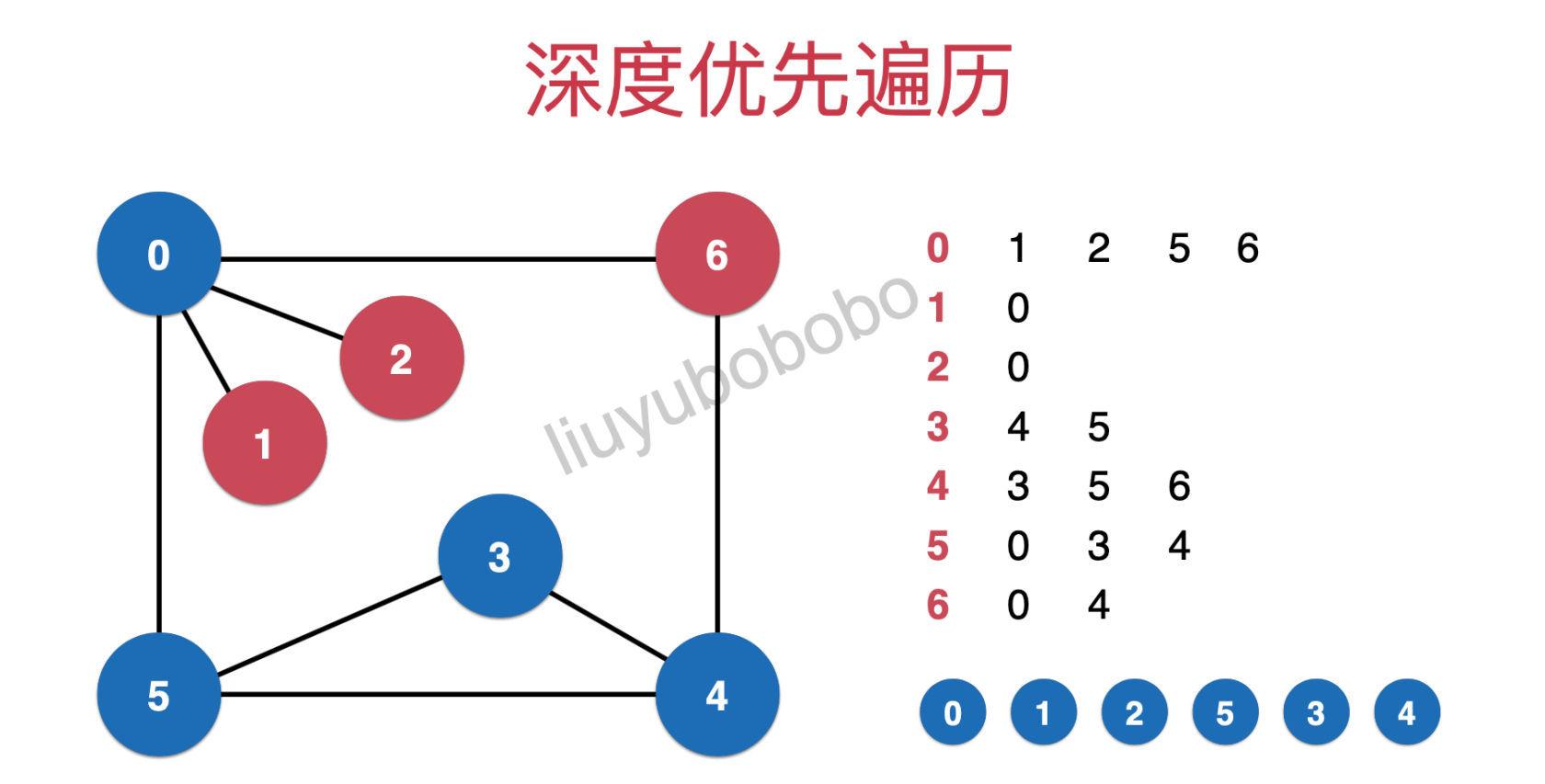
同理现在就该遍历6了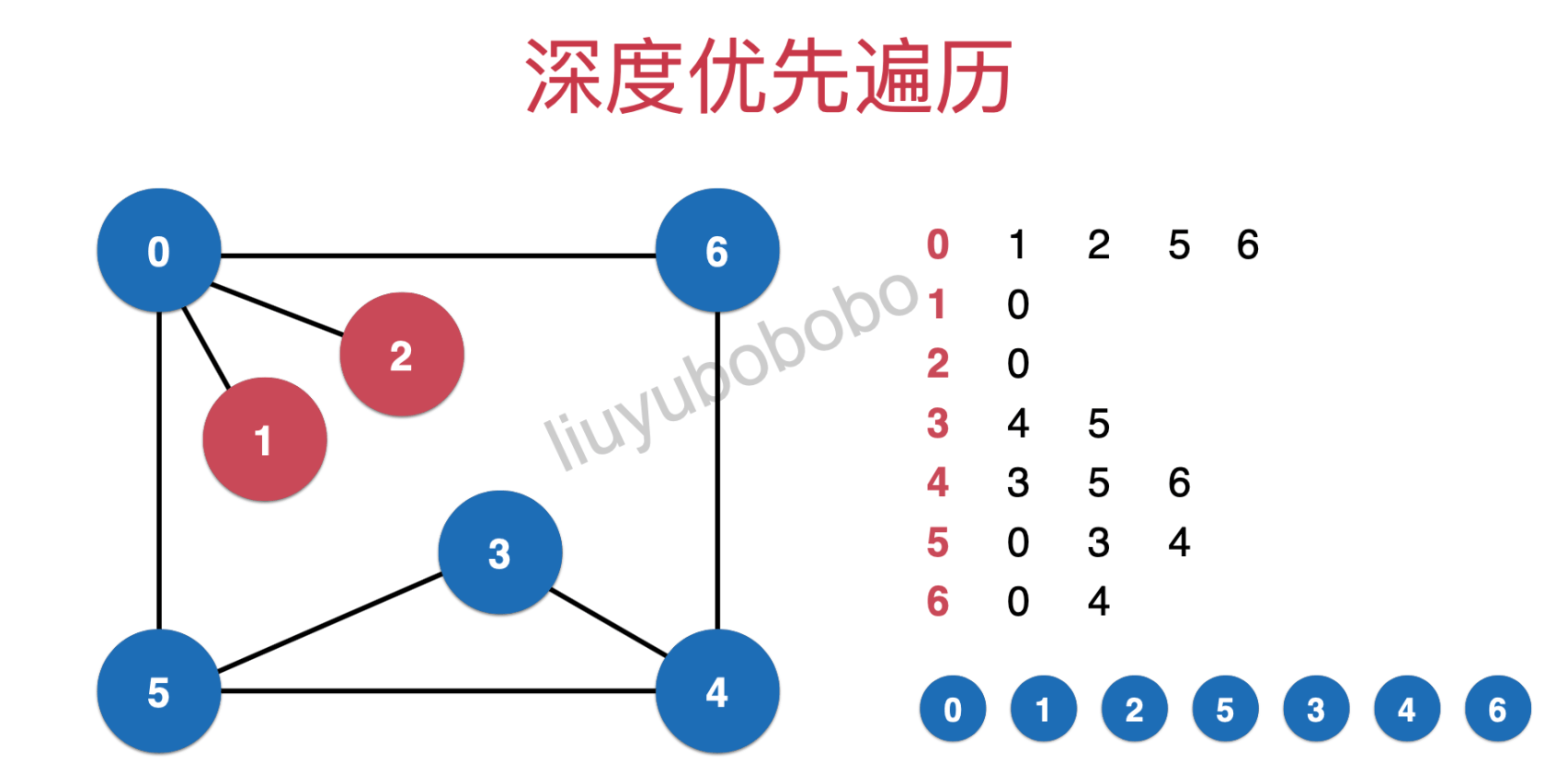
至此图的遍历就完成了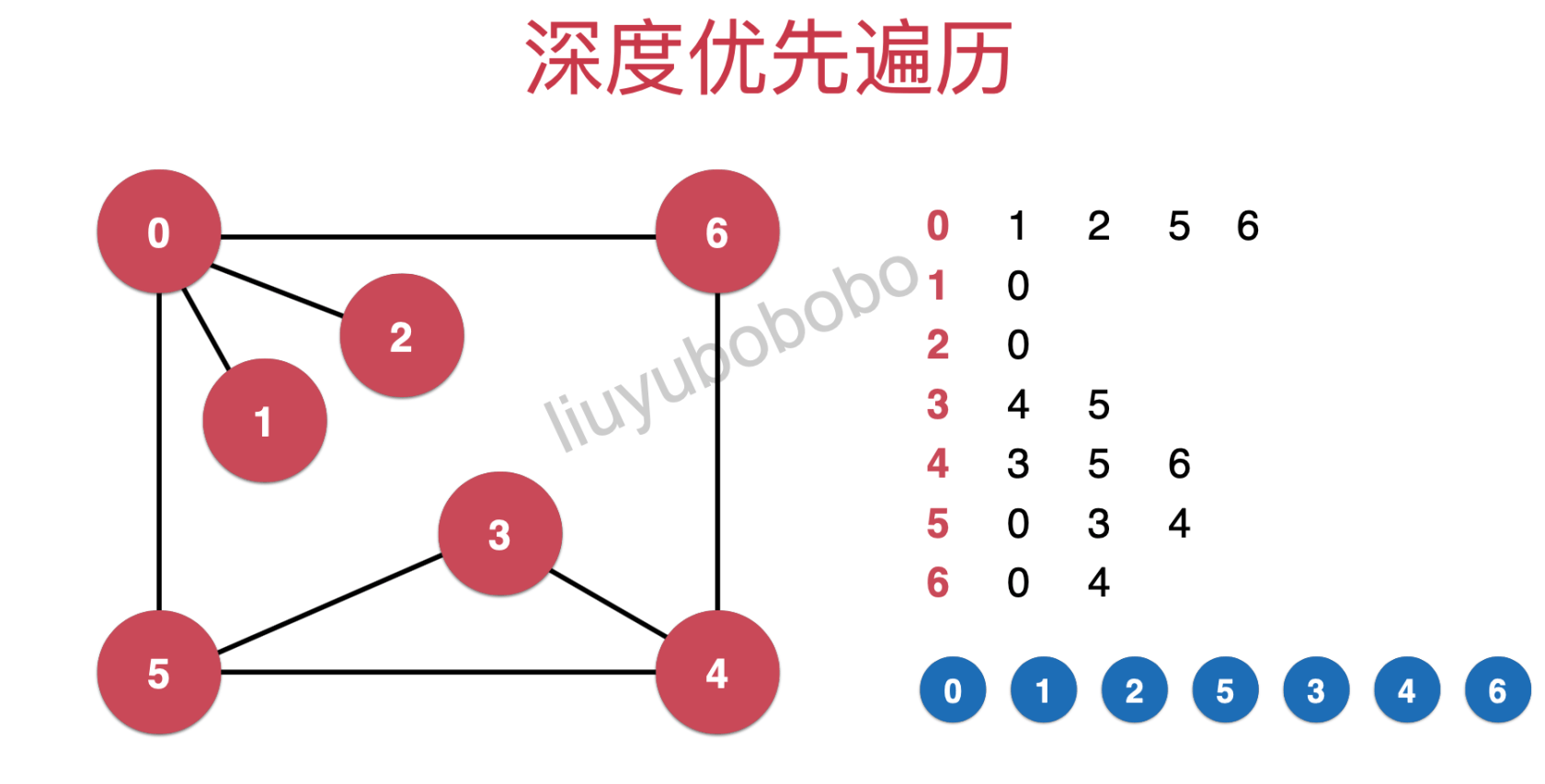
三、代码实现
#include <iostream>
#include <cassert>
using namespace std;
//求无权图的联通分量
template <typename Graph>
class Component{
private:
Graph &G; //图的引用
bool *visited; //记录深度遍历已经被访问过的节点
int ccount; //记录联通分量
int *id; //每个节点对应的联通分量
//dfs遍历
void dfs(int v){
visited[v] = true;
id[v] = ccount;
//传入迭代器
typename Graph::adjIterator adj(G, v);
for(int i = adj.begin(); !adj.end(); i = adj.next()){
if(!visited[i]){
dfs(i);
}
}
}
public:
//构造函数,求无权图的联通分量
Component(Graph &graph):G(graph){
//算法初始化
id = new int[G.V()];
visited = new bool[G.v()];
ccount = 0;
for(int i = 0; i < G.v(); i++){
visited[i] = false;
id[i] = -1;
}
for(int i = 0; i < G.v(); i++){ //对子图的遍历
//如果visited[i]没有被访问过
if(!visited[i]){
dfs(i);
ccount ++;
}
}
}
//析构函数
~Component(){
delete[] visited;
delete[] id;
}
//返回图的联通分量
int count(){
return ccount;
}
//查询v和w是否联通
bool isComponent(int v, int w){
assert( v >= 0 && v < G.V() );
assert( w >= 0 && w < G.V() );
return id[v] = id[w];
}
};
本作品采用《CC 协议》,转载必须注明作者和本文链接



 关于 LearnKu
关于 LearnKu



