2022-09-09：给定一个正整数 n，返回 连续正整数满足所有数字之和为 n 的组数

2022-09-09：给定一个正整数 n，返回 连续正整数满足所有数字之和为 n 的组数 。
示例 1:
输入: n = 5
输出: 2
解释: 5 = 2 + 3，共有两组连续整数([5],[2,3])求和后为 5。
示例 2:
输入: n = 9
输出: 3
解释: 9 = 4 + 5 = 2 + 3 + 4
示例 3:
输入: n = 15
输出: 4
解释: 15 = 8 + 7 = 4 + 5 + 6 = 1 + 2 + 3 + 4 + 5

答案2022-09-09：

如果有，N = (x+1) + (x+2) + … + (x+k)
上式子可以化简为：N = kx + k(k+1)/2
左右两边同时乘以2，可以得到：2N = 2kx + k^2 + k
进而得到：2N = k(2x + k + 1)
2N 偶 k * (2x + k + 1)
k 2x + k + 1
所以，对于2N = k(2x + k + 1)，这个式子来说，只要给定不同的一组x和k，就对应一种不同的方案
进一步分析可以看出：
如果k为偶数，那么2x + k + 1就是奇数
如果k为奇数，那么2x + k + 1就是偶数
2N = 左 K 右 2x + k + 1
2N 奇数因子K, 2x + k + 1
也就是说，对于每一种方案，k和2x + k + 1，一定是不同的，并且连奇偶性都相反
所以2N里任何一个奇数因子，可能作为k这一项，也可能作为2x+k+1这一项，
不管奇数因子作为哪一项，都可以推出另外一项的值，进而确定k和x具体是多少
进而可以推出，2N里有多少个奇数因子，就有多少种方案
于是这个题就变成了求N里有多少奇数因子
一般来说，求N里有多少奇数因子，用O(根号N)的方法肯定可以
但其实可以更加的优化，
如果 N = 3^a * 5^b * 7^c * 9^d ….那么N一共会出现多少奇数因子呢？
N的质数因子：可以选择0个3..可以选择1个3…可以选择2个3…可以选择a个3，所以有a+1种选择
上面的选择，去乘以：可以选择0个5..可以选择1个5…可以选择2个5…可以选择b个5，所以有b+1种选择
上面的选择，去乘以：可以选择0个7..可以选择1个7…可以选择2个7…可以选择c个7，所以有c+1种选择
…
所以，一共有(a + 1) * (b + 1) * (c + 1) * (d + 1) …..这么多个奇数因子。

代码用rust编写。代码如下：

fn main() {
    let n = 3 * 5 * 7;
    let ans = consecutive_numbers_sum1(n);
    println!("ans = {}", ans);
    let ans = consecutive_numbers_sum2(n);
    println!("ans = {}", ans);
}

fn consecutive_numbers_sum1(mut n: i32) -> i32 {
    while (n & 1) == 0 {
        n >>= 1;
    }
    let mut res = 1;
    let mut i = 3;
    while i <= n {
        let mut count = 1;
        while n % i == 0 {
            n /= i;
            count += 1;
        }
        res *= count;
        i += 2
    }
    return res;
}

// 进一步优化
fn consecutive_numbers_sum2(mut n: i32) -> i32 {
    while (n & 1) == 0 {
        n >>= 1;
    }
    let mut res = 1;
    // O(根号N)
    let mut i = 3;
    while i * i <= n {
        let mut count = 1;
        while n % i == 0 {
            n /= i;
            count += 1;
        }
        // rest *= （计数+1）
        res *= count;
        i += 2
    }
    // N == 1表示已经找到了所有奇数因子
    // N != 1表示只残留着最后一个奇数因子了
    // 简单证明：如果N最后残留着不只一个奇数因子，
    // 比如x*y(不妨设x<y)，那么在for循环里，就依然会有i*i <= N
    // 因为i=x时，x*x <= x*y,所以x在for循环里就能计算到
    // 所以如果N != 1表示只残留着一个奇数因子
    return if n == 1 { res } else { res << 1 };
}

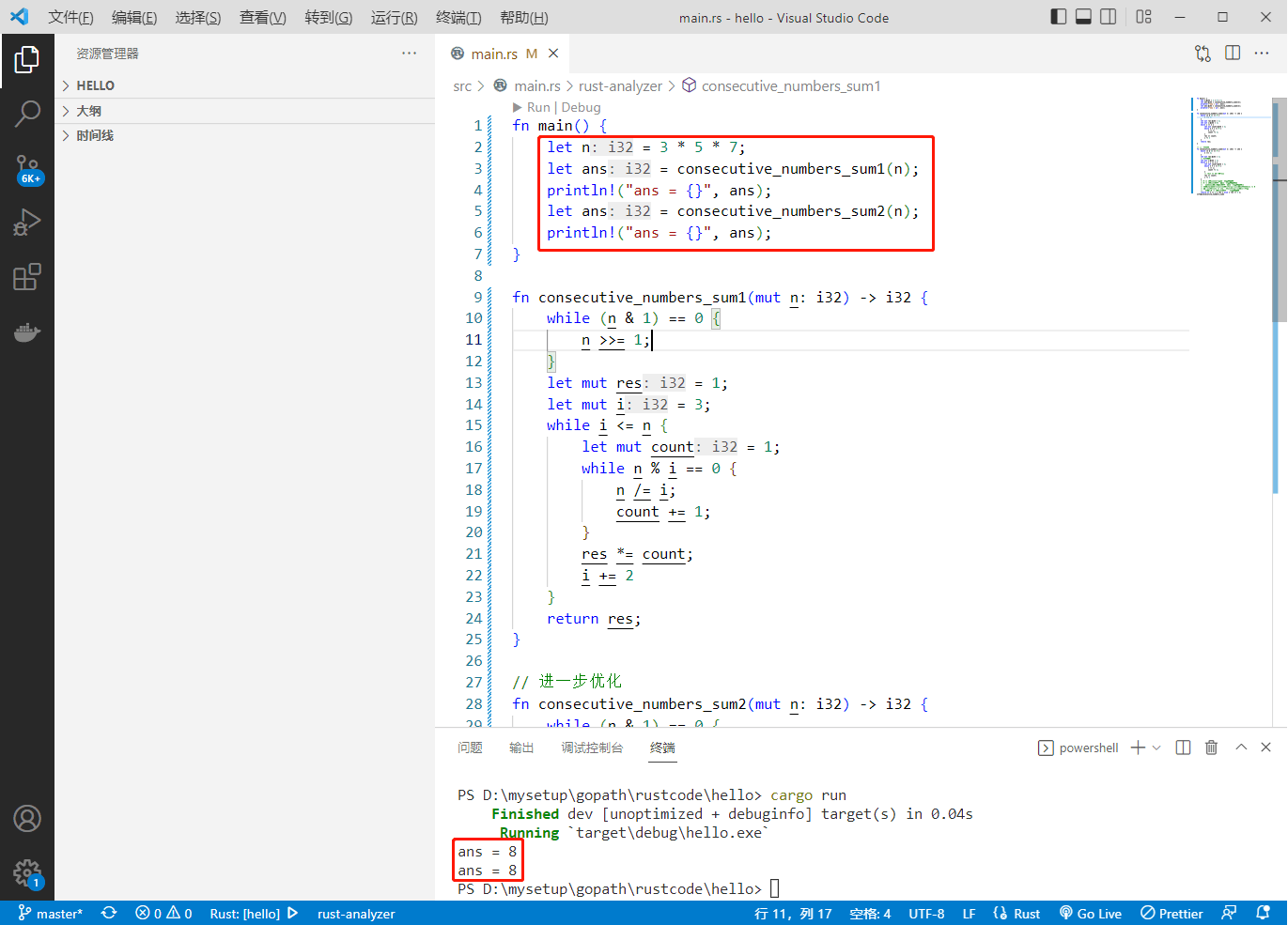
执行结果如下：

左神java代码

本作品采用《CC 协议》，转载必须注明作者和本文链接