Go 小白理念02-时间复杂度
算法的时间复杂度
定义： 事前预估算法时间开销T(n)与问题规模n的关系（T表示“time”）
规则：
问题： T(n) = 3n + 3 (这个表达式如何简化？)
= O(n)
- 加法规则：T(n) = T1(n) + T2(n) = O(f(n)) + O(g(n)) = O(max(f(n), g(n))) （多项相加，只保留最高阶的项，且系数变为1）
- 乘法规则：T(n) = T1(n)×T2(n) = O(f(n))×O(g(n)) = O(f(n)×g(n))（多项相乘，都保留 ）
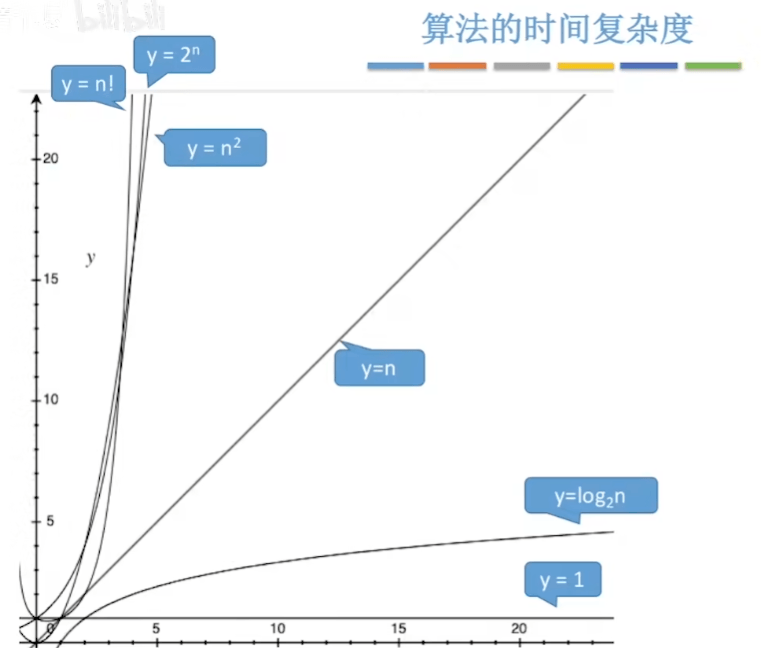
- 算法好坏：O(1) < O(log2n) < O(n) < O(nlog2n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)（口诀：常对幂指阶）
问题： 代码很长，如何算复杂度？
结论
- 顺序执行的代码，常数项可以被忽略
- 只需挑循环中的一个基本操作分析它的执行次数与 n 的关系即可
- 如果有多层嵌套循环，只需关注最深层循环，循环了几次
其他
- 数量级仅需考虑循环内，最深层嵌套的部分
- 最坏时间复杂度：最坏情况下算法的时间复杂度
- 平均时间复杂度：所有输入示例等概率出现的情况下，算法的期望运行时间
- 最好时间复杂度：最好情况下算法的时间复杂度
- 一般只考虑最坏和平均复杂度
关于 LearnKu
粤公网安备 44030502004330号