机器学习基础(三)
逻辑回归
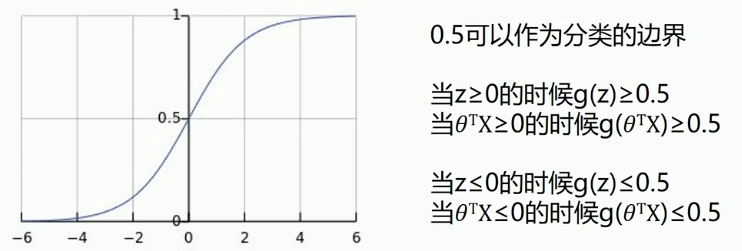
逻辑回归方程
可以根据改图进行分类
代价函数
正则化代价函数
求导过程
拟合程度标准
- 正确率:正确数量 / 所得数量
- 召回率:所的数量 / 样本的总正确数量
- F1值:正确率 * 召回率 * 2 / (正确率 + 召回率)
F-Score是最常用的解决正确率和召回率矛盾的方法,当β=1时,即为F1值
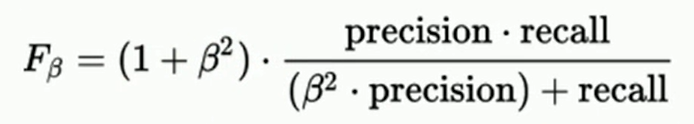
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
data = np.genfromtxt('E:/project/python/data/csv/LR-testSet.csv', delimiter=',')
x_data = data[:, :-1]
y_data = data[:, -1]
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
for i in range(len(x_data)):
if y_data[i] == 0:
x0.append(x_data[i, 0])
y0.append(x_data[i, 1])
else:
x1.append(x_data[i, 0])
y1.append(x_data[i, 1])
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)
plot()
x_test = np.array([[-4], [3]])
y_test = (-logistic.intercept_ - x_test * logistic.coef_[0][0]) / logistic.coef_[0][1]
plt.plot(x_test, y_test, 'k')
plt.show()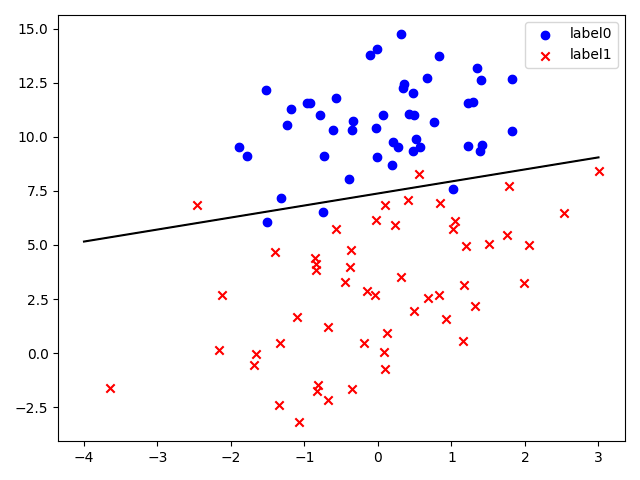
本作品采用《CC 协议》,转载必须注明作者和本文链接

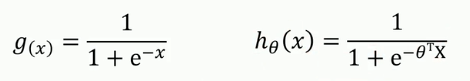
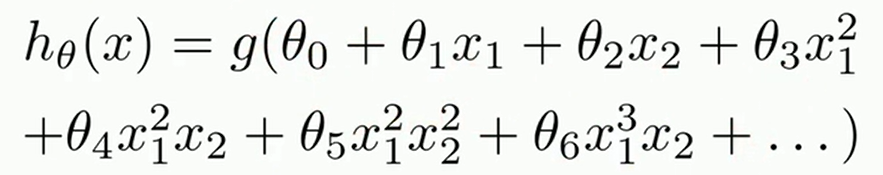
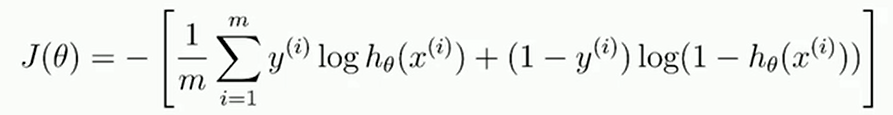
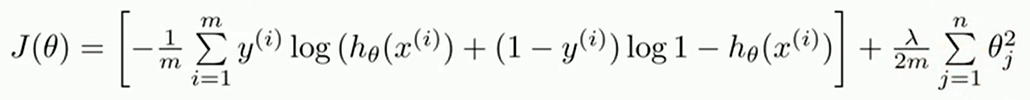
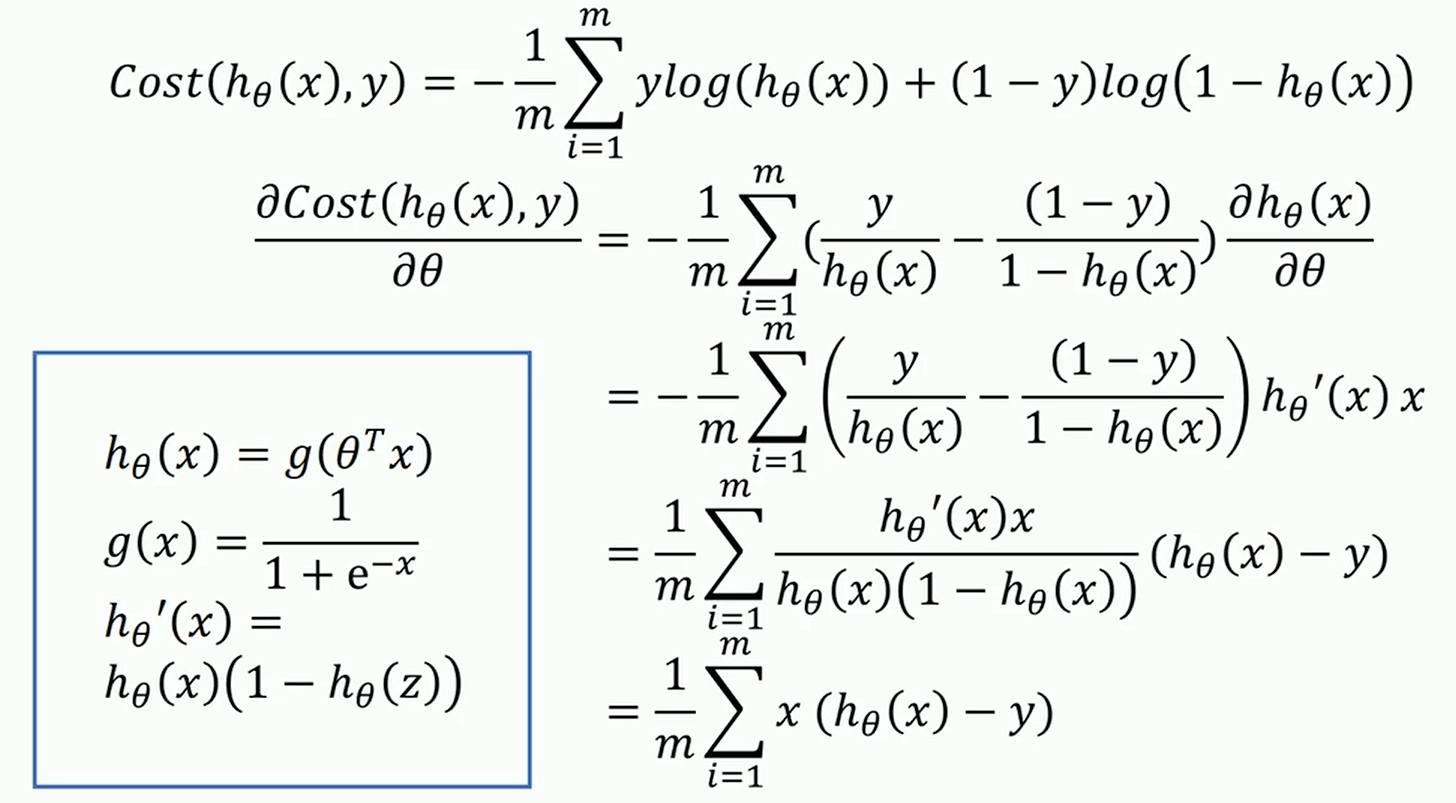


 关于 LearnKu
关于 LearnKu



