决策树
什么是决策树
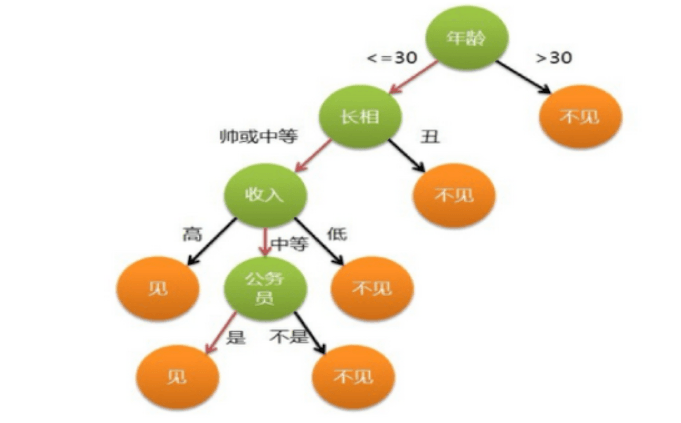
决策树是一种机器学习的方法,决策树是一种树形结构,其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果。
熵
熵 Entropy 是 “混乱” 程度的量度。
系统越有序,熵值越低;系统越混乱或者分散,熵值越高。
假如事件A的分类划分是(A1,A2,…,An),每部分发生的概率是(p1,p2,…,pn),那信息熵定义为公式如下:
Ent(A)=- \sum {k=1}^{n}p{k} \log {2}p{k}
=-p_{1} \log {2}p{1}-p_{2} \log {2}p{2}- \cdots -p_{n} \log {2}p{n}
篮球比赛里,有4个球队 {A,B,C,D} ,获胜概率分别为{1/2, 1/4, 1/8, 1/8},求H(X)
信息熵 H(X) = 1\2log(2)+1\4log(4)+1\8log(8)+1\8log(8)=(1\2+1\2+3\8+3\8)log(2)=7\4
决策树的划分依据
信息增益
信息增益 = entroy(前) - entroy(后)
特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差,即公式为:
g(D,A)=H(D)-H(D|A)
信息熵的计算:
H(D)=- \sum {k=1}^{K} \frac{|C{k}|}{|D|} \log \frac{|C_{k}|}{|D|} 注:C_k 表示属于某个类别的样本数
条件熵的计算:
H(D|A)=-\sum {i=1}^{n} \frac{|D{i}|}{|D|} \sum {k=1}^{K} \frac{|D{ik}|}{|D_{i}|} \log \frac{|D_{ik}|}{|D_{i}|}
信息增益率(略)
基尼值和基尼指数
基尼值Gini(D):从数据集D中随机抽取两个样本,其类别标记不一致的概率。Gini(D)值越小,数据集D的纯度越高。
Gini(D)= \sum {k=1}^{|y|} \sum _{k^{ \prime } \neq k}p{k}p_{k^{ \prime }}=1- \sum {k=1}^{|y|}p{k}^{2}
基尼指数Gini_index(D):一般,选择使划分后基尼系数最小的属性作为最优化分属性。
Gini_{-}index(D,a)= \sum _{ \nu =1}^{V} \frac{|D^{ \nu }|}{|D|}Gini(D^{ \nu })
决策树构建
基本步骤
- 开始将所有记录看作一个节点
- 遍历每个变量的每一种分割方式,找到最好的分割点
- 分割成两个节点N1和N2
- 对N1和N2分别继续执行2-3步,直到每个节点足够“纯”为止。
变量划分
- 数字型:变量类型是整数或浮点数,用“>=”,“>”,“<”或“<=”作为分割条件。
- 名称型(Nominal):变量只能从有限的选项中选取,使用“=”来分割。
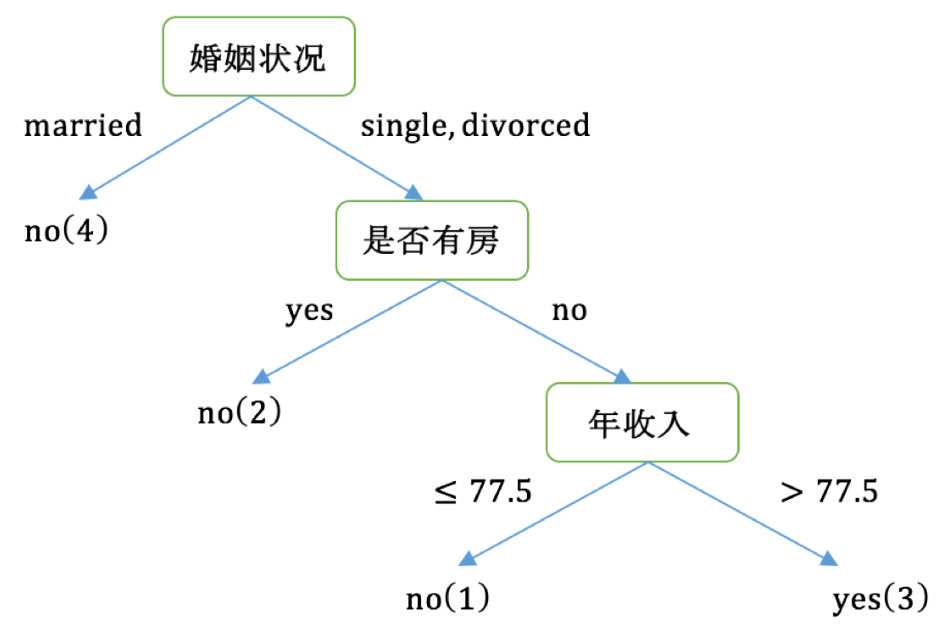
例子:请根据下图列表,按照基尼指数的划分依据,做出决策树。
| 序号 | 是否有房 | 婚姻状况 | 年收入 | 是否拖欠贷款 |
|---|---|---|---|---|
| 1 | yes | single | 125K | no |
| 2 | no | married | 100K | no |
| 3 | no | single | 70K | no |
| 4 | yes | married | 120K | no |
| 5 | no | divorced | 95K | yes |
| 6 | no | married | 60K | no |
| 7 | yes | divorced | 220K | no |
| 8 | no | single | 85K | yes |
| 9 | no | married | 75K | no |
| 10 | no | single | 90K | yes |
对数据集非类标号属性{是否有房,婚姻状况,年收入}分别计算它们的Gini系数增益,取Gini系数增益值最大的属性作为决策树的根节点属性。
根节点的Gini系数为:Gini(是否拖欠货款)=1-( \frac{3}{10})^{2}-( \frac{7}{10})^{2}=0.42
当根据是否有房来进行划分时,Gini系数增益计算过程为:
Gini(左子节点)=1-( \frac{0}{3})^{2}-( \frac{3}{3})^{2}=0
Gini(右子节)=1-( \frac{3}{7})^{2}-( \frac{4}{7})^{2}=0.4898
是否有房=0.42- \frac{7}{10} \times 0.4898- \frac{3}{10} \times 0=0.077
| 是否有房 | 是否有房 | ||
|---|---|---|---|
| N1(Yes) | N2(No) | ||
| 是否拖欠贷款 | Yes | 0 | 3 |
| 是否拖欠贷款 | No | 3 | 4 |
按婚姻状况属性来划分,属性婚姻状况有三个可能的取值{married,single,divorced}
分组为{married} | {single,divorced}时:
=0.42- \frac{4}{10} \times 0- \frac{6}{10} \times \left[ 1-( \frac{3}{6})^{2}-( \frac{3}{6})^{2} \right]=0.12
当分组为{divorced} | {single,married}时:
=0.42- \frac{2}{10} \times 0.5- \frac{8}{10} \times \left[ 1-( \frac{2}{8})^{2}-( \frac{6}{8})^{2} \right]=0.02
当分组为{single} | {married,divorced}时:
=0.42- \frac{4}{10} \times 0.5- \frac{6}{10} \times \left[ 1-( \frac{1}{6})^{2}-( \frac{5}{6})^{2} \right]=0.053
对比计算结果,根据婚姻状况属性来划分根节点时取Gini系数增益最大的分组作为划分结果,即:{married} | {single,divorced}
对于年收入属性为数值型属性,首先需要对数据升序排序,然后从小到大依次用相邻值的中间值作为分隔将样本划分为两组。

例如节点为65时: Gini(年收入)=0.42- \frac{1}{10} \times 0- \frac{9}{10} \times \left[ 1-( \frac{6}{9})^{2}-( \frac{3}{9})^{2} \right] =0.02
根据计算知道,三个属性划分根节点的增益最大的有两个:年收入属性和婚姻状况,他们的增益都为0.12。此时,选取首先出现的属性作为第一次划分。接下来,采用同样的方法,分别计算剩下属性。
去掉married的数据
Gini(是否拖欠货)=1-( \frac{3}{6})^{2}-( \frac{3}{6})^{2}=0.5
对于是否有房属性,可得:Gini(是否有房)=0.5- \frac{4}{6} \times \left[ 1-( \frac{3}{4})^{2}-( \frac{1}{4})^{2} \right] - \frac{2}{6} \times 0=0.25
对于年收入属性则有:

常见决策树
信息熵:Ent(D)=- \sum {i=1}^{k}p{i} \cdot \log (p_{i})
信息增益:Gain(D,a)=Ent(D)- \sum {i}^{k}p{i} \times Ent(D|i)(ID3决策树)
信息增益率:Gain_{-}ratio(D,a)= \frac{Gain(D,a)}{Ent(a)}(C4.5决策树)
基尼值:Gini(D)=1- \sum {i=1}^{k}p{i} \cdot p_{i}
基尼指数:Giniindex(D|a)= \sum {i=1}^{k}p{i} \cdot Gini(D|i)(CART决策树)

 从0开始学AI
从0开始学AI

 关于 LearnKu
关于 LearnKu



