支持向量机(SVM)
参考文章:支持向量机(SVM)——原理篇 - 知乎 (zhihu.com)
算法原理
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器。
SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。

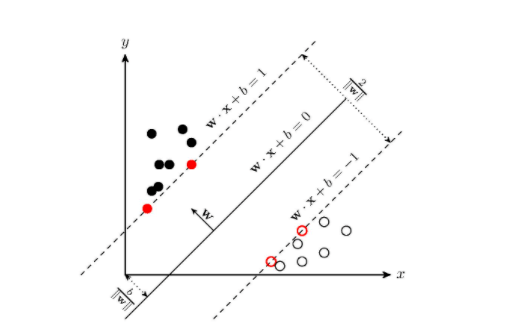
几何间隔: 对于给定的数据集 T 和超平面 w \cdot x+b=0 , 定义超平面关于样本点 \left(x_{i}, y_{i}\right) 的几何间隔为
\gamma_{i}=y_{i}\left(\frac{\boldsymbol{w}}{|\boldsymbol{w}|} \cdot \boldsymbol{x}_{\boldsymbol{i}}+\frac{b}{|\boldsymbol{w}|}\right)
根据以上定义,SVM模型的求解最大分割超平面问题可以表示为以下约束最优化问题:
\max _{\boldsymbol{w}, b} \boldsymbol{\gamma}
s.t. \quad y_{i}\left(\frac{\boldsymbol{w}}{|\boldsymbol{w}|} \cdot \boldsymbol{x}_{i}+\frac{b}{|\boldsymbol{w}|}\right) \geq \gamma, i=1,2, \ldots, N
将约束条件两边同时除以{\gamma},得到
y_{i}\left(\frac{\boldsymbol{w}}{|\boldsymbol{w}| \gamma} \cdot \boldsymbol{x}_{i}+\frac{b}{|\boldsymbol{w}| \gamma}\right) \geq 1
因为 |\boldsymbol{w}|, \quad \gamma 都是标量, 所以为了表达式简洁起见, 令
\boldsymbol{w}=\frac{\boldsymbol{w}}{|\boldsymbol{w}| \gamma}
b=\frac{b}{|\boldsymbol{w}| \gamma}
又因为最大化 \gamma, 等价于最大化 \frac{1}{|\boldsymbol{w}|}, 也就等价于最小化 \frac{1}{2}|\boldsymbol{w}|^{2} \quad\left(\frac{1}{2}\right. 是为了后面求导以后形式简洁, 不影响结果),
因此SVM模型的求解最大分割超平面问题又可以表示为以下约束 最优化问题
\min_{w, b} \frac{1}{2}|\boldsymbol{w}|^{2}
s.t. y_{i}\left(\boldsymbol{w} \cdot \boldsymbol{x}_{i} + b\right) \geq 1, i=1,2, \ldots, N
求解出 w 和 b,进而求得我们最初的目的:找到超平面,即”决策平面”。
\boldsymbol{w}^{}=\sum_{i=1}^{N} \alpha_{i}^{} y_{i} \boldsymbol{x}{i}
b^{*}=y{j}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(\boldsymbol{x}{i} \cdot \boldsymbol{x}{j}\right)
到这里都是基于训练集数据线性可分的假设下进行的,但是实际情况下几乎不存在完全线性可分的数据,为了解决这个问题,引入了“软间隔”的概念。采用hinge损失,将原优化问题改写为
\min {\boldsymbol{w}, b, \xi{i}} \frac{1}{2}|\boldsymbol{w}|^{2}+C \sum_{i=1}^{m} \xi_{i}
s.t. \quad y_{i}\left(\boldsymbol{w} \cdot \boldsymbol{x}{i}+b\right) \geq 1-\xi{i} \xi_{i} \geq 0, i=1,2, \ldots, N

ski-learn代码
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
iris = datasets.load_iris()
x = iris.data
y = iris.target
X = x[y < 2, :2]
y = y[y < 2]
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(X)
X_s = ss.transform(X)
# 引入线性
from sklearn.svm import LinearSVC
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
svc = LinearSVC(C=1e9)
svc.fit(X_s, y)
plot_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_s[y==0,0], X_s[y==0,1])
plt.scatter(X_s[y==1,0], X_s[y==1,1])
plt.show()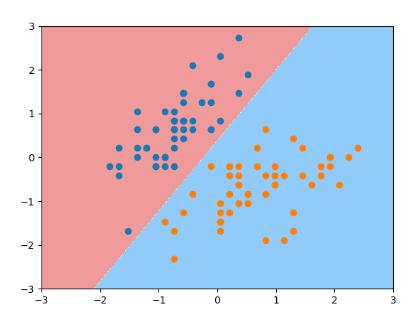
非线性SVM算法原理
对于输入空间中的非线性分类问题,可以通过非线性变换将它转化为某个维特征空间中的线性分类问题,在高维特征空间中学习线性支持向量机。目标函数和分类决策函数都只涉及实例和实例之间的内积,所以不需要显式地指定非线性变换,而是用核函数替换当中的内积。
核函数表示,通过一个非线性转换后的两个实例间的内积。
输入空间中的 x, z, 有
K(x, z)=\phi(x) \cdot \phi(z)
用核函数 替代内积,求解得到的就是非线性支持向量机
\begin{aligned}
&\text { 多项式核函数 } \quad K(x, y)=(x \cdot y+c)^{d}\
&\text { 线性核函数 } \quad K(x, y)=x \cdot y
\end{aligned}
使用多项式核函数的SVM



高斯核函数
RBF Radial Basis Function Kernel
高斯核函数:
K(x, y)=e^{-\gamma|x-y|^{2}}
高斯函数:\quad g(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{\left.-\frac{1}{2} \frac{x-\mu}{\sigma}\right)^{2}}
依靠升维使得原本线性不可分的数据线性可分。RBF Radial Basis Function Kernel



高斯核:对于每一个数据点都是地标点。都要核函数计算。m^{\star} n 的数据映射成了 m^{\star}m 的数据


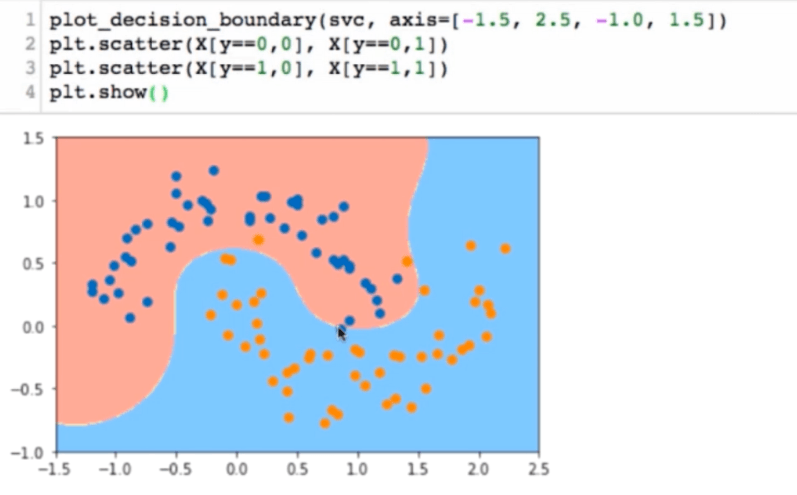
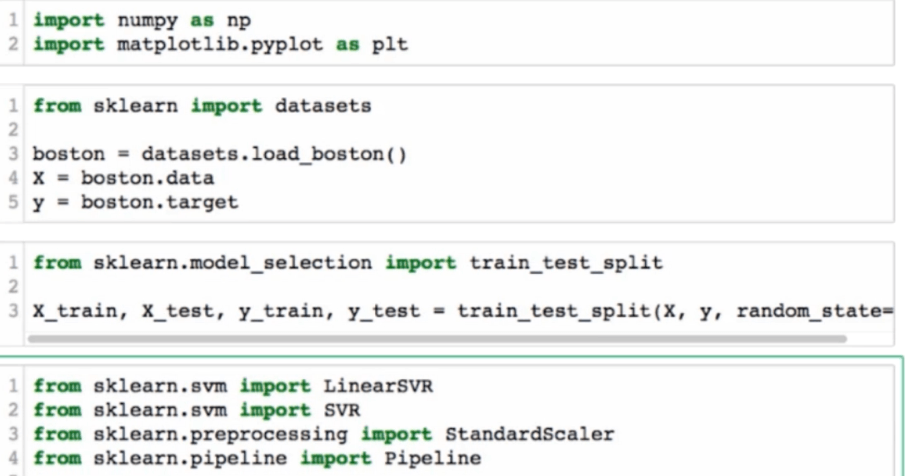
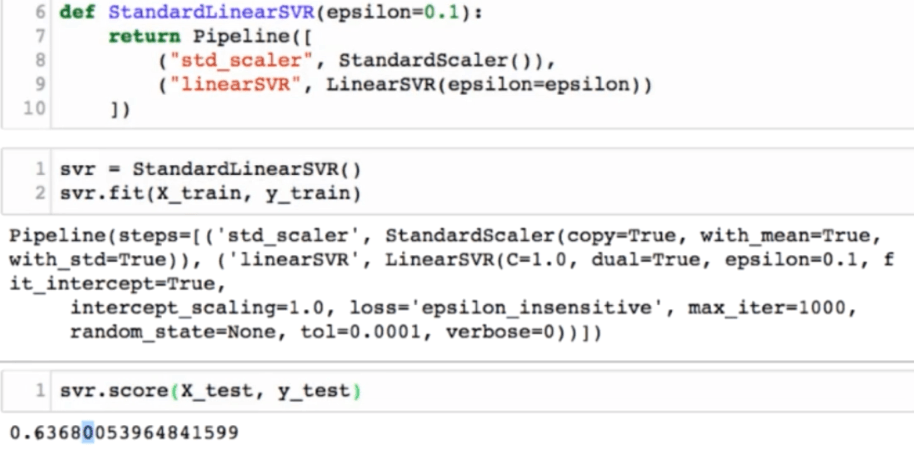
SVM思想解决回归问题

 从0开始学AI
从0开始学AI

 关于 LearnKu
关于 LearnKu



