神经网络
图片基础
组成一张图片特征值是所有的像素值,有三个维度:图片长度、图片宽度、图片通道数。
如果一个像素点,有RGB三种颜色来描述它,就是三通道。
假设一张彩色图片的长200,宽200,通道数为3,那么总的像素数量为200 * 200 * 3
在TensorFlow中如何用张量表示一张图片呢?
一张图片可以被表示成一个3D张量,即其形状为[height, width, channel],height就表示高,width表示宽,channel表示通道数。
我们会经常遇到3D和4D的表示
- 单个图片:[height, width, channel]
- 多个图片:[batch,height, width, channel],batch表示一个批次的张量数量
图片读取
要使用该模块需要下载图片读取库
pip install Pillowimage模块提供了读取图片处理的API
from tensorflow.python.keras.preprocessing.image import load_img, img_to_array
image = load_img("./image/龙猫提莫.png", target_size=(122, 111))
print(image)
image = img_to_array(image)
print(image.shape)<PIL.JpegImagePlugin.JpegImageFile image mode=RGB size=384x256 at 0x10E51D6D8>NHWC与NCHW
在读取设置图片形状的时候有两种格式”channels_first” or “channels_last”.:
设置为 “NHWC” 时,排列顺序为 [batch, height, width, channels];
设置为 “NCHW” 时,排列顺序为 [batch, channels, height, width]。
Tensorflow默认的[height, width, channel]
假设RGB三通道两种格式的区别如下图所示:

所以在读取数据处理形状的时候:
1 image (3072, ) —>tf.reshape(image, [])
里面的shape是[channel, height, width], 所以得先从[depth *height* width] to [depth, height, width]。
2 然后使用tf.transpose, 将刚才的数据[depth, height, width],变成Tensorflow默认的[height, width, channel]
# 1、想要变成:[2 height, 2width, 3channel] In [8]: tf.reshape([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12], [3, 2, 2]).eval() # 接着使用tf.transpose ,0,1,2代表三个维度标记 In [17]: tf.transpose(depth_major, [1, 2, 0]).eval() Out[17]: array([[[ 1, 5, 9], [ 2, 6, 10]], [[ 3, 7, 11], [ 4, 8, 12]]], dtype=int32)
keras 数据集
CIFAR10 小图片分类数据
50000张32x32大小的训练数据和10000张测试数据,总共100个类别。
from keras.datasets import cifar100
(x_train, y_train), (x_test, y_test) = cifar100.load_data()返回两个元组:
- x_train, x_test: uint8 数组表示的 RGB 图像数据,尺寸为 (num_samples, 3, 32, 32) 或 (num_samples, 32, 32, 3),基于
image_data_format后端设定的channels_first或channels_last。 - y_train, y_test: uint8 数组表示的类别标签,尺寸为 (num_samples,)。
时装分类Mnist数据集
60,000张28x28总共10个类别的灰色图片,10,000张用于测试。
from keras.datasets import fashion_mnist
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()返回两个元组:
- x_train, x_test: uint8 数组表示的灰度图像,尺寸为 (num_samples, 28, 28)。
- y_train, y_test: uint8 数组表示的数字标签(范围在 0-9 之间的整数),尺寸为 (num_samples,)。
神经网络原理
神经网络的主要用途在于分类。

神经网络解决多分类问题最常用的方法是设置n个输出节点,其中n为类别的个数。
softmax回归
Softmax回归将神经网络输出转换成概率结果:
\operatorname{softmax}(y){i}=\frac{e^{y{i}}}{\sum_{j=1}^{n} e^{y_{j}}}
这样就把神经网络的输出也变成了一个概率输出:

那么如何去衡量神经网络预测的概率分布和真实答案的概率分布之间的距离?
交叉熵损失
H_{y^{\prime}}(y)=-\sum_{i} y_{i}^{\prime} \log \left(y_{i}\right)
为了能够衡量距离,目标值需要进行one-hot编码,能与概率值对应,如下图:

如何计算?
0log(0.10)+0log(0.05)+0log(0.15)+0log(0.10)+0log(0.05)+0log(0.20)+1log(0.10)+0log(0.05)+0log(0.10)+0log(0.10)神经网络最后的损失为平均每个样本的损失大小。对所有样本的损失求和取其平均值。
梯度下降算法
成本函数 J 是一个凸函数(只有一个局部最低点),参数w和b的更新公式为:
w:=w-\alpha \frac{d J(w, b)}{d w}, b:=b-\alpha \frac{d J(w, b)}{d b}
注:其中 α 表示学习速率。
Tensorflow实现神经网络
import tensorflow as tf
from tensorflow import kerasSequential模型
- Flatten:将输入数据进行形状改变展开
- Dense:添加一层神经元
- units:神经元个数
- activation:激活函数,参考
tf.nn.relu,tf.nn.softmax,tf.nn.sigmoid - **kwargs:输入上层输入的形状,input_shape=()
tf.keras.Sequential构建类似管道的模型
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation=tf.nn.relu),
keras.layers.Dense(10, activation=tf.nn.softmax)
])Model类型
from keras.models import Model
from keras.layers import Input, Dense
data = Input(shape=(784,))
out = Dense(32)(data)
model = Model(input=data, output=out)Models属性
model.layers:获取模型结构列表model.inputs是模型的输入张量列表model.outputs是模型的输出张量列表model.summary()打印模型的摘要表示
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) (None, 784) 0
_________________________________________________________________
dense (Dense) (None, 64) 50240
_________________________________________________________________
dense_1 (Dense) (None, 128) 8320
_________________________________________________________________
dense_2 (Dense) (None, 10) 1290
=================================================================
Total params: 59,850
Trainable params: 59,850
Non-trainable params: 0Models方法
model.compile(optimizer,loss=None,metrics=None):配置训练相关参数- optimizer:梯度下降优化器
- loss=None:损失类型
- metrics=None, [‘accuracy’]
例如:
model.compile(optimizer=tf.keras.optimizers.Adam(),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# sparse_categorical_crossentropy:对于目标值是整型的进行交叉熵损失计算
# categorical_crossentropy:对于两个output tensor and a target tensor进行交叉熵损失计算model.fit(x=None,y=None, batch_size=None,epochs=1,callbacks=None):进行训练- x:特征值
- y:目标值
- batch_size=None:批次大小
- epochs=1:训练迭代次数
- callbacks=None:添加回调列表(用于如tensorboard显示等)
例如:
model.fit(train_images, train_labels, epochs=5, batch_size=32)model.evaluate(test_images, test_labels)评估模型,不输出预测结果
loss,accuracy = model.evaluate(X_test,Y_test)model.save_weights(filepath)将模型的权重保存为HDF5文件或者ckpt文件model.load_weights(filepath, by_name=False)从HDF5文件(由其创建save_weights)加载模型的权重。默认情况下,架构预计不会更改。要将权重加载到不同的体系结构(具有一些共同的层),请使用by_name=True仅加载具有相同名称的那些层。model.predict模型预测,输入测试集,输出预测结果
y_pred = model.predict(X_test,batch_size = 1)案例:时装分类
70000 张灰度图像,涵盖 10 个类别。以下图像显示了单件服饰在较低分辨率(28x28 像素)下的效果:

| 标签 | 类别 |
|---|---|
| 0 | T 恤衫/上衣 |
| 1 | 裤子 |
| 2 | 套衫 |
| 3 | 裙子 |
| 4 | 外套 |
| 5 | 凉鞋 |
| 6 | 衬衫 |
| 7 | 运动鞋 |
| 8 | 包包 |
import os
import numpy as np
from tensorflow.python.keras.preprocessing.image import load_img, img_to_array
from tensorflow.python.keras.models import Sequential
from tensorflow.python.keras.layers import Dense, Flatten
import tensorflow as tf
from tensorflow import keras
class SingleNN(object):
def __init__(self):
(self.x_train, self.y_train), (self.x_test, self.y_test) = keras.datasets.fashion_mnist.load_data()
# 数据归一化
self.x_train = self.x_train / 255.0
self.x_test = self.x_test / 255.0
# 建立神经网络模型
model = Sequential([
Flatten(input_shape=(28, 28)),
Dense(128, activation=tf.nn.relu),
Dense(10, activation=tf.nn.softmax) # 10个类别
])
def my_compile(self):
SingleNN.model.compile(optimizer=keras.optimizers.Adam(lr=0.01),
loss=keras.losses.sparse_categorical_crossentropy,
metrics=['accuracy']
)
return None
def fit(self):
# 添加回掉函数记录训练过程
# call = keras.callbacks.ModelCheckpoint(
# filepath='./snn_model/singlenn_{epoch:02d}-{acc:.2f}.h5',
# monitor='acc',
# save_best_only=True,
# save_weights_only=True,
# mode='auto',
# period=1
# )
board=keras.callbacks.TensorBoard(
log_dir='./graph/',
write_graph=True
)
# 训练模型
SingleNN.model.fit(self.x_train, self.y_train, epochs=5, callbacks=[board])
def evaluate(self):
lose, acc = SingleNN.model.evaluate(self.x_test, self.y_test)
print(lose, acc)
def predict(self):
# if os.path.exists("./snn_model/"):
SingleNN.model.load_weights("./snn_model/snn.h5")
p = SingleNN.model.predict(self.x_test)
return p
def main():
snn = SingleNN()
snn.my_compile()
snn.fit()
snn.evaluate()
snn.model.save_weights("./snn_model/snn.h5")
# pr = snn.predict()
# res = np.argmax(pr, axis=1)
# print(res)
if __name__ == "__main__":
main()fit的callbacks
可以使用回调来获取培训期间内部状态和模型统计信息的视图。您可以将回调列表(作为关键字参数callbacks)传递给或类的fit()方法。然后将在训练的每个阶段调用回调的相关方法。
ModelCheckpoint
keras.callbacks.ModelCheckpoint(filepath, monitor='val_loss', save_best_only=False, save_weights_only=False, mode='auto', period=1)
- Save the model after every epoch:每隔多少次迭代保存模型
- filepath: 保存模型字符串
- 如果设置 weights.{epoch:02d}-{val_loss:.2f}.hdf5格式,将会每隔epoch number数量并且将验证集的损失保存在该位置
- 如果设置weights.{epoch:02d}-{val_acc:.2f}.hdf5,将会按照val_acc的值进行保存模型
- monitor: quantity to monitor.设置为’val_acc’或者’val_loss’
- save_best_only: if save_best_only=True, 只保留比上次模型更好的结果
- save_weights_only: if True, 只保存去那种(model.save_weights(filepath)), else the full model is saved (model.save(filepath)).
- mode: one of {auto, min, max}. 如果save_best_only=True, 对于val_acc, 要设置max, 对于val_loss要设置min
- period: 迭代保存checkpoints的间隔
check = ModelCheckpoint('./ckpt/singlenn_{epoch:02d}-{val_acc:.2f}.h5',
monitor='val_acc',
save_best_only=True,
save_weights_only=True,
mode='auto',
period=1)
SingleNN.model.fit(self.train, self.train_label, epochs=5, callbacks=[check])Tensorboard
keras.callbacks.TensorBoard(log_dir='./logs', histogram_freq=0, batch_size=32, write_graph=True)
- log_dir:保存事件文件目录
- histogram_freq=0:计算激活值和模型权重直方图的频率(训练轮数中)。 如果设置成 0 ,直方图不会被计算。
- write_graph=True:是否显示图结构
- write_images=False:是否显示图片
- write_grads=True:是否显示梯度
histogram_freq必须大于0
# 添加tensoboard观察
tensorboard = keras.callbacks.TensorBoard(log_dir='./graph', histogram_freq=1,
write_graph=True, write_images=True)
SingleNN.model.fit(self.train, self.train_label, epochs=5, callbacks=[tensorboard])优化算法相关
使用深层网络
随着神经网络的深度加深,模型能学习到更加复杂的问题,功能也更加强大。
超参数
典型的超参数有:
- 学习速率:α
- 迭代次数:N
- 隐藏层的层数:L
- 每一层的神经元个数:n[1],n[2],…
- 激活函数 g(z) 的选择
梯度消失
在梯度函数上出现的以指数级递增或者递减的情况分别称为梯度爆炸或者梯度消失。
假设g(z) = z, b^{[l]} = 0,对于目标输出有:\hat{y} = W^{[L]}W^{[L-1]}…W^{[2]}W^{[1]}X
- 对于$$W^{[l]}$$的值大于 1 的情况,激活函数的值将以指数级递增;
- 对于$$W^{[l]}$$的值小于 1 的情况,激活函数的值将以指数级递减。
根据不同情况梯度函数也会以指数级递增或递减,导致训练导数难度上升,梯度下降算法的步长会变得非常小,需要训练的时间将会非常长。
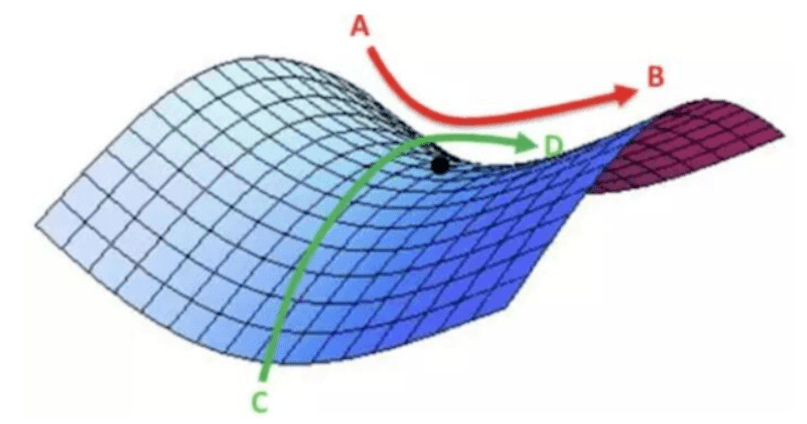
局部最优
鞍点(saddle)是函数上的导数为零,但不是轴上局部极值的点。通常梯度为零的点是上图所示的鞍点,而非局部最小值。减少损失的难度也来自误差曲面中的鞍点,而不是局部最低点。鞍点附近的平稳段会使得学习非常缓慢,而这也是需要后面的动量梯度下降法、RMSProp 以及 Adam 优化算法能够加速学习的原因,它们能帮助尽早走出平稳段。
批梯度下降算法Batch Gradient Descent
同时处理整个训练集,通过对所有的样本的计算来求解梯度的方向。
小批量梯度下降法Mini-Batch Gradient Descent
Mini-Batch 梯度下降法()每次同时处理固定大小的数据集。
mini-batch 的大小为 1,即是随机梯度下降法(stochastic gradient descent)
梯度下降优化影响
- batch 梯度下降法:
- 对所有 m 个训练样本执行一次梯度下降,每一次迭代时间较长,训练过程慢;
- 相对噪声低一些,成本函数总是向减小的方向下降。
- 随机梯度下降法(Mini-Batch=1):
- 对每一个训练样本执行一次梯度下降,训练速度快,但丢失了向量化带来的计算加速;
- 有很多噪声,需要适当减小学习率,成本函数总体趋势向全局最小值靠近,但永远不会收敛,而是一直在最小值附近波动。

指数加权平均
指数加权平均(Exponentially Weight Average)是一种常用的序列数据处理方式,通常用在序列场景如金融序列分析、温度变化序列分析。
通过指数加权的公式即:
S_t = \begin{cases} Y_1, &t = 1 \ \beta S_{t-1} + (1-\beta)Y_t, &t > 1 \end{cases}
其中Y_{t}为 t 下的实际值,S_{t}为t下加权平均后的值,\beta为权重值。
动量梯度下降法
动量梯度下降(Gradient Descent with Momentum)是计算梯度的指数加权平均数,并利用该值来更新参数值。动量梯度下降法的整个过程为:
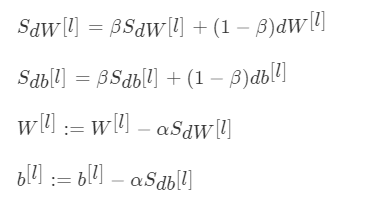
使用动量梯度下降时,通过累加过去的梯度值来减少抵达最小值路径上的波动,加速了收敛,因此在横轴方向下降得更快,从而得到图中红色或者紫色的曲线。当前后梯度方向一致时,动量梯度下降能够加速学习;而前后梯度方向不一致时,动量梯度下降能够抑制震荡。

RMSProp 算法
RMSProp(Root Mean Square Prop)算法是在对梯度进行指数加权平均的基础上,引入平方和平方根。
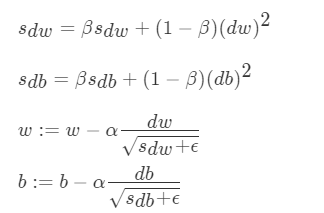
其中ϵ是一个非常小的数,防止分母太小导致不稳定。
最常用:Adam算法
Adam 优化算法(Adaptive Moment Estimation,自适应矩估计)将 Momentum 和 RMSProp 算法结合在一起。
tf.train.AdamOptimizer(learning_rate=0.001, beta1=0.9, beta2=0.999,epsilon=1e-08,name='Adam')注:β1、β2、ϵ 通常不需要调试
学习率衰减
如果设置一个固定的学习率 α
- 在最小值点附近,由于不同的 batch 中存在一定的噪声,因此不会精确收敛,而是始终
在最小值周围一个较大的范围内波动。 - 如果随着时间慢慢减少学习率 α 的大小,在初期 α 较大时,下降的步长较大,能以较快的速度进行梯度下降;而后期逐步减小 α 的值,即减小步长,有助于算法的收敛,更容易接近最优解。
最常用的学习率衰减方法:\alpha = \frac{1}{1 + decay_rate * epoch_num} * \alpha_0
其中,decay_rate为衰减率,epoch_num为将所有的训练样本完整过一遍的次数。
还有一种指数衰减
- $$\alpha = 0.95^{epoch_num} * \alpha_0$$

 从0开始学AI
从0开始学AI

 关于 LearnKu
关于 LearnKu



