1.动态数组

1.0

1.0

代码仓库【更新中】：github.com/jinrunheng/datastructur...

一：什么是数组

数组应该是我们在学习任何一种编程语言最早接触到的数据结构了。它是一种相同数据类型的元素存储的集合；数组中各个元素的存储是有先后顺序地，并且它们在内存中也会按照这样的顺序连续存放在一起。

二：Java 中数组的声明与遍历

Java 中数组的声明

在 Java 语言中，数组常规的声明方法有三种：

// 第一种
int[] students = new int[50];
// 第二种
int [] scores = new int [3]{99,88,79};
// 第三种
String [] hobby = {"拳击","健身","跑步"}

无论是哪一种声明方式，都可以看出数组的声明直接或间接地指定了数组的大小，只有在声明数组时，告诉计算机数组的大小，计算机才可以在指定的内存中为你声明的数组开辟一串连续的空间。

我们可以想象一连串小格子一个挨着一个紧密地拼凑在一起,每一个小格子都装着一个数据，而装着数据的小格子又对应计算机内存上的一个地址，每个小格子所对应的地址是连续的……

Java 中数组的遍历

除了我们熟知的 while 循环，for 循环等基本的遍历方式外，数组还支持 Java 8 引入的 foreach 遍历：

// 声明数组：
int [] scores = new int[50];
// 普通for循环
for(int i=0;i<scores.length;i++){
      System.out.println(score);
}
// foreach遍历
for(int score:scores){
      System.out.println(score);
}

因为数组在内存中是连续排布的，所以数组本身就具有可遍历的能力。

三：数组天生的优势——索引

数组最大的优势就是通过索引可以快速查询一个元素。因为数组在内存中开辟了一段空间，这一段连续的空间就是用来存储数组元素的，所以当我们想获取某一个数组索引的元素时，计算机只要通过这个索引就可以在开辟的内存空间中，找到存放这个元素的地址，继而通过内存地址就可以快速查询到这个元素。我们将索引查询的时间复杂度定义为O(1)。在后文有关于时间复杂度的介绍。

当数组的索引变得有一定的语意时，数组的应用就更加方便了。

例如：

int [] students = new int [50];如果索引代表的是班级里学生们的学号，如：students[21]代表的是学号为21号的学生，那么这种索引就变得非常有意义。但并非所有有语意的数组索引都适用，例如一个公司有10名员工，现在需要将员工信息存储于一个emp[]数组当中，如果将员工的身份证号作为索引去创建一个数组，那么显然是不合理的。虽然索引变得有意义，但是计算机为了存储10名员工的信息就要在内存上开辟身份证号长度的内存去存储，实在是大大浪费了空间。索引最好建立在有语意的前提下，但是一定要合理。

四：动态数组

什么是动态数组？

了解Java的人一定知道，Java Collecion里面，ArrayList的底层实现原理就是动态数组，那么动态数组的含义是什么呢？

在上文我们说过，如果想要声明定义一个数组，都需要直接或间接地告诉计算机我们要声明的数组的大小，只有计算机知道数组的大小后，才可以为我们的数组分配具体的内存空间。但是这样一来，数组就变得不是那么灵活了，当数组元素已满，我们就无法继续添加元素了。如果我们开辟了1000个元素空间的数组，但是仅仅存储10个元素，那这种情况也是不合理的，我们希望数组能够通过自己的存储元素的实际数量去调节自己的容量大小，这就需要数组具备动态的能力。Java 提供的数组不具备动态能力，所以，我们需要自己封装一个我们自己的数组，这个数组需要具备动态调节自身容量大小的能力，我们将这种数组定义为动态数组。

动态数组的原理

已知数组：

int[] data = new int[5];

数组目前元素已满

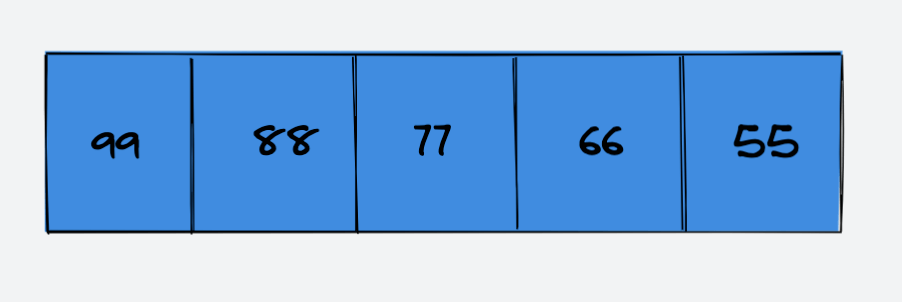
该数组已经无法再继续添加元素了，所以我们需要初始化一个新的数组，其容量为 data 的 2 倍，即：10

int[] newData = new int[10];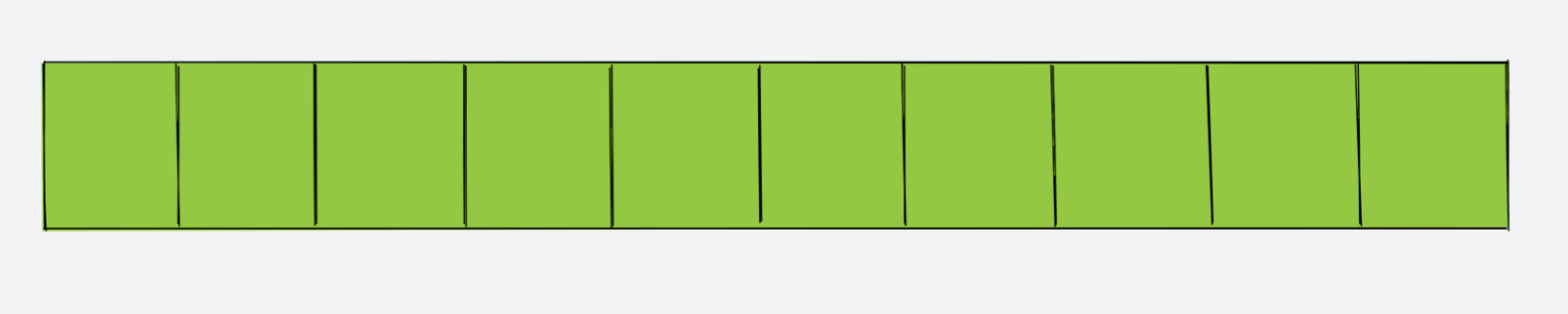

然后，将原数组的所有元素都赋值给新数组：

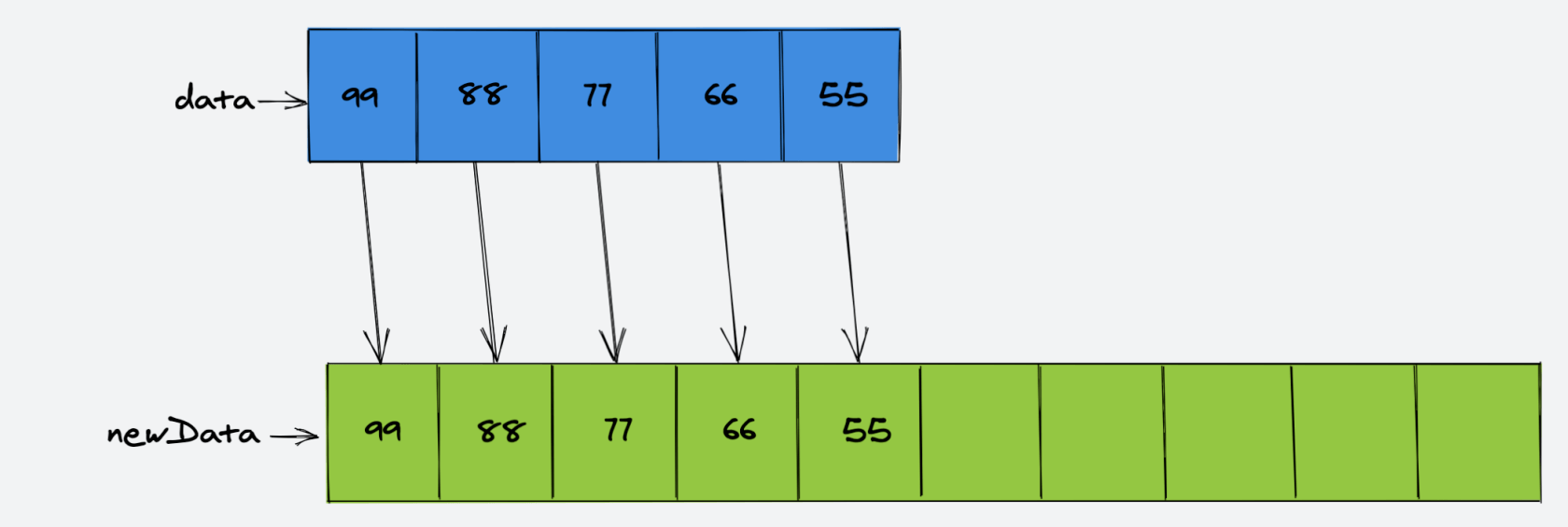
再将原数组的引用 data 指向新的数组：

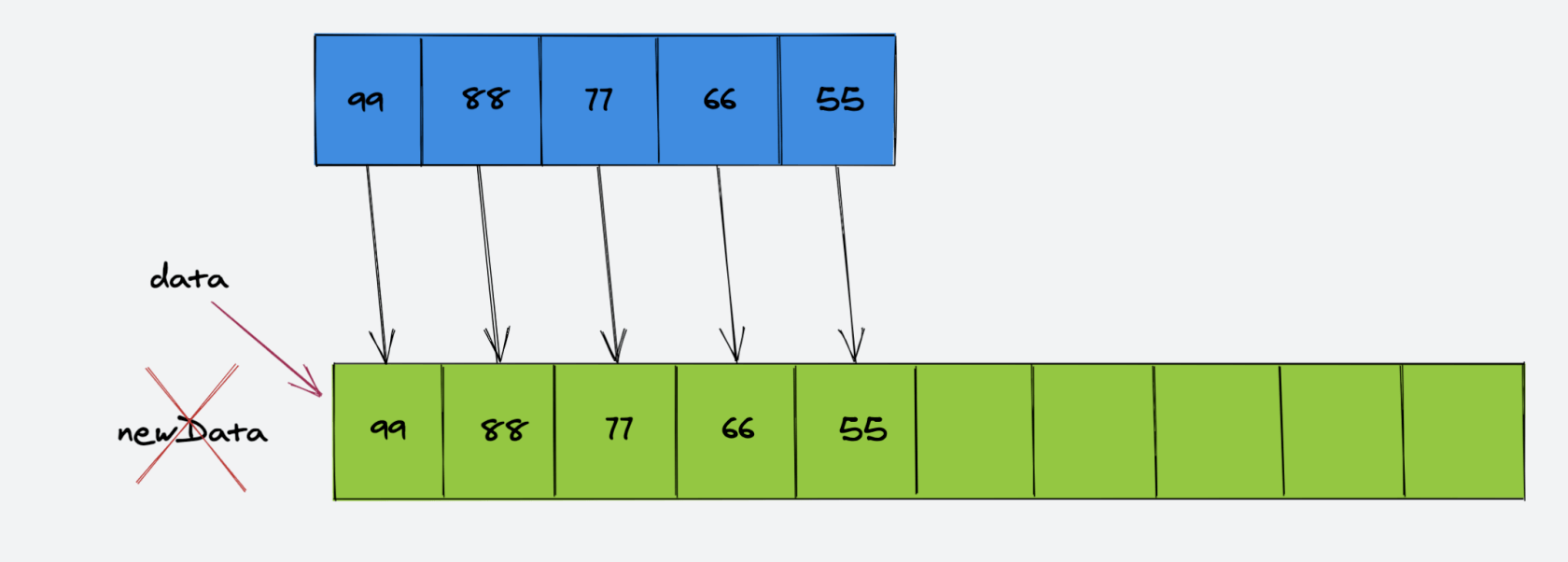
我们将这个过程转换为代码：

public void resize(int newCapacity){
    E[] newData = (E[])new Object[newCapacity];
    for(int i = 0; i < size; i++){
        newData[i] = data[i];
    }
    data = newData;
}

我们将动态数组扩容或缩容的过程封装成了一个方法：resize。在方法中，我们使用了泛型，用来表示所有类型的数组。

五：封装自己的数组类

代码地址

主要的方法有：添加元素，删除元素，修改元素，查询元素，resize

添加元素

方法签名：add(E e,int index)

该方法可以在指定的合法位置添加一个元素

示例：在索引 index = 1 处添加元素 88

原数组：

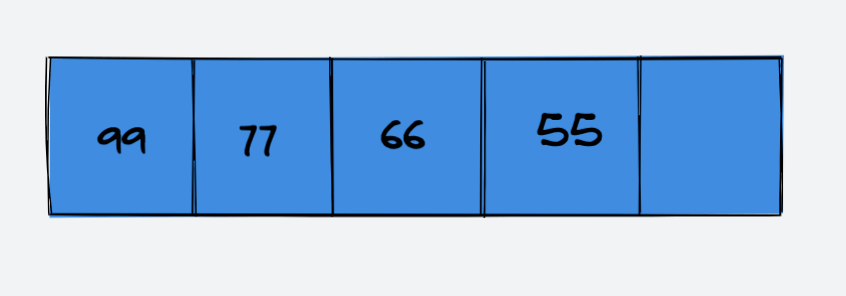
在索引 index = 1处添加元素 88

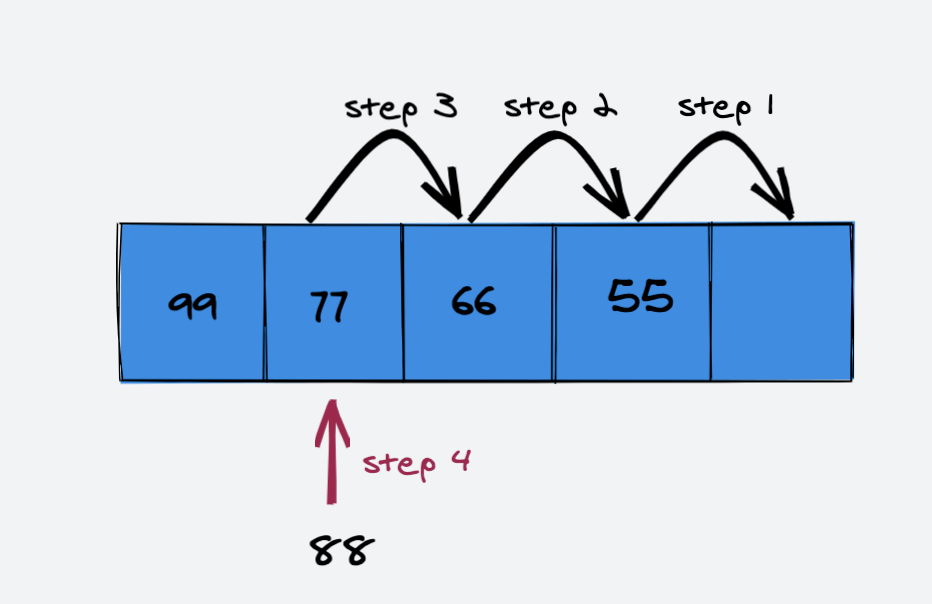
删除元素

方法签名：E remove(int index)

该方法可以删除指定的合法位置的元素

示例：删除索引 index = 1 处的元素 88

原数组：

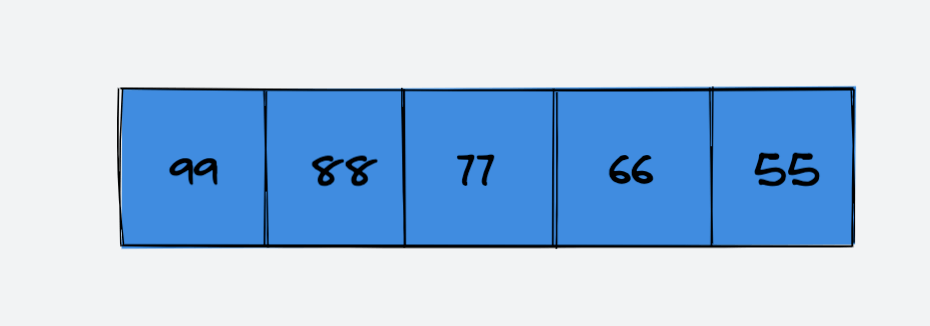
删除索引 index = 1 处的元素 88：

删除元素88后的数组：

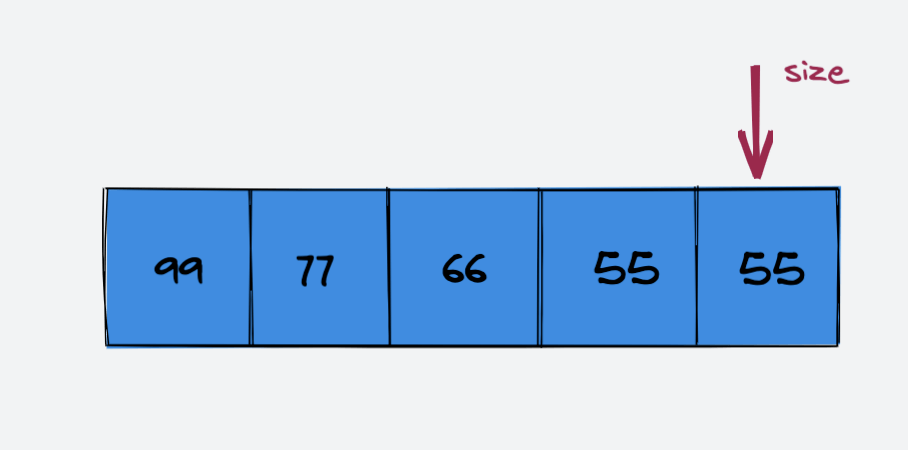
可以看到，删除元素88后，索引 index=4 处的元素依旧存在。

以用户的角度来看，用户是无法访问data[size] 这个元素的，并且，随着用户下一次添加元素，该位置的元素会被新添加的元素替换掉，所以即便我们不去处理它也无关紧要。

不过，这个位置仍然指向一个对象，并且该对象我们永远都访问不到，GC 也无法对其进行回收。这样的对象，被称为：”Loitering Objects”，它们虽然不会造成内存泄漏，不过却无法访问，理应被GC回收。所以，我们最好是手动对其进行回收（非必需）。

只需要让：

data[size] = null

即可。

修改元素与查询元素

修改元素与查询元素十分简单，这得益于数组的特性：索引。所以我们可以快速定位到索引的位置对其进行修改或查询返回，这里就不再赘述了。

六：复杂度分析

我们所接触到的最常见的时间复杂度有：O(1),O(n),O(n logn),O(n^2),等等。

其中 O() 描述的是算法的运行时间和输入数据的关系。拿数组的索引举例，数组的索引就是一个O(1) 级别的算法，因为知道索引获取元素的过程和数据的数量级没有关系，也就是说无论数组开辟了10的空间还是开辟了100万的内存空间，索引任一下标的时间都是一个常量。再例如程序：

public static int sum(int[]nums){
    int sum = 0;
    for(int num:nums){
          sum+=num;
    }
    return sum;
}

上面的这个对数组求和的算法就是一个O(n) 级别的算法。

程序是计算nums数组所有元素的和，计算出结果需要将nums数组从头至尾遍历一边，而遍历这个过程则与nums元素的数量n呈线性关系，随着元素个数n越来越大，遍历需要的时间就越来越长。当然，这个时间复杂度分析其实也忽略了很多常数及一些细节，包括使用的语言不同，程序消耗的时间也是有差异的，所以O()时间复杂度分析能够分析出的只是一种趋势。

O(1)，O(n)，O(n^2) 这三种级别的算法哪一种更优秀呢？

首先，O(1)级别的算法肯定是最优的，但是也有一定的弊端。拿数组的索引来说，数组之所以能够快速支持查找，就是因为它是一种以空间来换取时间的数据结构。如果数据的数量级是千万级的，那么数组就要在内存中开辟能够存储千万级数据的连续内存空间来支持数组的索引。

另外O(n)级别的算法一定要比O(n^2)级别的算法更优吗？其实也是不一定的，如T1 = 2000n+10000 这是一个O(n)级别的算法，T2 = n*n 这是一个O(n^2)级别的算法。当我们处理的业务逻辑中，n取值范围很小，例如在100以内时，很显然 T2的时间要小于T1,但是随着n的取值越来越大，O(n)算法的优势就会越来越大。

所以从 n 趋近于无穷大时，O(1)算法最优，O(n)算法要优于O(n^2)级别的算法。实际上也确实如此，在海量级的数据下，时间复杂度的优化对性能的提升是巨大的。

分析我们的动态数组中主要方法的时间复杂度

resize

• resize(): O(n)

添加元素

• addLast(e): O(1)

• addFirst(e): O(n)

• add(e,index): O(n)

删除元素

• removeLast(e): O(1)

• removeFirst(e): O(n)

• remove(e,index): O(n)

修改元素

• set(e,index): O(1)

查询元素

• get(index): O(1)

• contains(e): O(n)

• find(e): O(n)

七：均摊复杂度与防止复杂度震荡

在上面，我们简单分析了动态数组的增删改查操作的时间复杂度，但是除了“改”和“查”两种操作不涉及到resize外，添加元素和删除元素都有 resize 扩容与缩容这种机制在里面。

均摊复杂度

以时间复杂度为O(1)的方法addLast(E e)来举例。

如果初始化数组的原始capacity为10，开始时，数组内没有任何元素。一直使用addLast(E e)向数组末尾添加元素，在添加10次后，即第十一次再次添加元素则触发了一次扩容操作，扩容后的capacity为20，即原来的capacity的2倍。而在第21次添加元素操作时，又再次触发了扩容的操作。

这个过程我们可以通过示例图来进行理解：

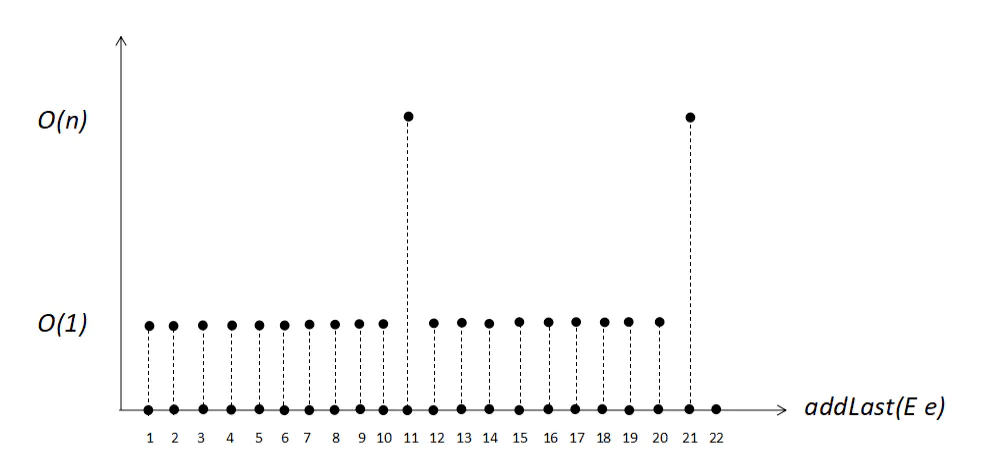
第一次 addLast 操作，时间复杂度为 O(1)

第二次 addLast 操作，时间复杂度为 O(1)

第三次 addLast 操作，时间复杂度为 O(1)

… …

第 n + 1(data.length + 1) 次 addLast 操作，触发 resize，时间复杂度为 O(n)

也就是说：第n+1次addLast操作会触发一次resize方法。

如果将O(1)的操作称作1次基本操作的话，从第1次添加元素至第n+1次添加操作共进行了2n + 1次基本操作（resize相当于n次基本操作，并且共执行了n+1次addLast操作，所以算上 resize 共执行了 2n + 1 次基本操作）。

计算机做了2n+1次基本操作——即：O(1) 的操作，那么平均下来，每1次addLast，计算机就要做(2n + 1)/(n+1)次O(1)操作。也就是说当n这个数字趋近无穷大时，则每1次addLast操作，计算机会进行2次基本的O(1)操作，那么，这就就可以说明——addLast操作和n没有关系，它仍然是一个O(1)级别的算法。

以上分析就是均摊复杂度的分析思想，同理：其他的方法也可以用均摊复杂度来进行分析，得到的结果是一致的，resize虽然会触发O(n)的操作，但是将resize的O(n)操作平均到每一次O(1)操作上，对我们之前分析的时间复杂度并无结果上的变化。

防止复杂度震荡

对于 remove 方法，我们设置了缩容的机制：当数组的 size 为 capacity 的四分之一时，触发缩容机制，将 capacity 缩小为原来的一半。

/**
 * @param index 删除 index 位置的元素
 * @return 返回删除的元素值
 */
public E remove(int index) {
    if (size <= 0) {
        throw new IllegalArgumentException("Remove failed. Array is empty!");
    }
    if (index < 0 || index >= size) {
        throw new IllegalArgumentException("Delete failed. Index is illegal!");
    }
    E ret = data[index];
    for (int i = index; i < size - 1; i++) {
        data[i] = data[i + 1];
    }
    size--;
    data[size] = null; // loitering objects

    // 缩容
    if (size == data.length / 4 && data.length / 2 != 0) {
        resize(data.length / 2);
    }

    return ret;
}

为什么，我们不将缩容机制设置为：当数组的 size 为 capacity 的二分之一时，触发所容机制，将 capacity 缩小为原来的一半呢？

如果我们将缩容机制改为：

// 缩容
if (size == data.length / 2 && data.length / 2 != 0) {
    resize(data.length / 2);
}

那么就会出现复杂度震荡问题

假设，数组内元素的情况如下：

当前数组的 size 为 5，capacity 为 5，现在对数组进行如下操作：

1. addLast —–> 触发扩容

2. removeLast —–> 触发缩容

3. addLast —–> 触发扩容

4. removeLast —–> 触发缩容

5. … …

我们已经看到问题的所在，原本为 O(1) 时间复杂度的addLast和removeLast 因为不断触发扩容与缩容操作，反而退化成O(n)的算法。

出现这个问题的原因在于我们的remove方法中，resize 操作过于着急（eager），造成了复杂度震荡。解决方法为 Lazy 策略。

当数组元素的个数到capacity的一半时，不着急去缩容，而是等到size==capacity/4时，再将capacity的容积缩容为capacity/2。这样就可以避免复杂度震荡问题。