golang工程师应该会的数据结构与算法二叉树基本概念及其重要特性
@author 汪春波
二叉树的概念
二叉树是一个有限的结点集合，该集合或者为空，或者由一个根结点及其两棵互不相交的左、右二叉子树所组成。
二叉树的结点中有两棵子二叉树，分别称为左子树和右子树。因为二叉树可以为空，所以二叉树中的结点可能没有子结点，也可能只有一个左子结点（右子结点），也可能同时有左右两个子结点。如图4-9所示是二叉树的4种可能形态（如果把空树计算在内，则共有5种形态）。
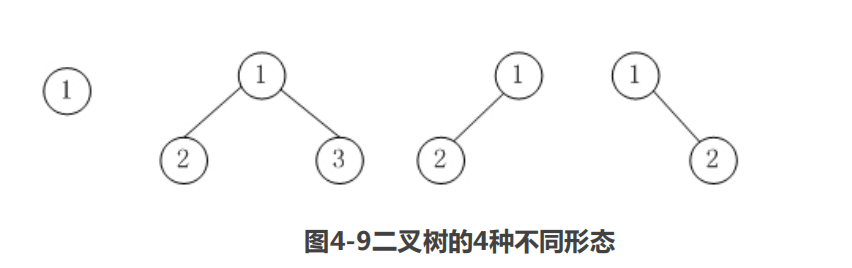
满二叉树与完全二叉树与非完全二叉树
在二叉树中，有两种表现极为特殊，即满二叉树和完全二叉树，如图4-10所示。
满二叉树：所有的度（就是节点）都是2，就称为满二叉树。
完全二叉树：从左向右边，的节点没有间断，即为完全二叉树。（有右节点，肯定有左节点，有右节点，不一定有左节点）
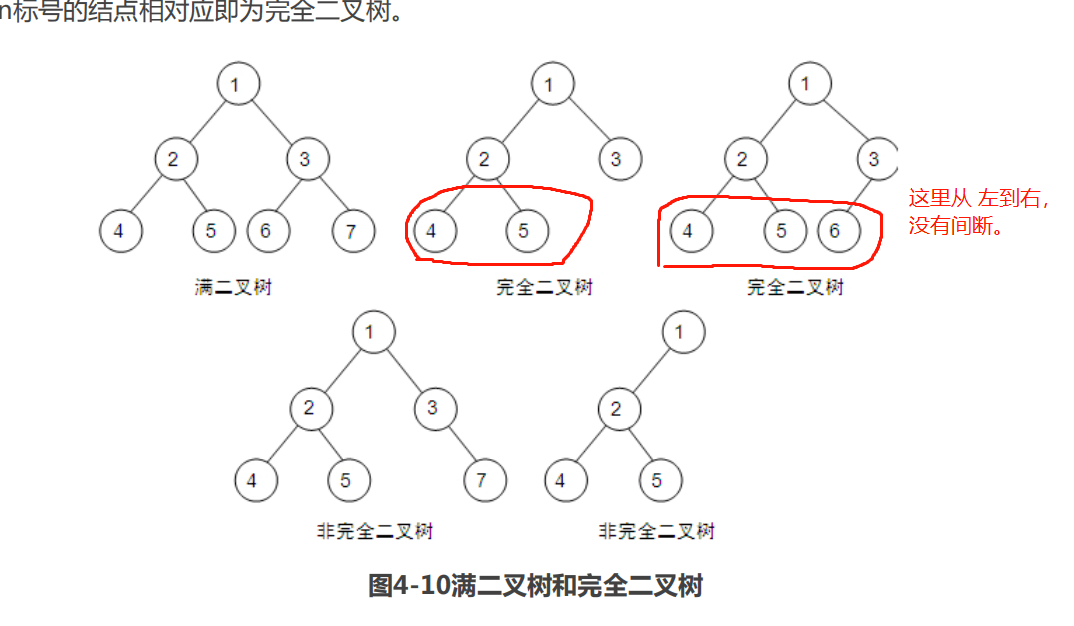
非完全二叉树：有间断了，就是非完全二叉树。依然如下图。
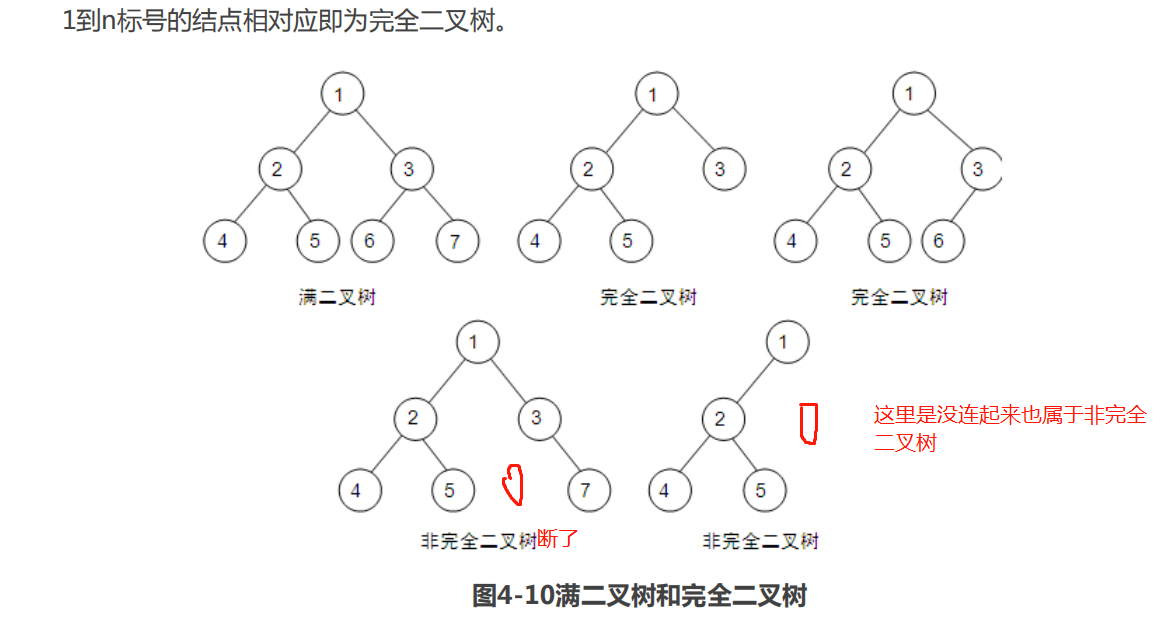
二叉树的重要特性
1. 在二叉树的第i层，最多有 2(i-1) 个节点(i>=1)。
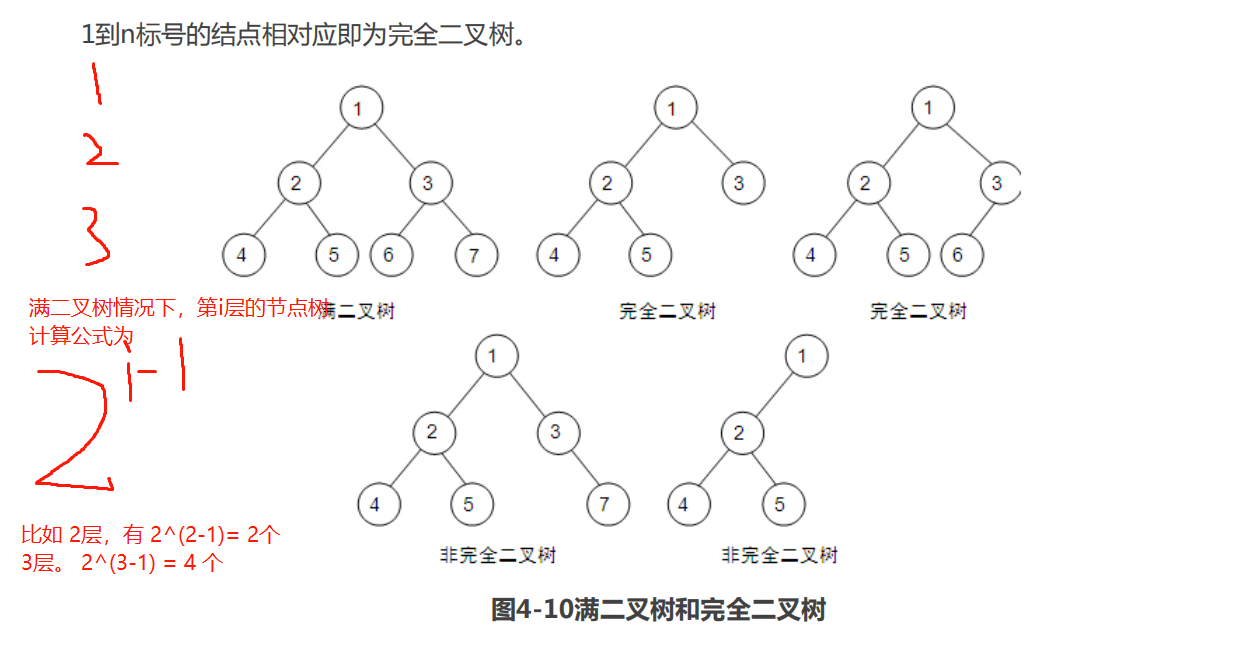
满二叉树就是最对的情况。
2. 深度（层次）为k的二叉树，最多有2^(k-1)个节点。
满树就是最多节点。
比如三层的，23 = 8 然而三层满树7个，所以公式推出，2(k-1)
3. 对任何一颗二叉树，如果其叶子节点数为n0，度为2的节点数为n2,为n0 = n2 + 1
![二叉树基本概念]
4. 如果对一棵有n个结点的完全二叉树的结点按层序编号（从第1层到 log2n+1层，每层从左 到右），则对任一结点i（1≤i≤n），有：
如果i=1，则结点i无父结点，是二叉树的根；如果i>1，则父结点是 \lfloor i/2 \rfloor ； [向下取整]
如果2i>n，则结点i为叶子结点，无左子结点；否则，其左子结点是结点2i；
如果2i+1>n，则结点i无右子结点，否则，其右子结点是结点2i+1。
在考试时，对这几个特性的灵活应用是十分关键的，因此应熟练的掌握它们，其实这些性质都 十分明显，只需绘制出二叉树，结合着体会将能更有效地记忆。
关于 LearnKu
粤公网安备 44030502004330号