golang工程师应该会的数据结构与算法图的存储结构
2. 图的存储结构
图有两种主要的存储结构，它们是邻接矩阵表示法和邻接表表示法，如表所示。
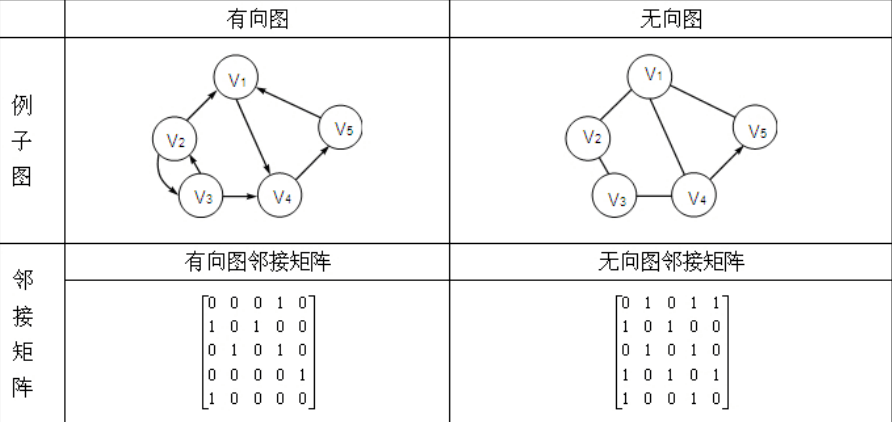
2.1 邻接矩阵
用一个n 阶 方阵R来存放图中各结点的关联信息，其矩阵元素R_i,_j定义为
R_i,_j=\left\{ \begin{aligned} 1 若顶点i到顶点j有邻接边 \\ 2 若顶点i到顶点j无邻接边 \\ \end{aligned} \right.
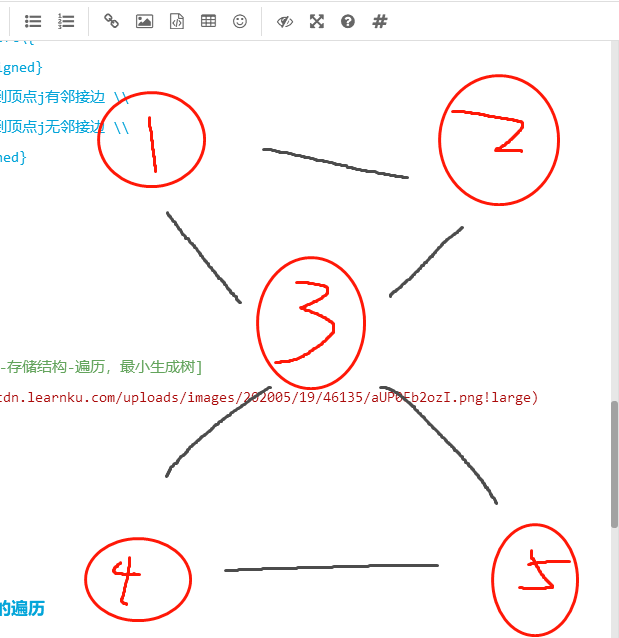
图里面有多少个结点
一般我们用一个n 阶 方阵R来存放图中各结点的关联信息。（方阵指长和列相等）
注意：图里面有多少个结点，就要用多少✖多少的矩阵。
如图，图中有5个结点，则生 5*5 方阵。
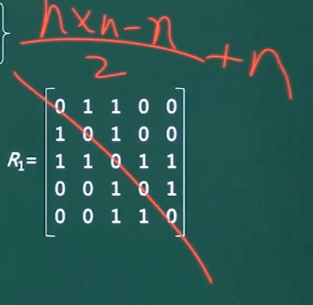
那么如下我们给出一个 R_1 矩阵（别问我是怎么生成的，就是画的。现在还没学到转化）
R_1=\left\{ \begin{aligned} 01100\\ 10100\\ 11011\\ 00101\\ 00110\\ \end{aligned} \right.
他们要存的话，完全图也是一个邻接矩阵，只要存一半即可。不管你是上三角，还是下三角，都可以。
我们计算的元素半身半三角公式为：（n*n-n)/2 +n
对上文矩阵中 0 和 1 的解析
如图，1 代表有邻接边（比如1到2）
0代表没有邻接边（比如 1到 4）
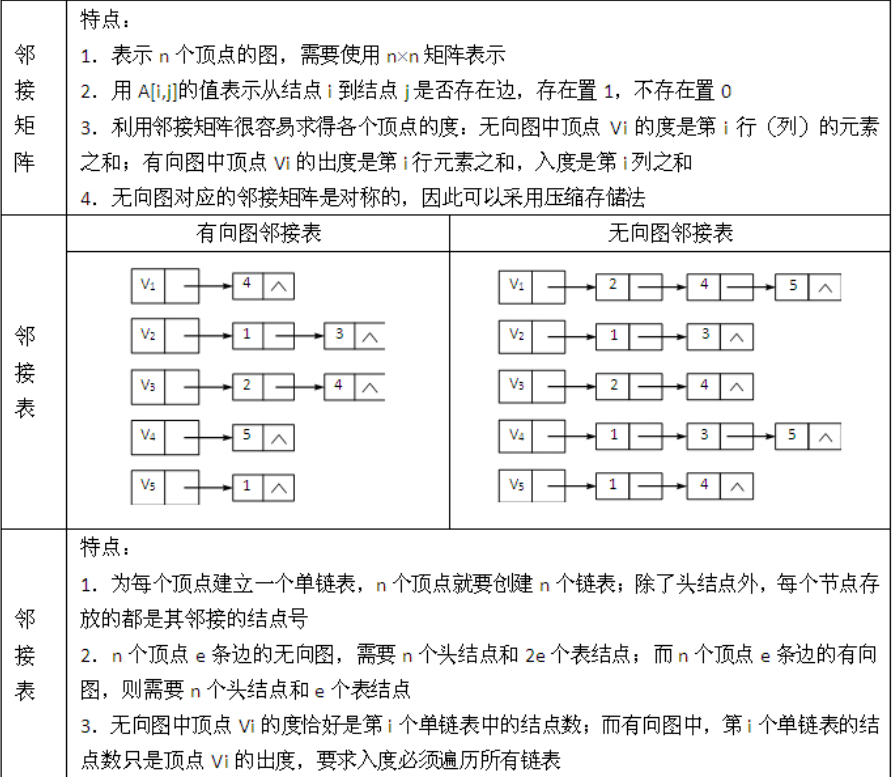
2.2 邻接表
首先把每个顶点的邻接顶点用列表示出来，然后用一个一维数组来顺序存储上面每个链表的头指针。
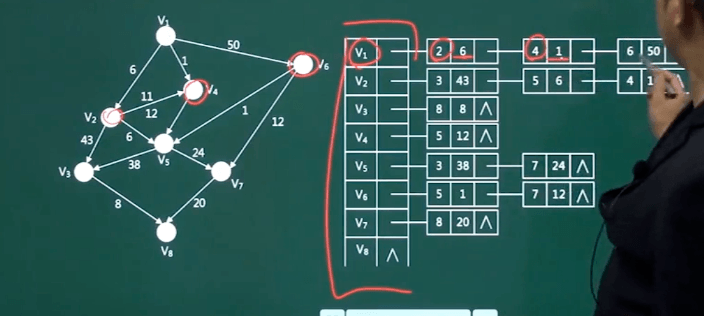
看图片我们来解释一下，左上角这个顶点V1,
可以到V2,V4,V6.
所以他有三个链。
一个是长度为六的V2，
一个是长度为一的V4。
还有一个长度为50的V6。
其他的依次类推。
依次如此排列，这就是邻接。
这个顶点的表头，可以到其他的链表，这就是邻接表。
PS
虽然你看文章只需要3分钟，但是我写它用了2小时。
一边学习，一边写文档不易。给点小点赞，支持一下吧。加油！
防爬虫说明
禁止 学习某地爬虫，知乎爬虫，CSDN 爬虫。
本文，首发在 learnku 社区。
@author
汪春波（www.shxdledu.cn）
关于 LearnKu
粤公网安备 44030502004330号