图的概念
图
图是一种比树更复杂的非线性结构,它是由顶点集合V和边集合E组成的,通常记做GG(V,E)。
它可以用来模拟现实世界中许多图状结构的事物与问题。
1. 图的相关概念
完全图
- 在无向图中,若每对顶点之间都有一条边相连,则称该图为完全图。

- 在有向图中,若每对顶点之间都有二条有向边相互练级,则称该图为完全图。
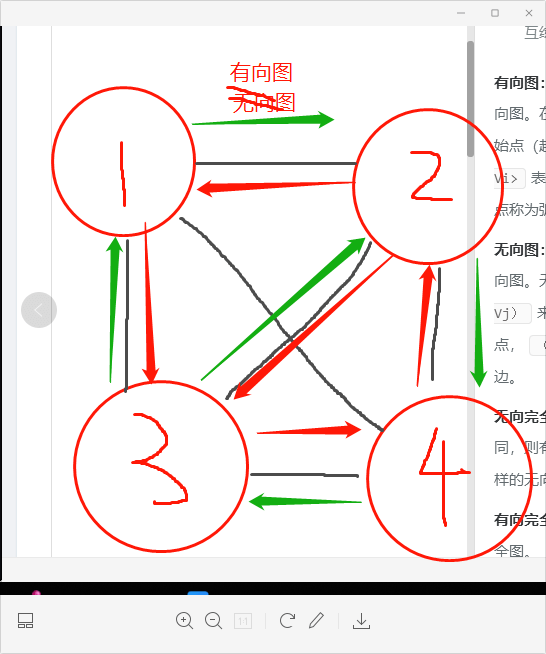
下面文字知道下即可:
有向图:若一个图中的每条边都是有方向的,则称为有向图。在有向图中,<Vi,Vj>表示一条有向边,Vi是始点(起点),Vj是终点。<Vi,Vj>和<Vj,Vi>表示的是两条不同的边。有向边也称为弧,边的始点称为弧头,终点称为弧尾。
无向图:若一个图中的每条边都是无方向的,则称为无向图。无向图的边是顶点的无序对,通常使用(Vi,Vj)来表示一条边,无向图的边没有起点和终点,(Vi,Vj)和(Vj,Vi)表示的是同一条边。
无向完全图:如果限定任何一条边的两个顶点都不相同,则有n个顶点的无向图至多有n(n-1)/2条边,这样的无向图称为无向完全图。
有向完全图:恰好有n(n-1)条边的有向图称为有向完全图。
连通图:如果图中两个顶点间存在路径,则称它们是连通的;而如果图中任意两个顶点间都是连通的,则称该图为连通图。

 golang工程师应该会的数据结构与算法
golang工程师应该会的数据结构与算法

 关于 LearnKu
关于 LearnKu



