Machine Learning（15） - K Means Clustering

引言

Machine Learning Algorithm 可以分为三类：Supervised Learning, Unsupervised Learning 和 Reinforcement Learning。

前面我们所学的都是 Supervised Learning，就是数据集里既有 Feature(特征）也有与之对应的 Label(即 target)。

与之相对的是 Unsupervised Learning，即只有 Feature(特征），没有 Label。我们需要从已知的 Features 中发现其内部的结构，然后将数据进行分类。

这节课要介绍的就是用于 Unsupervised Learning 的，非常流行的 K Means Algorithm。

假如给你这样一个数据集，要求将这些数据进行合理的分类，我们要怎么做呢？

首先，从视觉上，我们可能会大致将它分为如下两个集合。

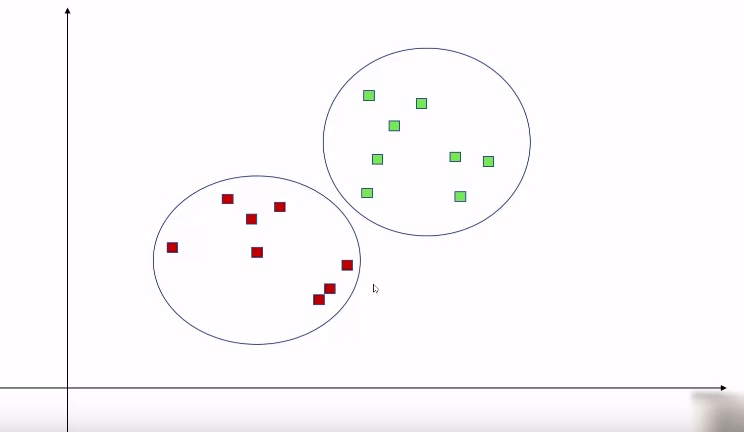
原理讲解

下面我们一步一步来看下 K Means Algorithm 的工作原理。

首先说明， K Means 中的 K 其实是一个参数，表示要将数据分为几个集合。K 被称作 centroid（字面结合实际理解，大概就是中心的意思）。

步骤一：这里按照我们上面的假设，可以把这些数据分为两个集合，也就是 K = 2, 即先随机选两个中心点（下图中的五角星）：

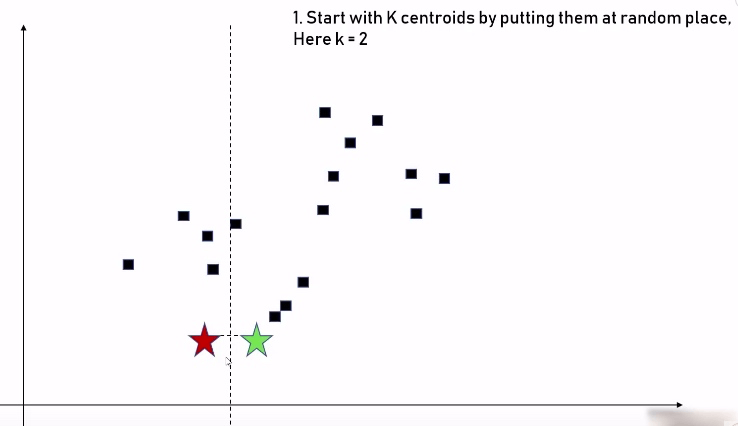
步骤二：分别比较每个数据点到这两个中心点的距离，距离哪个中心点最近，就被分到哪个中心点的集合：

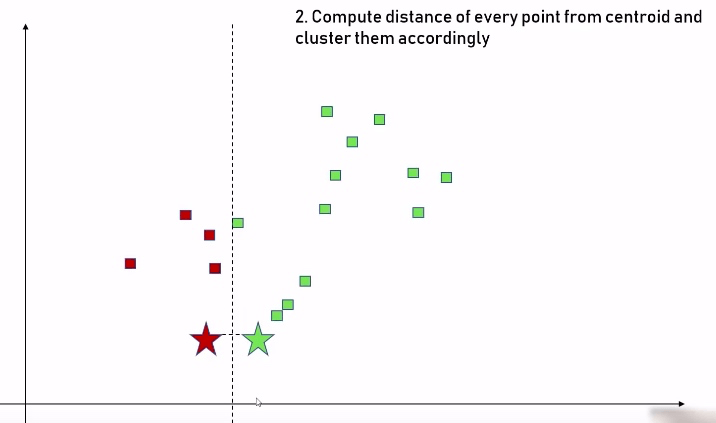
步骤三：我们将这两个中心点分别移到两个数据集的中心位置：

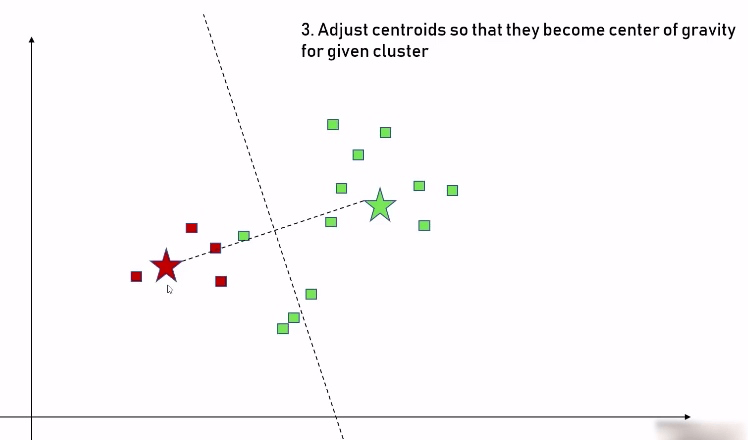
步骤四：重复步骤二，再次比较每个点到中心点的距离，重新调整每个集合里的数据：

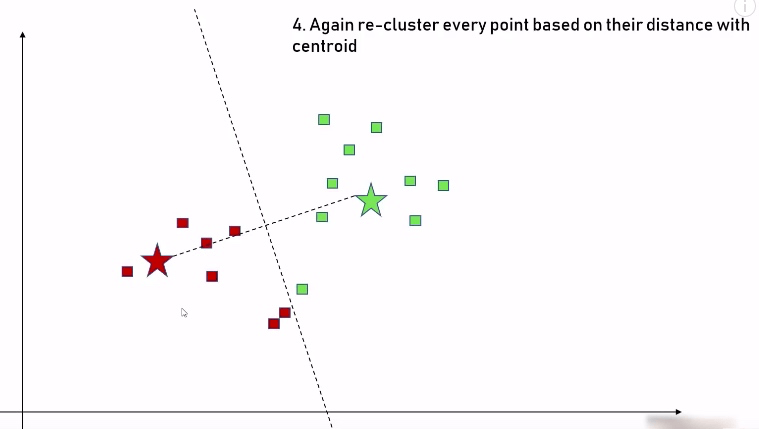
步骤五：根据上面的调整，我们又得到了新的数据集，此时重复步骤三，把中心点再次放到新的数据集的正中心的位置：

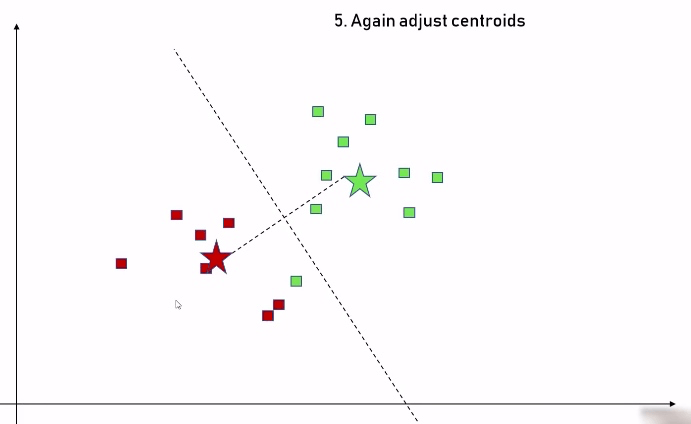
如此往复，直到不需要再做任何调整，表示我们已经将数据集做了最合理的分类：

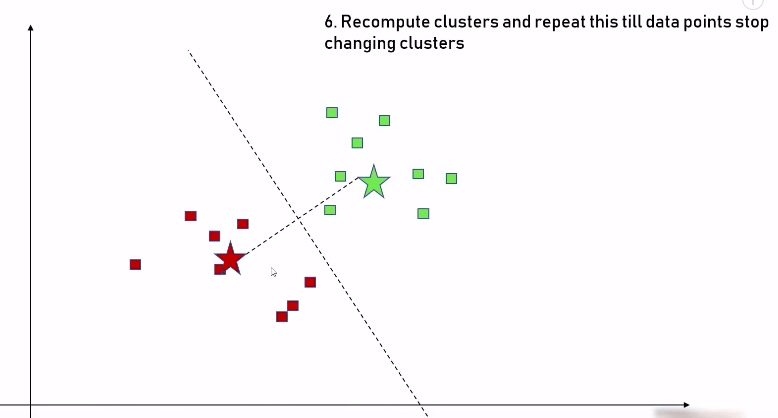
这是我们最终得到的数据分类：

以上就是对 Unsupervised Learning 的 K Means Algorithm 整个工作原理的介绍。

这个例子中的数据集非常简单，只有两个维度，但是在实际应用中，我们要分析的数据可能会有很多个维度。而且，假设 K = 2 是所有分析的前提条件。那难道 K 不能等于 3，4，5，6 吗？所以 K 究竟等于几才是最合理的呢？

寻找最佳 K 值

这里需要用到 SSE(Sum of Squared Errors)，也就是每个数据点到中心点的距离的平方的和。然后，根据 K 等于几，就有几个 SSE, 再将其加和。

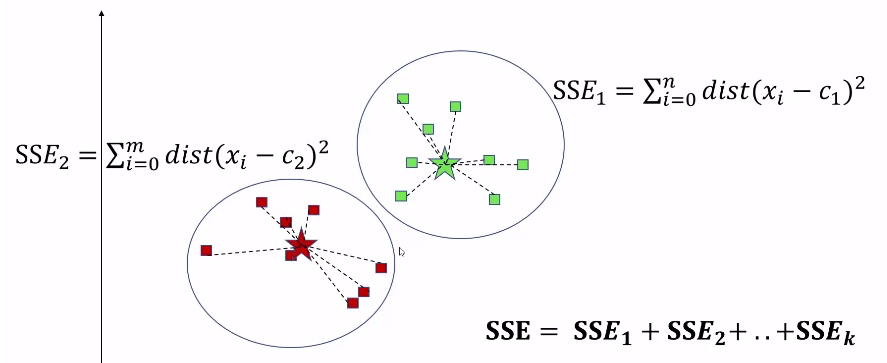
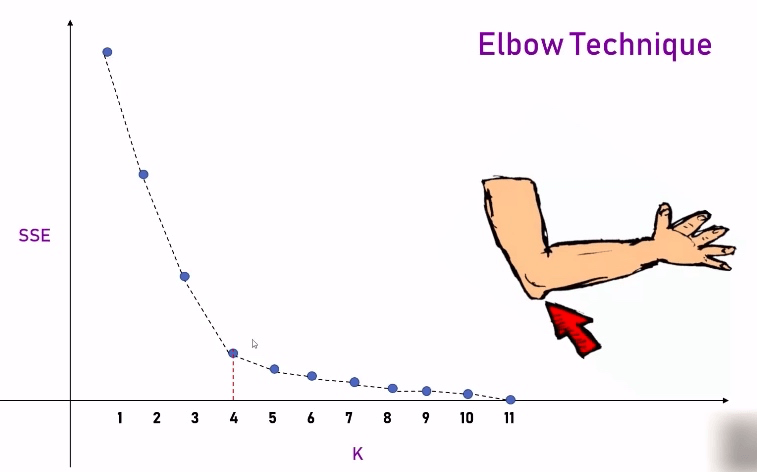
这样，我们把 K 的值从 1 取到 11，可以画出如下的曲线，根据 Elbow Technique, 在胳膊肘位置的那个拐点，就是最合理的 K 值。

理论结合实际

下面通过这样一个比较实际的例子来学习一下具体操作方法。

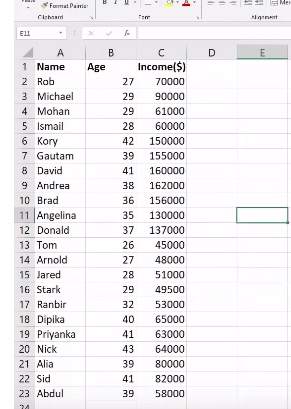
引入需要的包及数据

import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import MinMaxScaler
%matplotlib inline

df = pd.read_csv('/Users/rachel/Sites/pandas/py/ML/13_kmeans/income.csv')
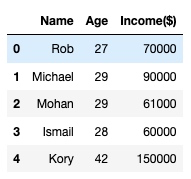
df.head()

输出：

以 scatter 的形式输出数据集

plt.scatter(df['Age'], df['Income($)'])

输出：

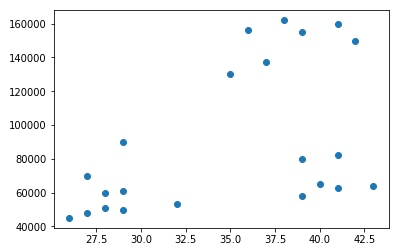
根据上图，以肉眼可见的能见度，我们暂且把数据集分成三份，即 K = 3.

创建 KMeans 对象

km = KMeans(n_clusters=3)
km

// 以下输出中的参数，都是可以用来调节对象的
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
    n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
    random_state=None, tol=0.0001, verbose=0)

模型的训练及预测

// 让 km 根据提供的数据集预测分类
y_predicted = km.fit_predict(df[['Age', 'Income($)']])
y_predicted

// 输出
array([0, 0, 2, 2, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 0, 0, 2],
      dtype=int32)

// 把预测的分类合并到数据集中      
df['cluster'] = y_predicted
df.head()

输出：

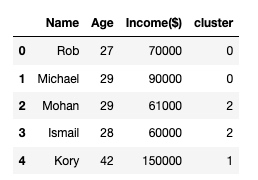
以 scatter 的形式输出数据集的分类，更直观地检测分类是否正确：

df1 = df[df.cluster == 0]
df2 = df[df.cluster == 1]
df3 = df[df.cluster == 2]

plt.scatter(df1.Age, df1['Income($)'], color='green')
plt.scatter(df2.Age, df2['Income($)'], color='red')
plt.scatter(df3.Age, df3['Income($)'], color='black')

plt.xlabel('Age')
plt.ylabel('Income($)')
plt.legend()

输出：

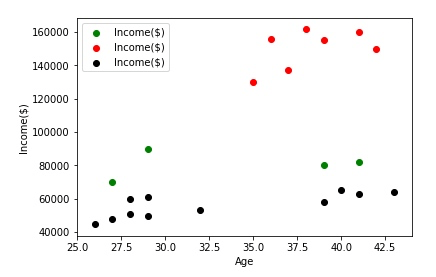
我们发现目前的分类是不正确的（绿色和黑色部分），这是由于 x 轴和 y 轴的数据范围差距太大导致的。

用 MinMaxScaler 解决数据范围导致的问题

scaler = MinMaxScaler()
scaler.fit(df[['Age']])
df.Age = scaler.transform(df[['Age']])

scaler.fit(df[['Income($)']])
df['Income($)'] = scaler.transform(df[['Income($)']])
df.head()

输出：

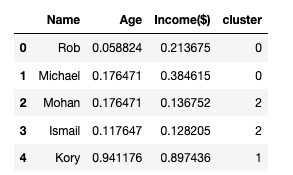
现在数据的 x 和 y 轴的值都是 0-1。

现在用这个数据集重新训练模型(重复上面的操作）:

km = KMeans(n_clusters=3)
km

// 输出
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
    n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
    random_state=None, tol=0.0001, verbose=0)

y_predicted = km.fit_predict(df[['Age', 'Income($)']])
y_predicted

// 输出
array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 2],
      dtype=int32)

df['cluster'] = y_predicted

// 输出每个集合中心点的坐标
centers = km.cluster_centers_
centers
// 输出
array([[0.1372549 , 0.11633428],
       [0.72268908, 0.8974359 ],
       [0.85294118, 0.2022792 ]])

df1 = df[df.cluster == 0]
df2 = df[df.cluster == 1]
df3 = df[df.cluster == 2]

plt.scatter(df1.Age, df1['Income($)'], color='green')
plt.scatter(df2.Age, df2['Income($)'], color='red')
plt.scatter(df3.Age, df3['Income($)'], color='black')
plt.scatter(centers[:,0], centers[:,1], color='purple', marker='*')

plt.xlabel('Age')
plt.ylabel('Income($)')
plt.legend()

输出：

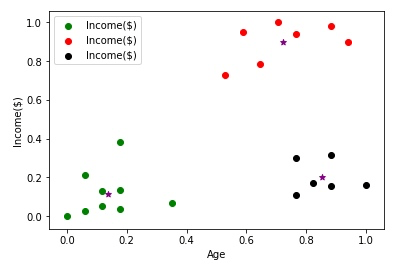
现在可以看到数据集被正确地分类了。

求出 K 的 值

现在又回到我们开始提出的问题，目前的分析都是基于我们假设 K = 3 来进行的， 那么，如果遇到复杂的数据，K 的值怎么求?

这里就来说一下 Elbow Technique 的用法:

k_rng = range(1, 10)
sse = []
for k in k_rng:
    km = KMeans(n_clusters=k)
    km.fit_predict(df[['Age', 'Income($)']])
    sse.append(km.inertia_)

sse
// 输出
[5.434011511988176,
 2.0911363886990766,
 0.47507834985530945,
 0.3491047094419564,
 0.2664030124668415,
 0.22443334487241418,
 0.18269415744795037,
 0.14072448985352304,
 0.10188787724979424]

plt.xlabel('K')
plt.ylabel('SSE')
plt.plot(k_rng, sse)

输出：

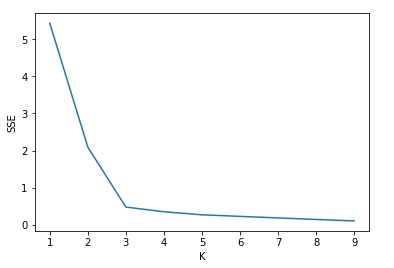
所以这里证明了我们假设 K = 3 是正确的。

本作品采用《CC 协议》，转载必须注明作者和本文链接