带权图的表示

一、介绍

带权图(Weighted Graph)：带权图就是指图中的每一条边都有对应的一个或一组值，通常情况下这个值的是数值。
如：在交通运输网中，边上的权值可能表示的是路程，也可能表示
的是运输费用（显然二者都是数字）。不过，边上的权值也有可能
是其它东西，比如说是一个字符串，甚至是一个更加复杂的数据包，
里面集合了更多的数据。

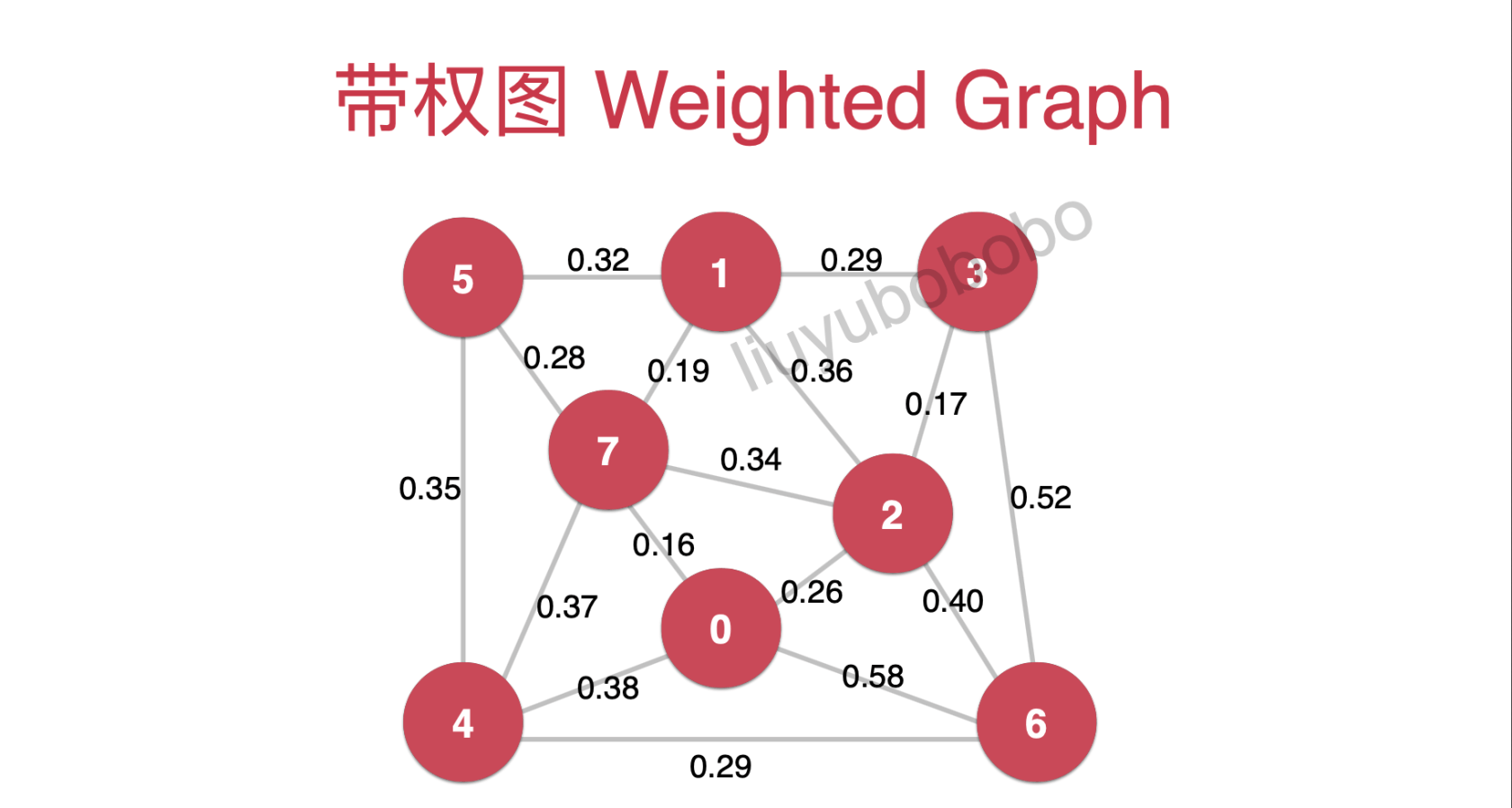
二、表示方法

1. 邻接表
   在无权图中邻接表只存放了相应顶点，而现在带权图既需要存放顶点又需要存放权值，所以在带权图中的需要一个Edge的类来表示有权图的顶点和权值，表示方法如下：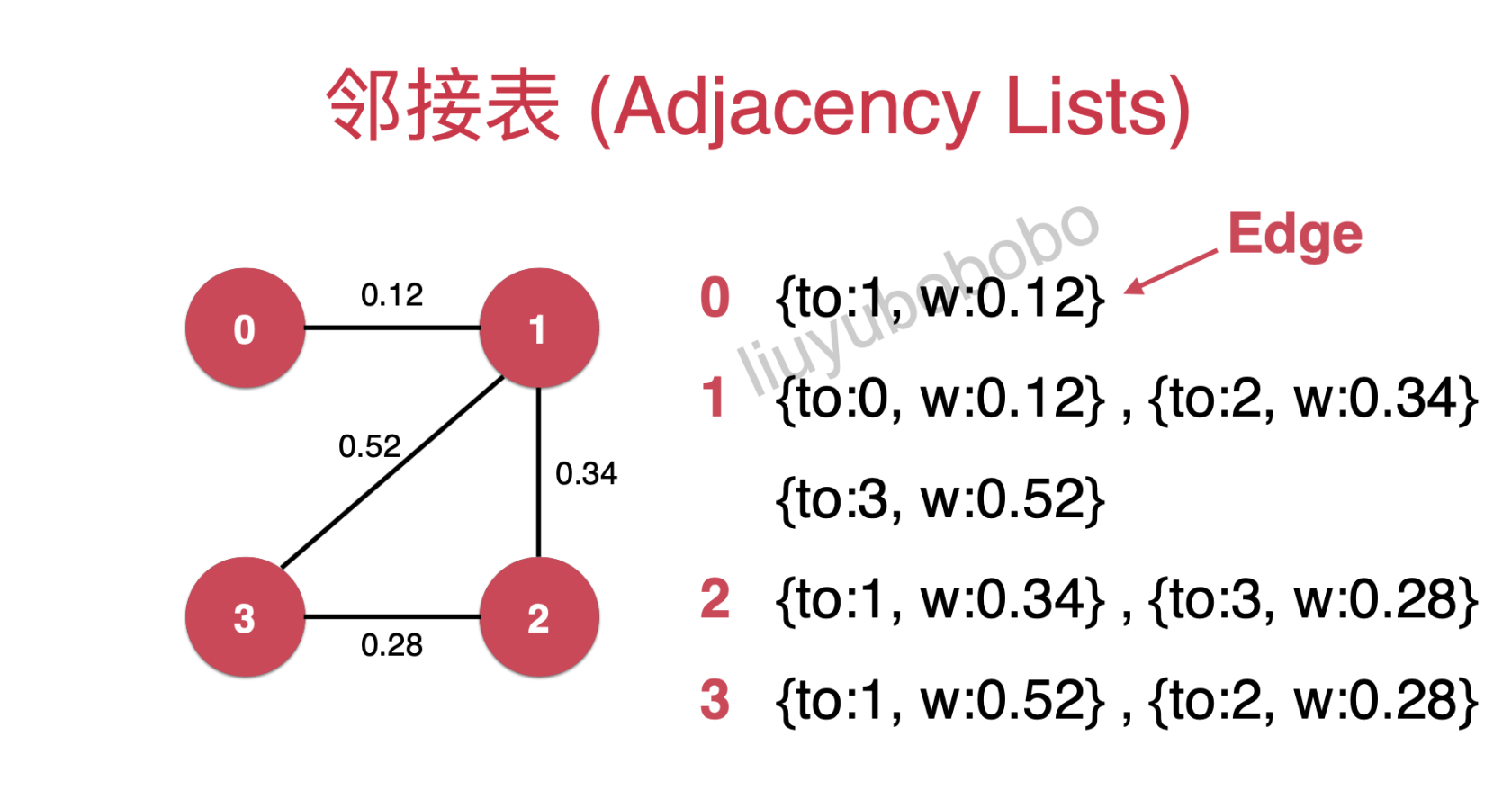
   
   这里再将权值的类型写成指针类型

2. 邻接矩阵
   在带权中不再使用bool值，但是这里为了统一接口，统一将邻接矩阵的表示写成一个Edge类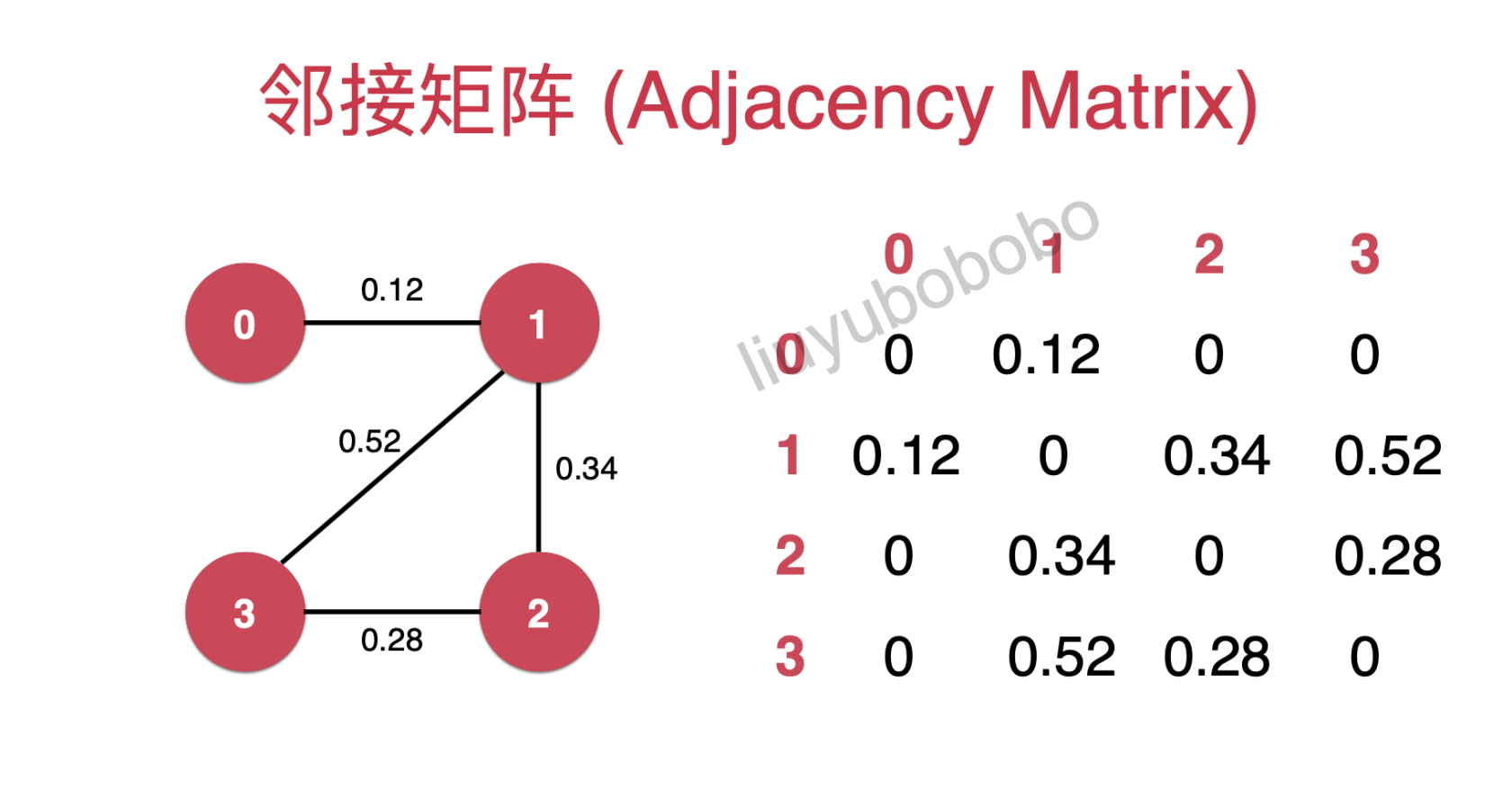
   
   这里再将权值的类型写成指针类型

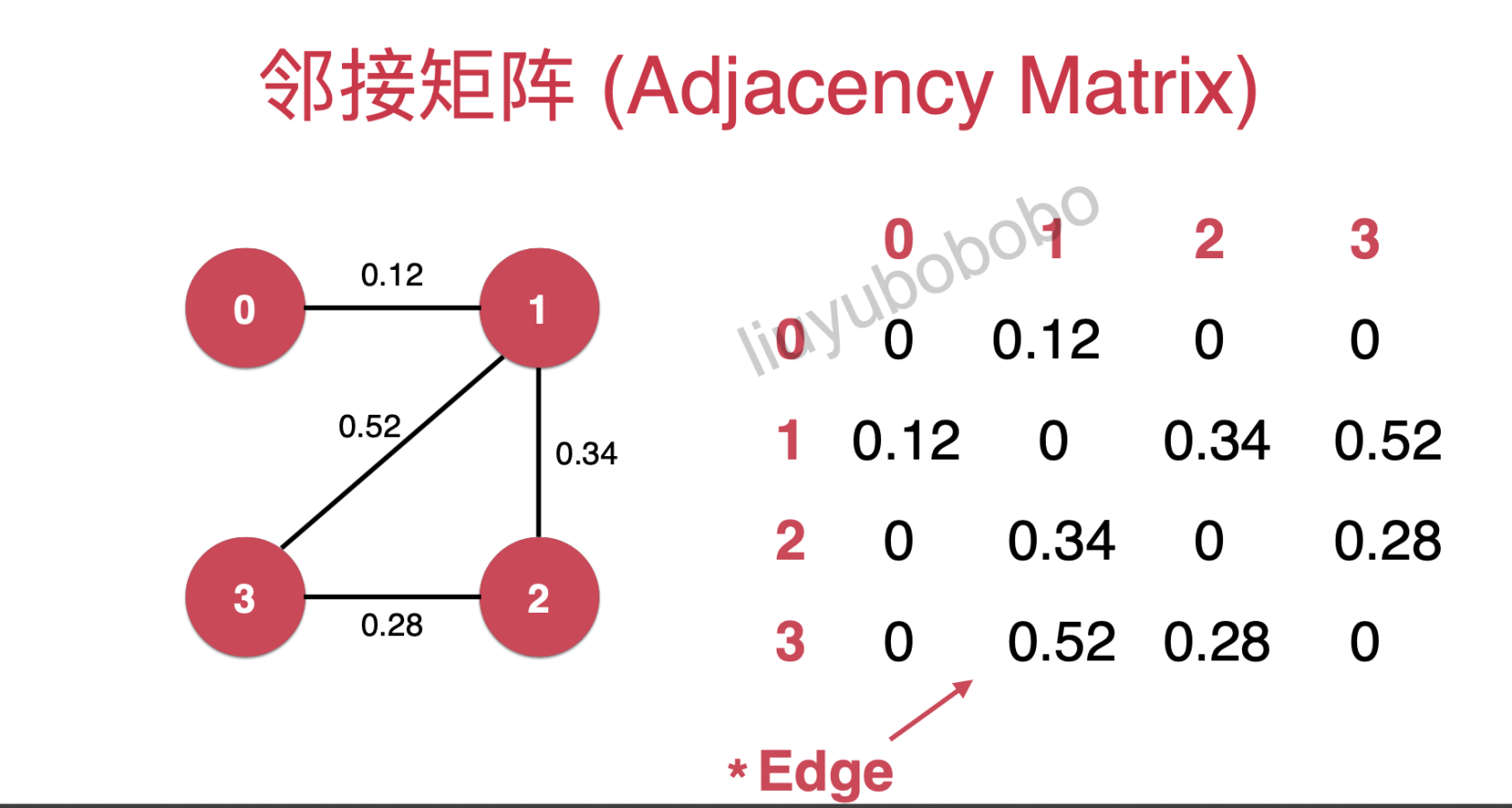
三、带权图的实现

1. 首先需要编写一个Edge的类，用来表示带全图

   #include <iostream>
   #include <cassert>
   using namespace std;
   // 边
   //使用模板类型Weight
   template<typename Weight>
   class Edge{
   private:
    //一条边对应两个端点
    int a,b; // 边的两个端点
   Weight weight; // 边的权值
   public:
    // 构造函数
   Edge(int a, int b, Weight weight){
        this->a = a;
        this->b = b;
        this->weight = weight;
   }
    // 空的构造函数, 所有的成员变量都取默认值
   Edge(){}
   //析构函数
   ~Edge(){}

   成员函数

   int v(){
      return a;    // 返回第一个顶点
    }     
   int w(){
      return b;    // 返回第二个顶点
   }      
   Weight wt(){      // 返回权值
      return weight;
    }   
   
    // 给定一个顶点, 返回另一个顶点
    //other(int x）在图的算法中常用
   int other(int x){
      assert( x == a || x == b );
      return x == a ? b : a;
   }

   在图中，我们会经常对对象进行运算符操作，所以在这里需要使用运算符的重载，如下：

   // 输出边的信息
   friend ostream& operator<<(ostream &os, const Edge &e){
          os<<e.a<<"-"<<e.b<<": "<<e.weight;
          return os;
   }
   // 边的大小比较, 是对边的权值的大小比较
   bool operator<(Edge<Weight>& e){
          return weight < e.wt();
   }
    bool operator<=(Edge<Weight>& e){
          return weight <= e.wt();
   }
    bool operator>(Edge<Weight>& e){
          return weight > e.wt();
   }
    bool operator>=(Edge<Weight>& e){
          return weight >= e.wt();
   }
    bool operator==(Edge<Weight>& e){
          return weight == e.wt();
    }
   };

2. 稀疏图(邻接表)的实现
   在带权图中，我们需要将Edge的类的头文件引入

   #include <iostream>
   #include <vector>
   #include <cassert>
   #include "Edge.h"

   需要将原来的数据类型int类型改为:<Edge<Weight>*>类型,如下：
   vector<vector<Edge<Weight> *> > g;

   
   using namespace std;
   // 稀疏图 - 邻接表
   template<typename Weight>
   class SparseGraph{
   private:
   int n, m; // 节点数和边数
   bool directed; // 是否为有向图
   vector<vector<Edge<Weight> *> > g; // 图的具体数据

   public:
   // 构造函数
   //传入节点个数和是否为有向图
   SparseGraph( int n , bool directed){
      assert(n >= 0);
      this->n = n;
      this->m = 0; // 初始化没有任何边
      this->directed = directed;
     // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
      g = vector<vector<Edge<Weight> *> >(n, vector<Edge<Weight> *>());
   }
   
   // 析构函数
   ~SparseGraph(){
      for( int i = 0 ; i < n ; i ++ )
          for( int j = 0 ; j < g[i].size() ; j ++ )
              delete g[i][j];
   }
   

   成员函数

   int V(){ return n;} // 返回节点个数
   int E(){ return m;} // 返回边的个数
   
   // 向图中添加一个边, 权值为weight
   void addEdge( int v, int w , Weight weight){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
   
        // 注意, 由于在邻接表的情况, 查找是否有重边需要遍历整个链表
        // 我们的程序允许重边的出现
        //需要开空间，Edge<Weight>类型,包括：两个节点和权值
        g[v].push_back(new Edge<Weight>(v, w, weight));
        if( v != w && !directed )
              g[w].push_back(new Edge<Weight>(w, v, weight));
        m ++;
   }
   // 验证图中是否有从v到w的边
   bool hasEdge( int v , int w ){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
        for( int i = 0 ; i < g[v].size() ; i ++ ){
               if( g[v][i]->other(v) == w ){
                   return true;
               }
               return false;
        }
   }
   
   // 显示图的信息
   void show(){
   
       for( int i = 0 ; i < n ; i ++ ){
           cout<<"vertex "<<i<<":\t";
           for( int j = 0 ; j < g[i].size() ; j ++ )
                 cout<<"( to:"<<g[i][j]->w()<<",wt:"<<g[i][j]->wt()<<")\t";
           cout<<endl;
       }
   }

   • 下面来看看稀疏图的迭代器
     其实和前面一样, 将原来的int类型改为Edge<Weight>*

     // 邻边迭代器, 传入一个图和一个顶点,
     // 迭代在这个图中和这个顶点向连的所有边  
     class adjIterator{
     private:
      SparseGraph &G; // 图G的引用
      int v;
      int index;
     public:
      // 构造函数
      //传入图和一个节点
      adjIterator(SparseGraph &graph, int v): G(graph){
           this->v = v;
           this->index = 0;
     }
      //析构函数
      ~adjIterator(){}
     
      // 返回图G中与顶点v相连接的第一个边
     Edge<Weight>* begin(){
           index = 0;
           if( G.g[v].size() )
                return G.g[v][index];
     // 若没有顶点和v相连接, 则返回NULL
           return NULL;
     }
     // 返回图G中与顶点v相连接的下一个边
     Edge<Weight>* next(){
          index += 1;
          if( index < G.g[v].size() )
              return G.g[v][index];
           return NULL;
     }
     
      // 查看是否已经迭代完了图G中与顶点v相连接的所有顶点
      bool end(){
            return index >= G.g[v].size();
       }
      };
     };

3. 稠密图—邻接矩阵的实现
   同样需要将Edge类的头文件引入

   #include <iostream>
   #include <vector>
   #include <cassert>
   #include "Edge.h"
   using namespace std;

   编写一个类
   同理，需要将原来的bool类型改为Edge<Weight> *

   // 稠密图 - 邻接矩阵
   template <typename Weight>
   class DenseGraph{
   private:
      int n, m; // 节点数和边数
      bool directed; // 是否为有向图
      vector<vector<Edge<Weight> *>> g; // 图的具体数据
   public:
    // 构造函数
   DenseGraph( int n , bool directed){
        assert( n >= 0 );
        this->n = n;
        this->m = 0;
        this->directed = directed;
       // g初始化为n*n的矩阵, 每一个g[i][j]指向一个边的信息, 初始化为NULL
         g = vector<vector<Edge<Weight> *>>(n, vector<Edge<Weight> *>(n, NULL));
   }
   
    // 析构函数
   ~DenseGraph(){
   
        for( int i = 0 ; i < n ; i ++ )
            for( int j = 0 ; j < n ; j ++ )
                if( g[i][j] != NULL )
                    delete g[i][j];
   }

   成员函数：

   int V(){ return n;} // 返回节点个数
   int E(){ return m;} // 返回边的个数
   // 向图中添加一个边, 权值为weight
   void addEdge( int v, int w , Weight weight ){
         assert( v >= 0 && v < n );
         assert( w >= 0 && w < n );
   
     // 如果从v到w已经有边, 删除这条边
         if( hasEdge( v , w  ) ){
               delete g[v][w];
               if( v != w && !directed ){
                   delete g[w][v];
               }
               m --;
         }
   
        g[v][w] = new Edge<Weight>(v, w, weight);
        if( v != w && !directed ){
               g[w][v] = new Edge<Weight>(w, v, weight);
        }
        m ++;
   }
   // 验证图中是否有从v到w的边
   bool hasEdge( int v , int w ){
       assert( v >= 0 && v < n );
       assert( w >= 0 && w < n );
       return g[v][w] != NULL;
   }
   // 显示图的信息
   void show(){
       for( int i = 0 ; i < n ; i ++ ){
          for( int j = 0 ; j < n ; j ++ ){
              if( g[i][j] ){
                  cout<<g[i][j]->wt()<<"\t";
              }
              else 
                  cout<<"NULL\t";
          cout<<endl;
          }
     }
   }

• 稠密图迭代器的实现
  在迭代器中只需要把原来的bool类型改为Edge<Weight>*

// 邻边迭代器, 传入一个图和一个顶点,
// 迭代在这个图中和这个顶点向连的所有边
class adjIterator{
private:
    DenseGraph &G; // 图G的引用
    int v;
    int index;

public:
    // 构造函数
  adjIterator(DenseGraph &graph, int v): G(graph){
        this->v = v;
        this->index = -1; // 索引从-1开始, 因为每次遍历都需要调用一次next()
  }

    ~adjIterator(){}

// 返回图G中与顶点v相连接的第一个边
  Edge<Weight>* begin(){
            // 索引从-1开始, 因为每次遍历都需要调用一次next()
  index = -1;
 return next();
  }

        // 返回图G中与顶点v相连接的下一个边
  Edge<Weight>* next(){
        // 从当前index开始向后搜索, 直到找到一个g[v][index]为true
       for( index += 1 ; index < G.V() ; index ++ ){
              if( G.g[v][index] )
                    return G.g[v][index];
              // 若没有顶点和v相连接, 则返回NULL
              return NULL;
      }
  }

        // 查看是否已经迭代完了图G中与顶点v相连接的所有边
  bool end(){
            return index >= G.V();
    }
  };
};

本作品采用《CC 协议》，转载必须注明作者和本文链接