最小生成树之prim算法

一、prim算法

最小生成树prim版，是由prim提出的
在prim的实现中，需要使用辅助数据结构——最小堆，将所有的横切边放入最小堆中，经过一系列操作后取堆顶元素，就可得到最小生成树。
其思想是基于切分定理，其过程如下：
如下图，初始时，全为蓝色，当某个节点被访问到时，就将其标记(实现中用marked数组标记，标记后即为红色）：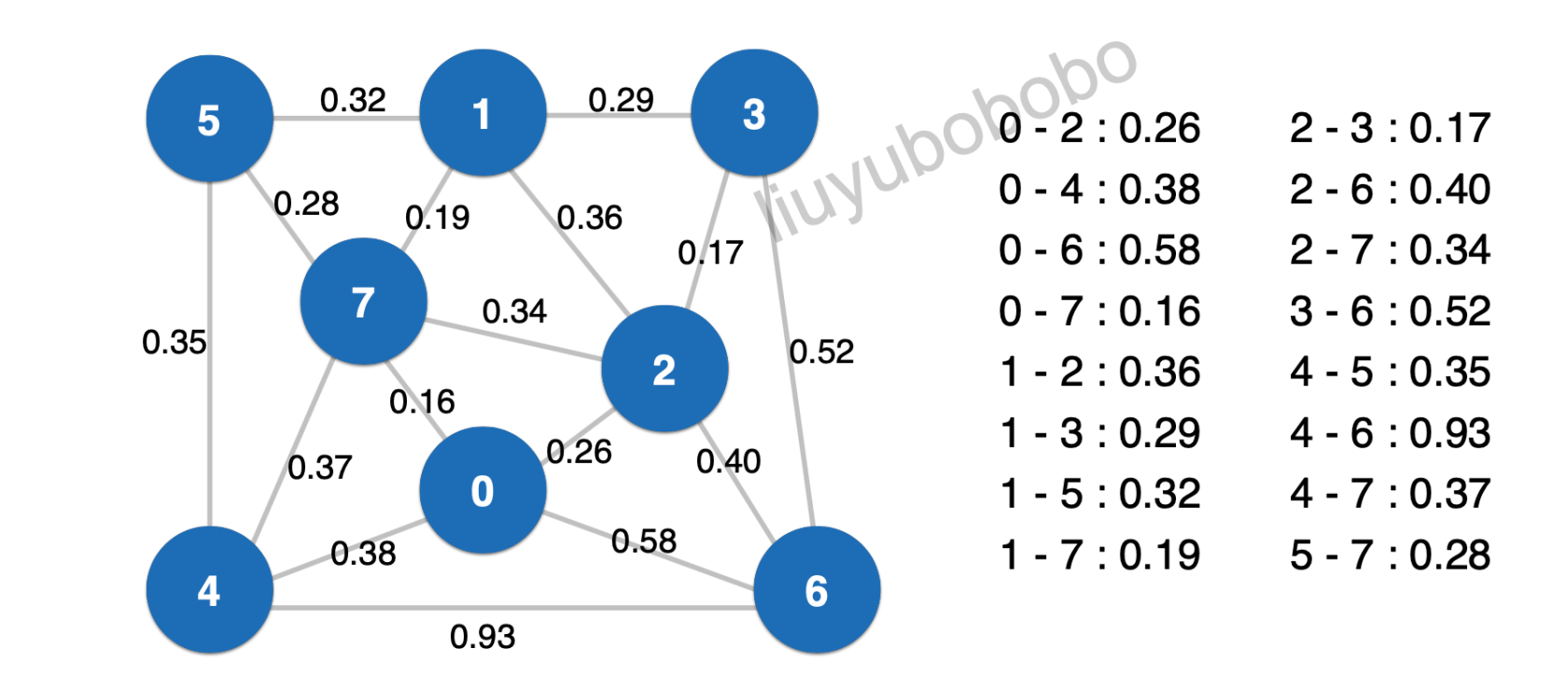

从0开始: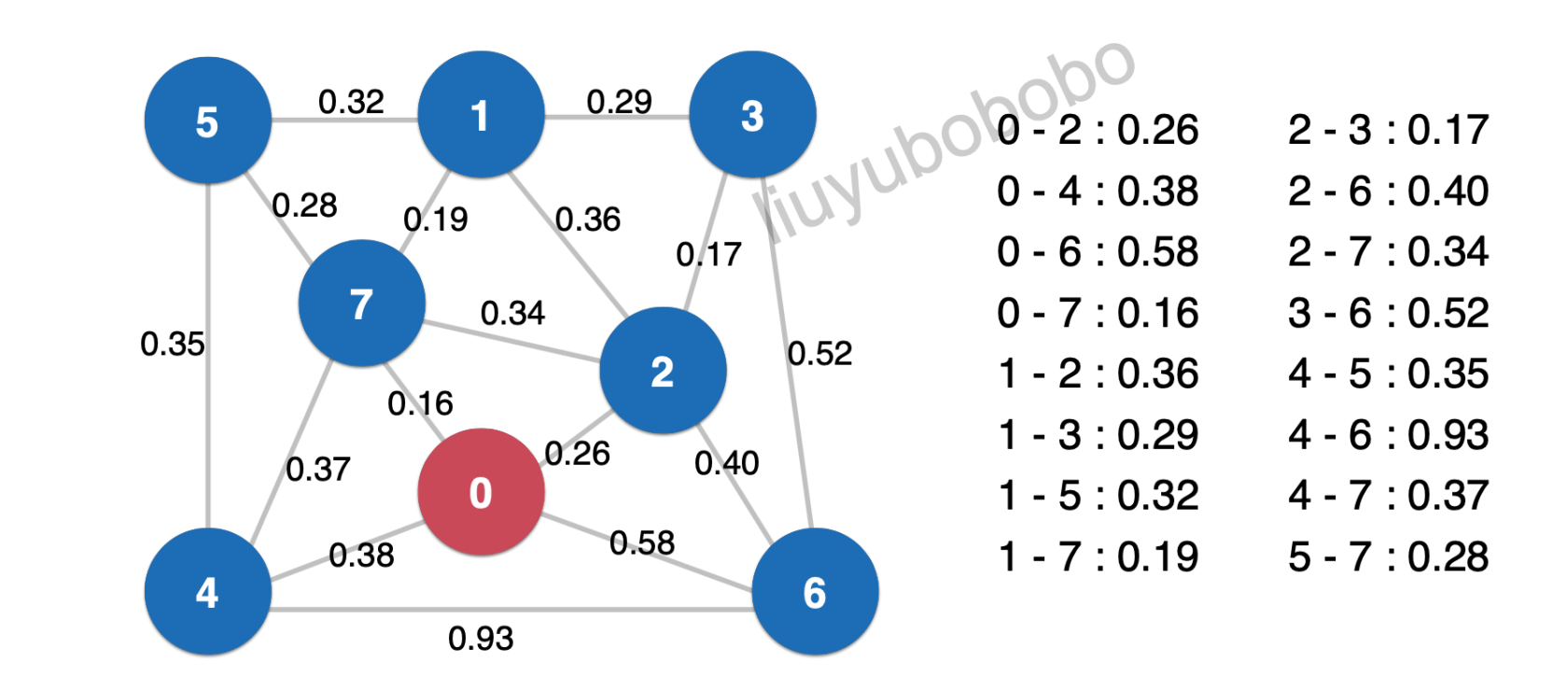

将对应的横切边放入堆中

此时从最小堆中取堆顶元素0.16出来，0.16就属于最小生成树中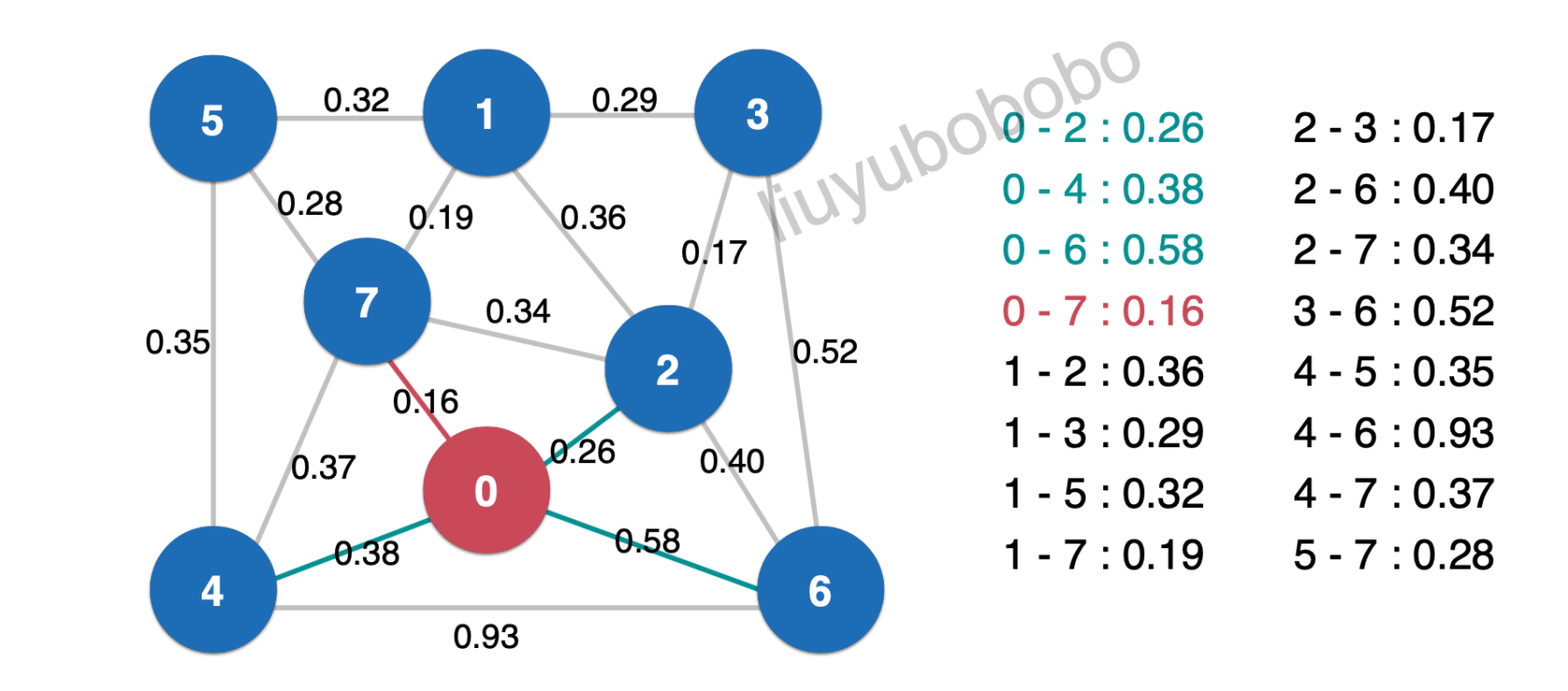

然后将最小生成树中的边0.16相连的未被访问节点加入红色

再将新产生的横切边放入最小堆中：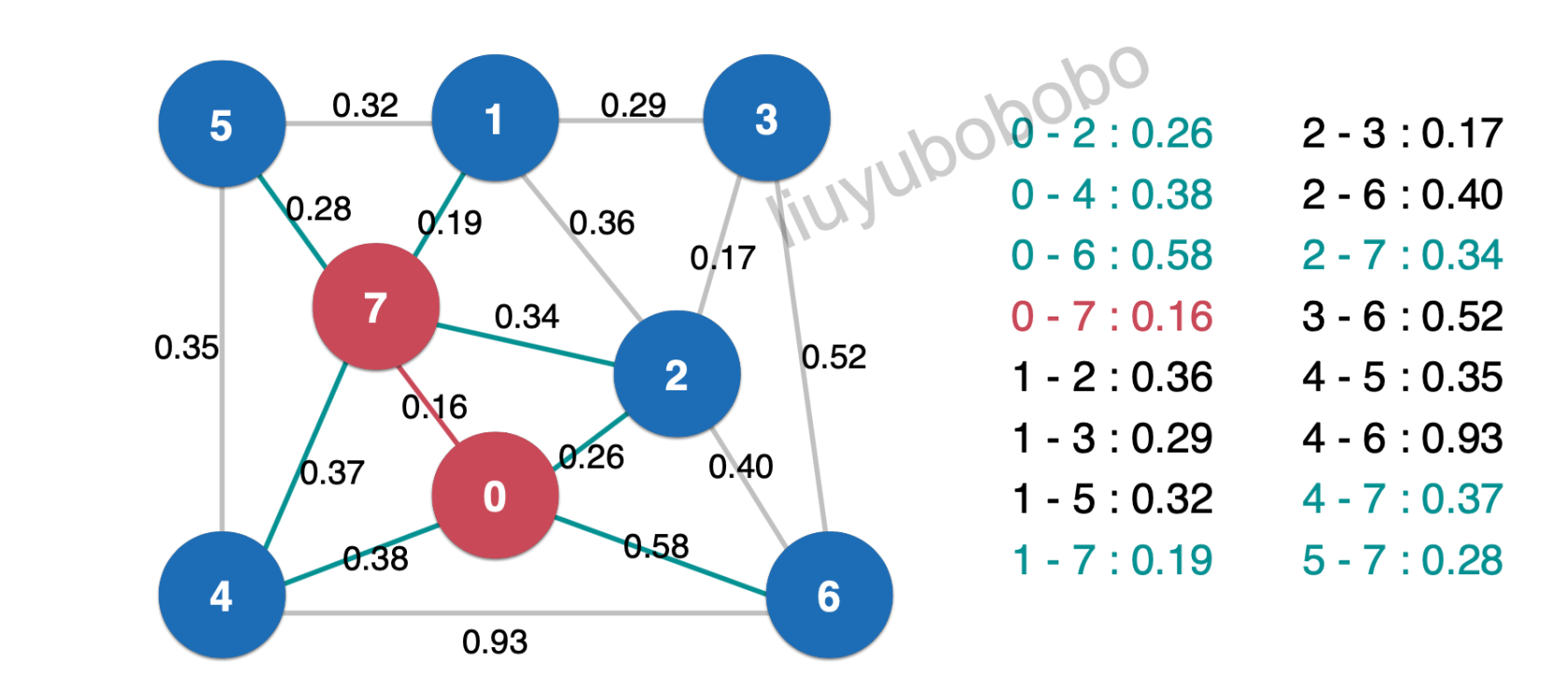

此时再次将堆顶元素0.19取出，加入最小生成树中：

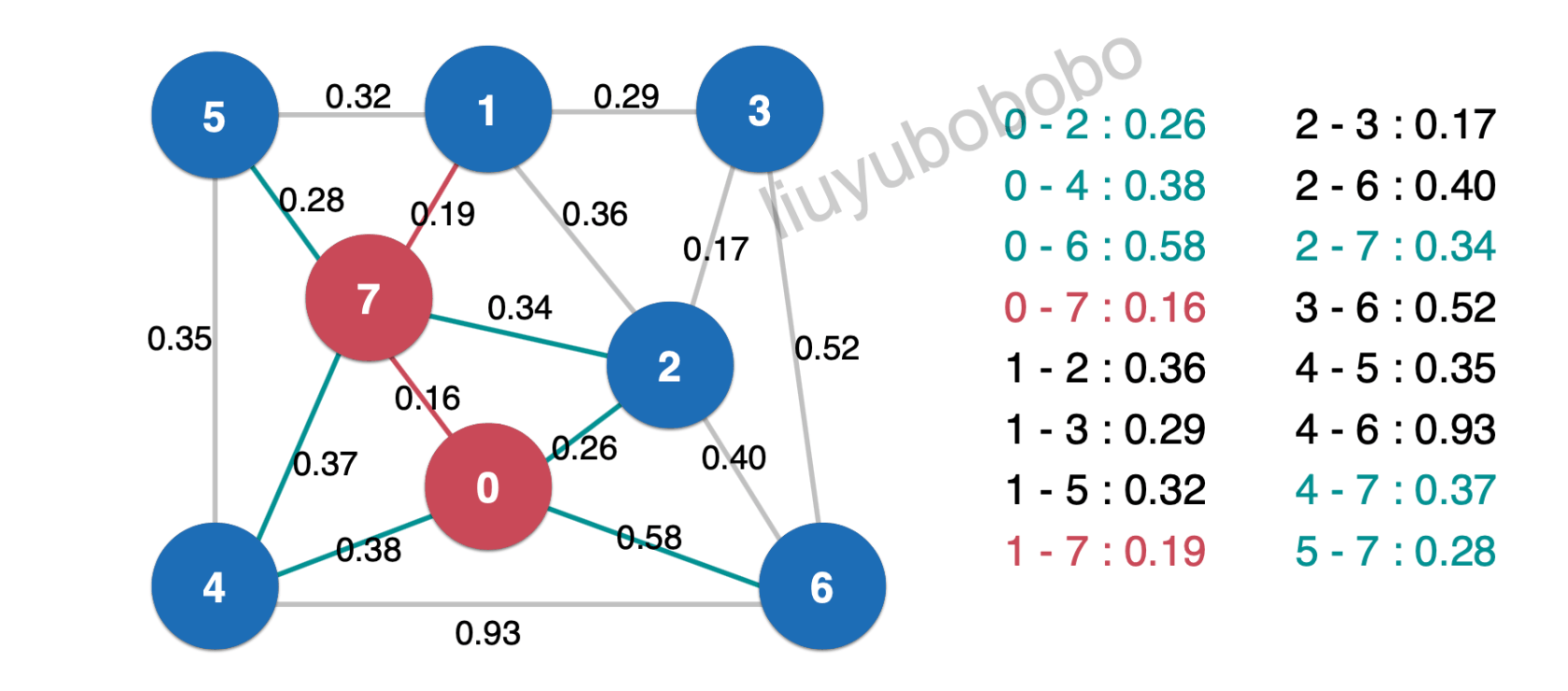
然后再将最小生成树中的边0.19相连的未被访问节点加入红色：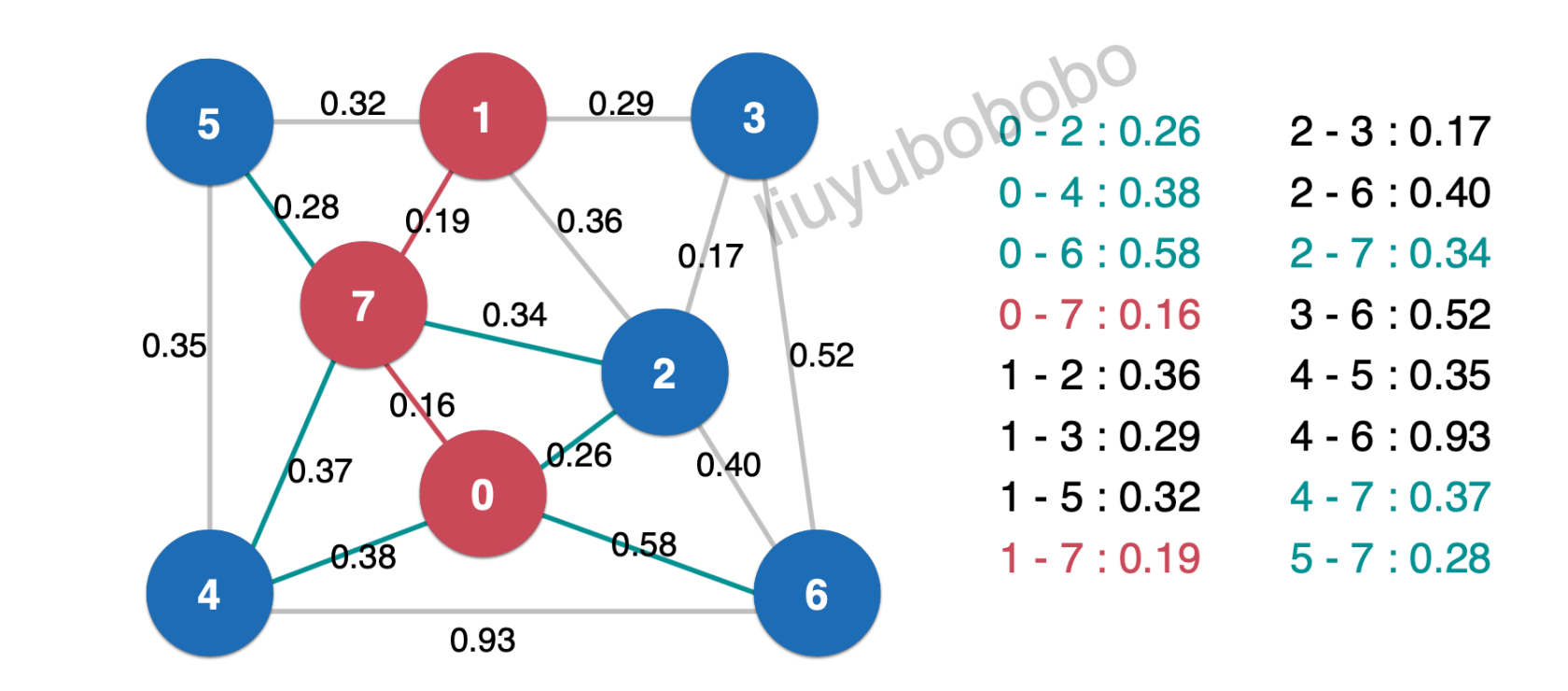

有一次将新产生的横切边加入最小堆中：

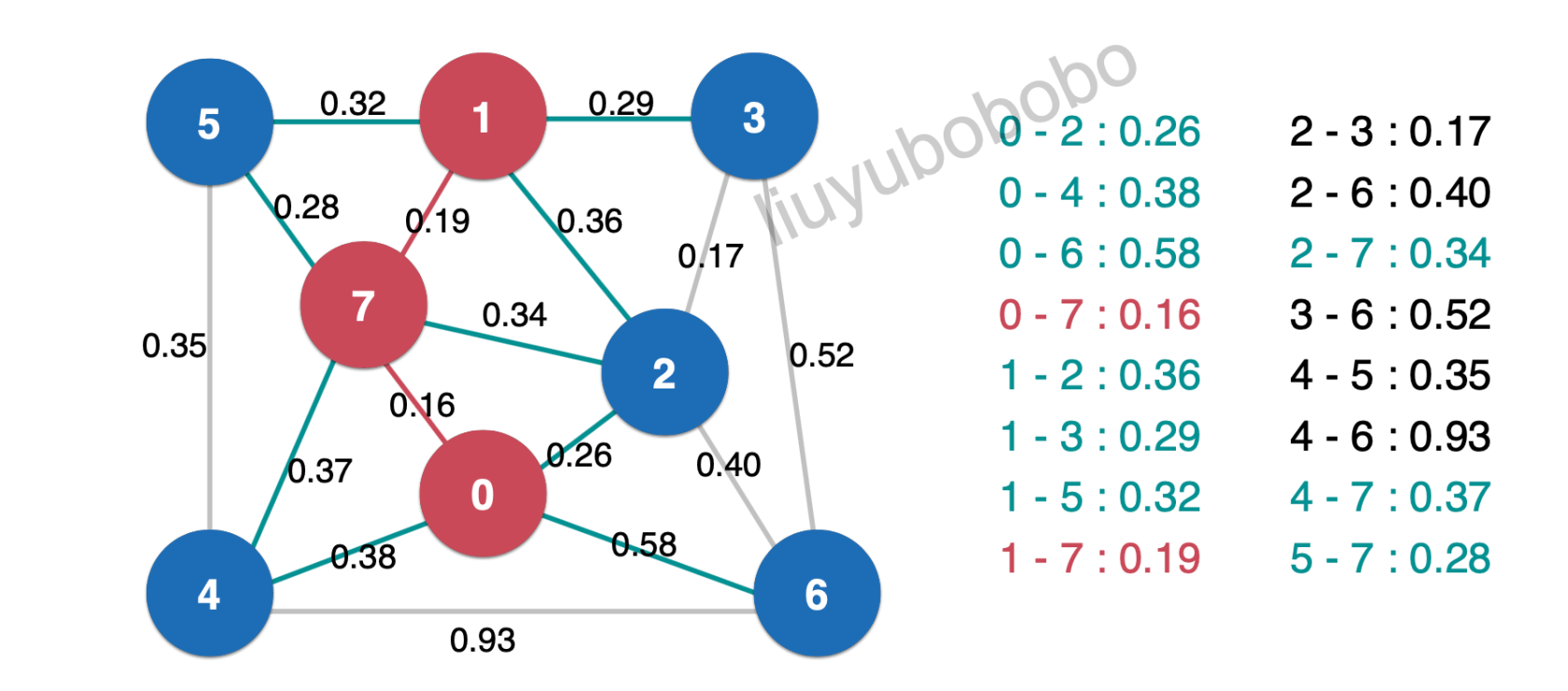
再一次取出堆顶元素0.26：

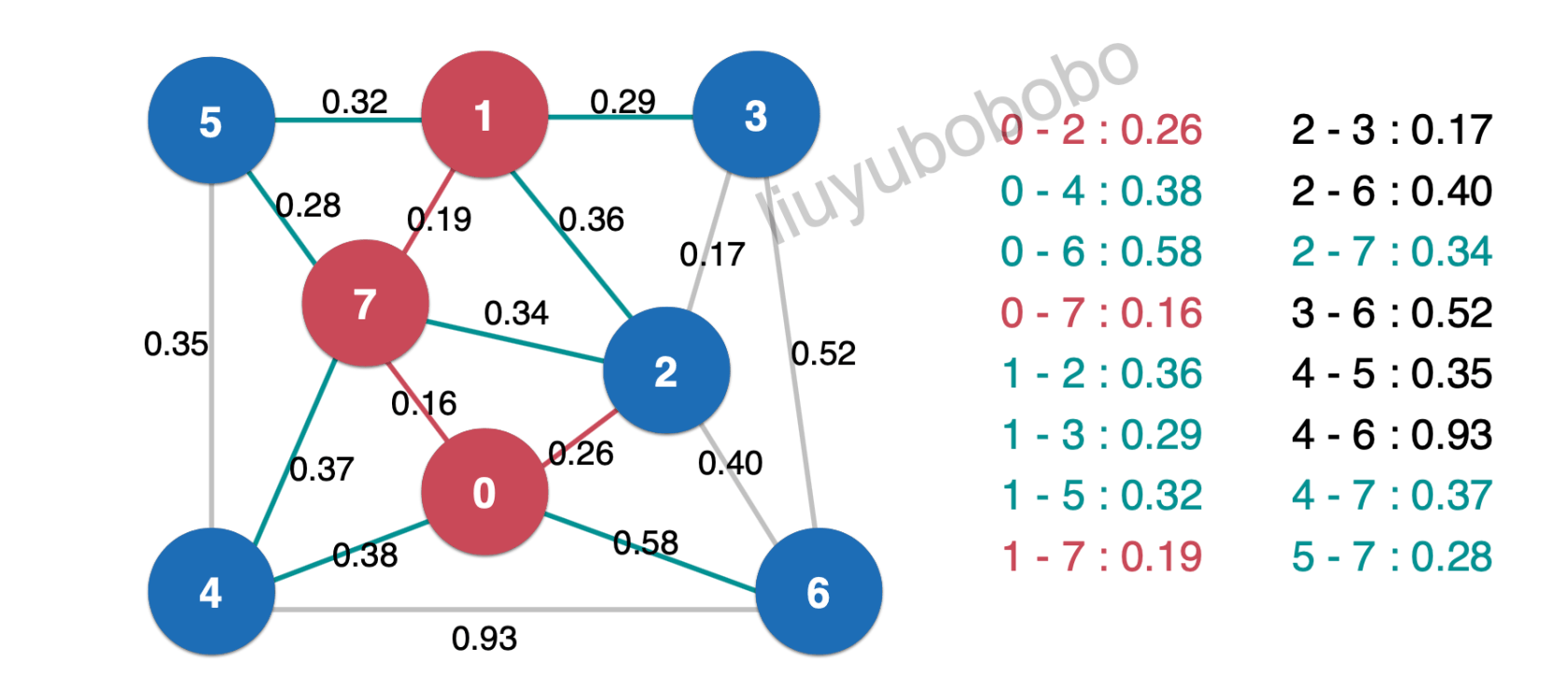
然后将最小生成树中的边0。26相连的未被访问节点加入红色，并将新产生的横切边放入最小堆中：

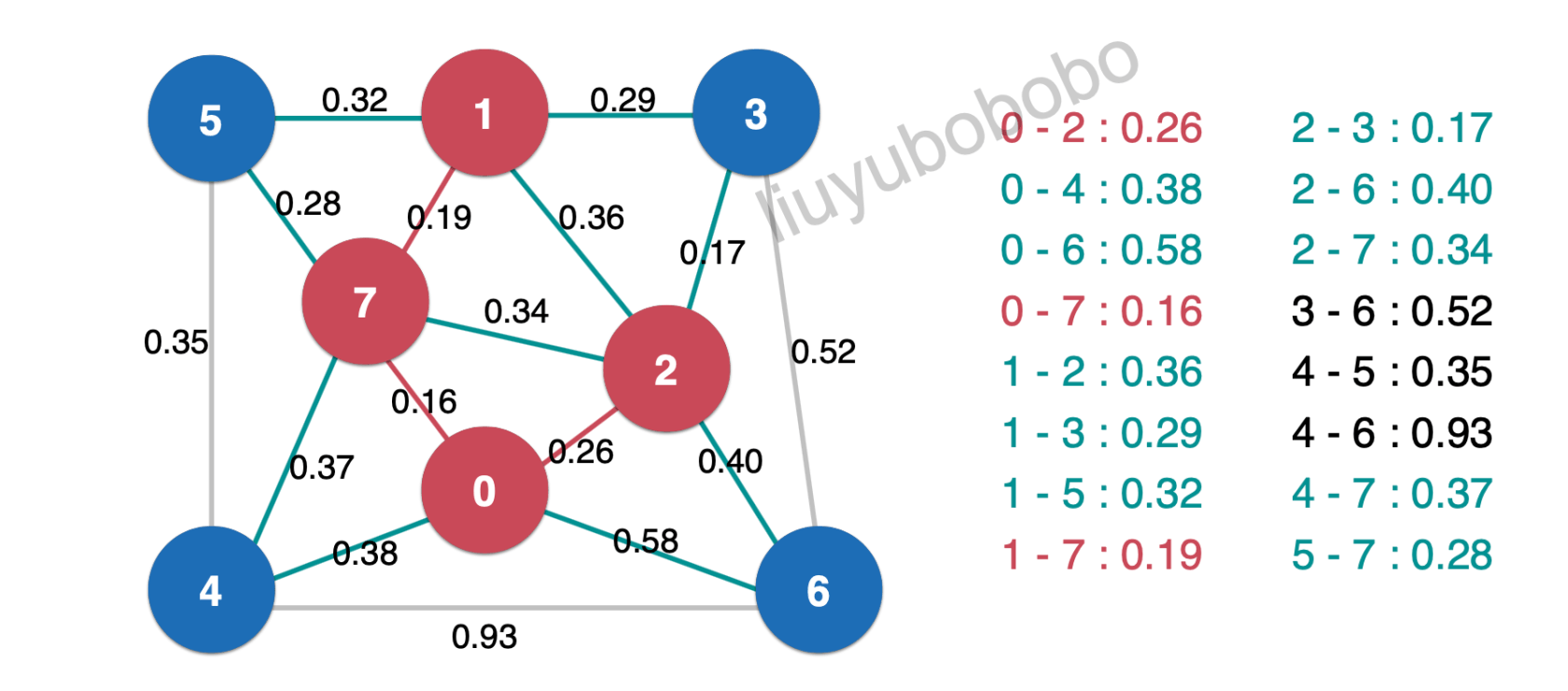
再一次取出堆顶元素0.17，加入最小生成树中：

然后将最小生成树中的边0.17相连的未被访问节点加入红色，并将新产生的横切边放入最小堆中：

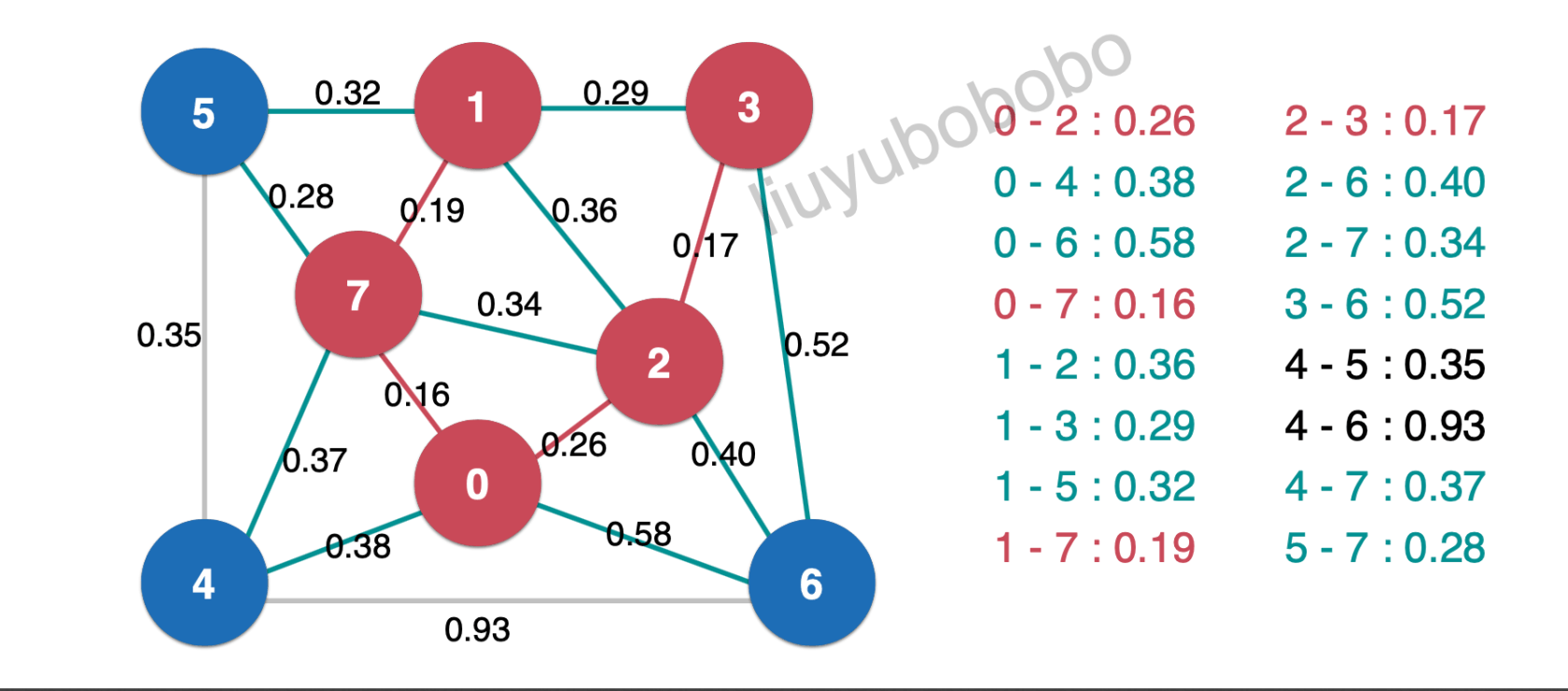
再一次取出堆顶元素0.28，加入最小生成树中：

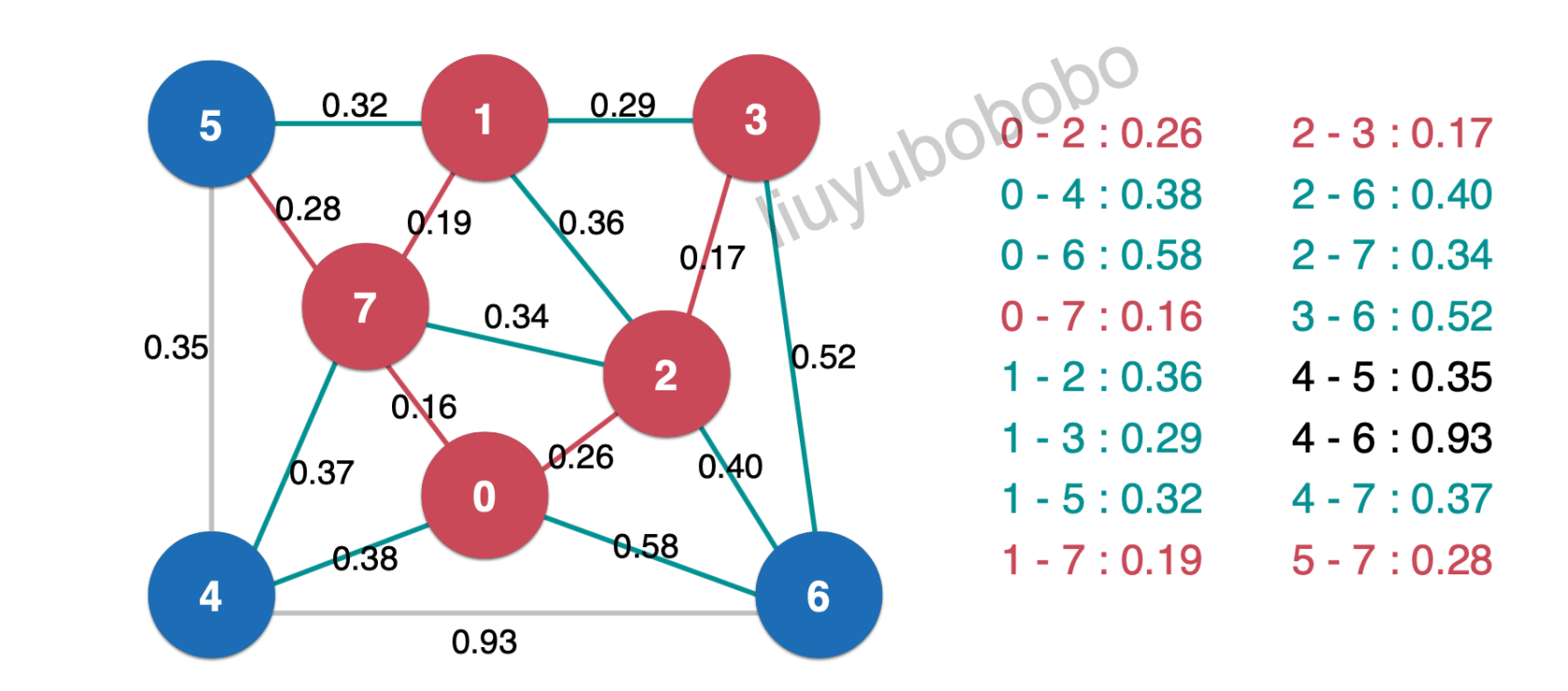
然后将最小生成树中的边0.28相连的未被访问节点加入红色，并将新产生的横切边放入最小堆中：

再一次取出堆顶元素0.29，（注意：此时边0.29它已经不满足横切边了(0.29的两端都为红色阵营)，但是边0.29仍然在最小堆中且为堆顶元素，此时在代码中需要加入判断语句：if( marked[1] != marked[3] )，取出的边判断是不是横切边，不是则扔掉，是则加入最小生成树中。）0.29直接扔掉。进入下一轮：

取出0.32，直接扔掉：

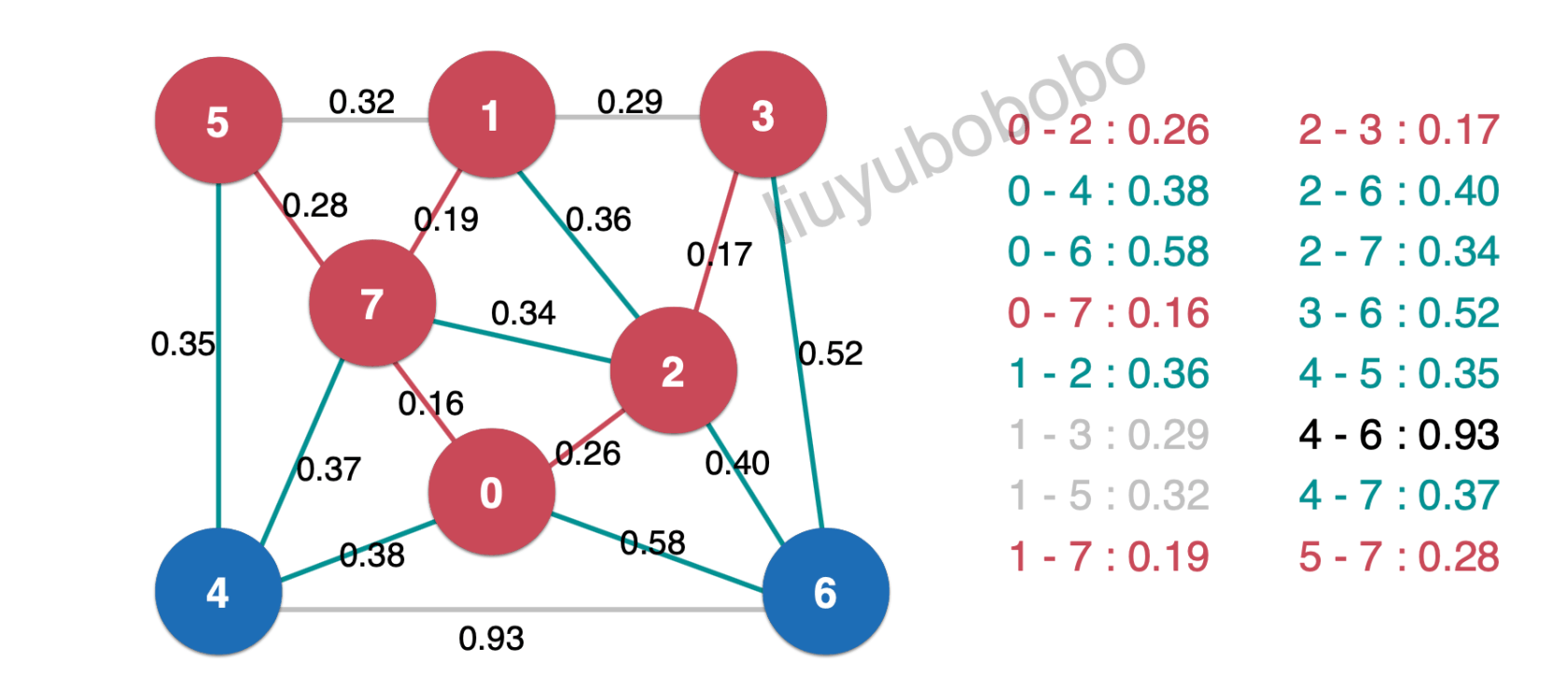
取出0.34，直接扔掉：

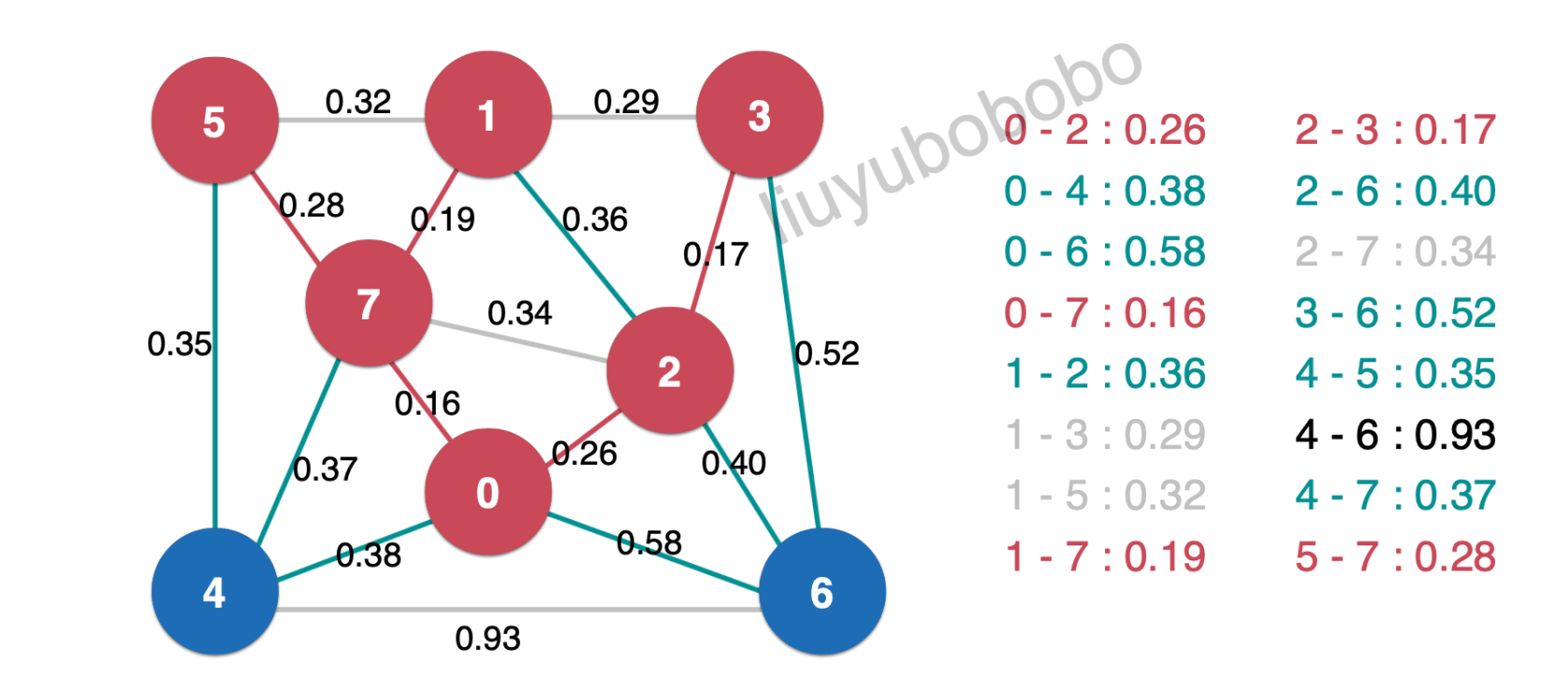
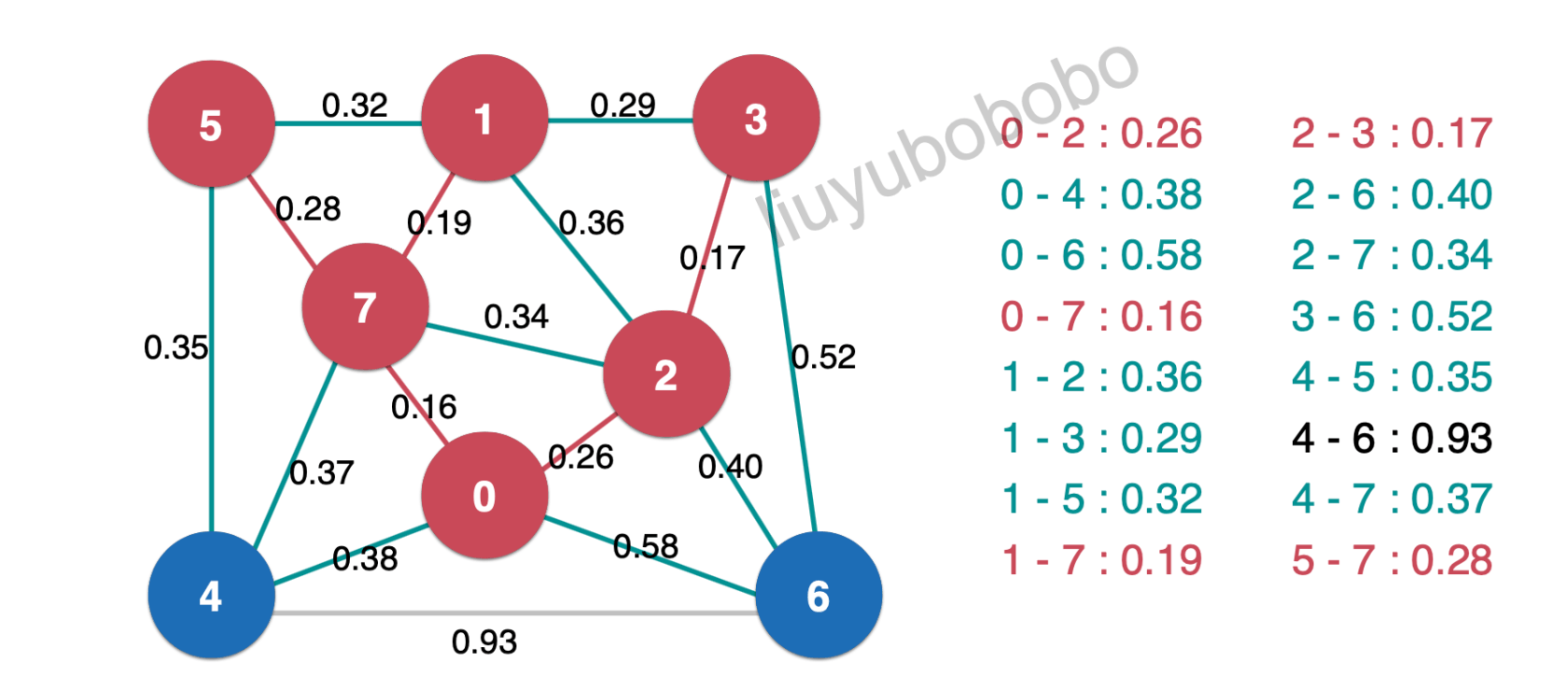
取出0.35，加入最小生成树中，并将最小生成树中的边0.35相连的未被访问节点加入红色，再将新产生的横切边放入最小堆中：

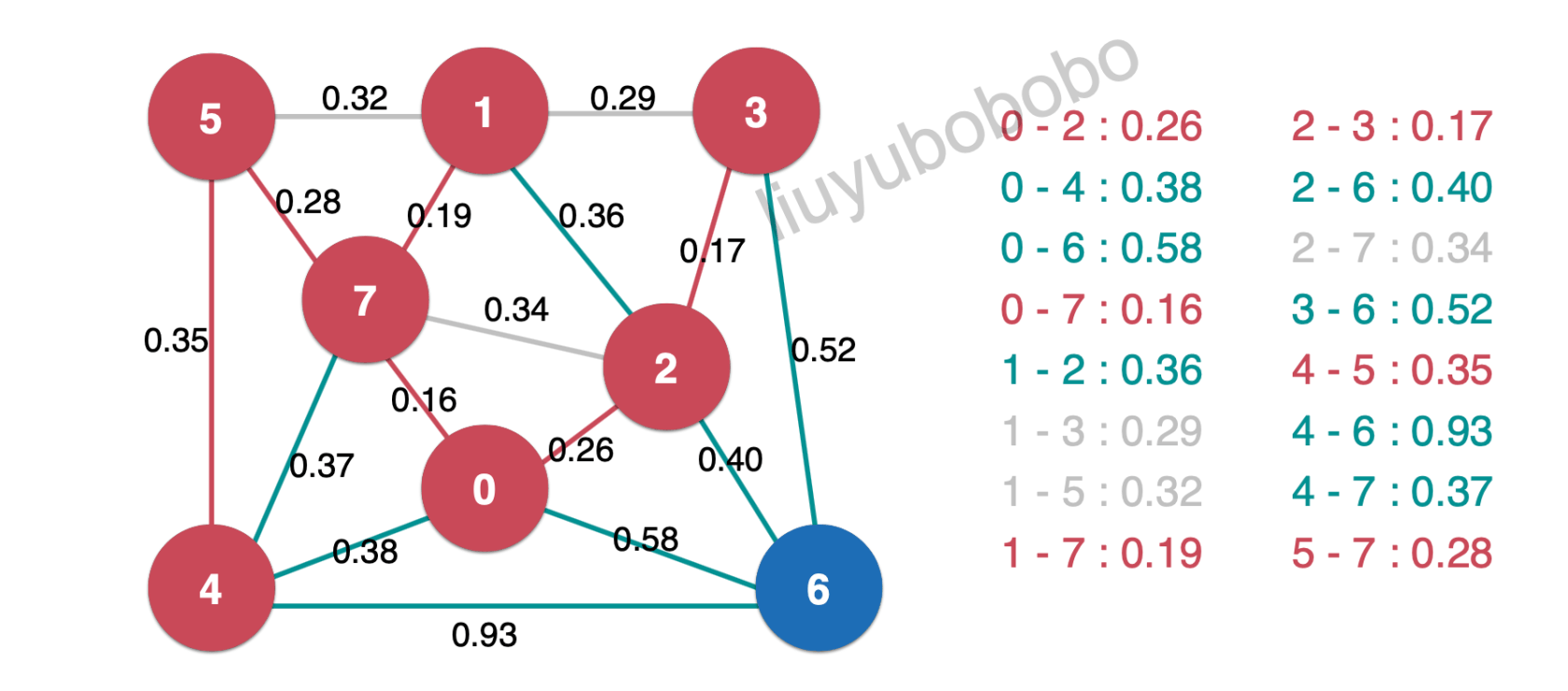
然后依次取出0.36 、0.37，0.38直接扔掉；再取出最小堆堆顶元素0.40，加入最小生成树中；并将最小生成树中的边0.40相连的未被访问节点加入红色，再将新产生的横切边放入最小堆中：

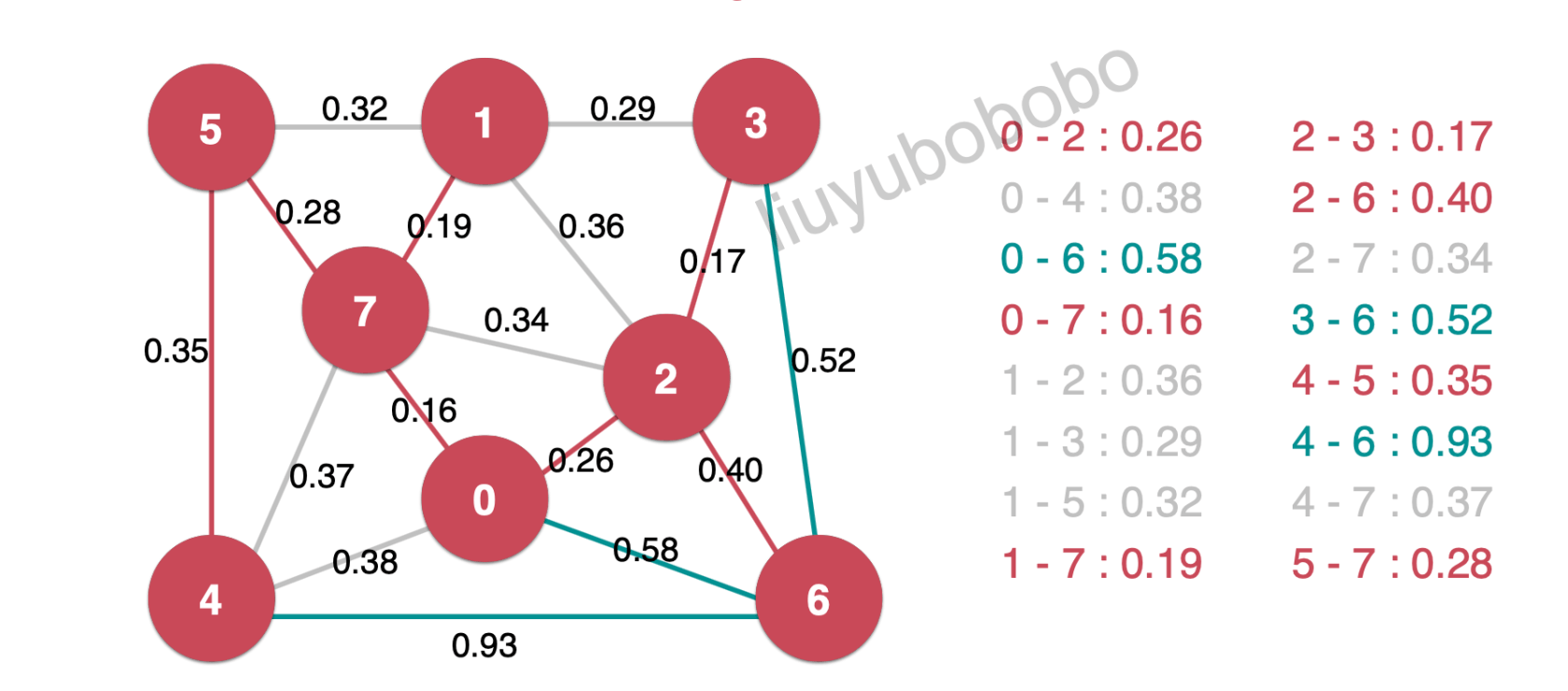
然后在依次取出堆顶元素0.52、0.58、0.93，直到最小堆为空。

二、prim最小生成树的实现

需要一个辅助数据结构——最小堆

#include <algorithm>
#include <cassert>

using namespace std;

//最小堆
template <typename Item>
class MinHeap{

private:
    Item *data; //原始数据对应的数组
    int count; //数据对应的索引
    int capacity;  //堆中容量

    void shiftUp(int k){
          while(k > 1 && data[k] < data[k/2]){
              swap(data[k]), data[k/2];
              k /= 2;
          }
      }

    void shiftDown(int k){
        while(2*k <= count){
            int j = 2*k;
            //右孩子存在
            if(j+1 < count && data[j] > data[j+1]) {
                j++;
            }
            //右孩子不存在
            if(data[k] <= data[j]){
                break;
            }
            swap(data[k], data[j]);
            k = j;
   }
 }

 public:
    //构造函数，构造一个空堆可容纳capacity个元素
     MinHeap(int capacity ){

          data = new Item[capacity + 1]; //开capacity+1的空间，对应第一个元素从索引值1开始
          count = 0;
          this->capacity = capacity;

  }
         //构造函数，通过给定一个定数组创建一个最小堆
     MinHeap(Item arr[], int n){
          data = new Item[n+1];
          capacity = n;

          for(int i = 0; i < n; i++){
              data[i+1] = arr[i];
          }
          count = n;
 }

    //析构函数
  ~MinHeap(){
        delete[] data;
  }

  //返回堆中的元素个数
  int size(){
      return count;
  }

  //返回一个布尔值，表示堆是否为空
  bool isEmpty(){
      return count == 0;
  }

  //向最小堆中，插入一个新元素item
  Item insert(Item item){
      assert(count + 1 <= capacity);
      data[count+1] = item;
      shiftUp(count+1);
      count ++;

}
  // 从最小堆中取出堆顶元素, 即堆中所存储的最小数据
  Item extracitMin(){
      assert(count > 0);
      Item ret = data[1];
      swap(data[1], data[count]);

      count --;
      shiftDown(1);
      return ret;
  }

  //查看堆顶元素
  Item getMin(){
      assert(count > 0);
      return data[1];
 }
};

prim最小生成树

引入头文件：

#include <iostream>
#include <cassert>
#include <vector>
#include "Edge.h"
#include "MinHeap.h"

//使用LazePrim算法求最小生成树
using namespace std;

//使用prim算法求图的最小生成数
template <typename Graph, typename Weight>

class LazePrimMST {
private:
    Graph &G;   //图G的引用
    MinHeap<Edge<Weight>> pq;  //最小堆，将横切边放入最小堆中
    bool *marked;              //标记数组，在算法运行过程中标记节点i是否被访问
    vector<Edge<Weight>> mst;  // 最小生成树所包含的所有边
    Weight mstWeight;           // 最小生成树的权值

在private中写visit()方法用来将横切边加入最小堆中：

//visit
void visit(int v) {
    assert(!marked[v]);
    marked[v] = true;

  // 使用图的迭代器，将和节点v相连接的所有未访问的边放入最小堆中
   typename Graph::adjIterator adj(G, v);
   for (Edge<Weight> *e = adj.begin(); !adj.end(); e = adj.next()) {
        //判断v节点的相邻节点是否被访问
        if ( !marked[e->other(v)]) {
              pq.insert(*e);
        }
    }
}

public:
    LazePrimMST(Graph &graph) : G(graph), pq(MinHeap<Edge<Weight>>(graph.E())) {

        //初始化算法
      marked = new bool[G.V()];
      for (int i = 0; i < G.v(); i++) {
            marked[i] = false;
      }
        //将mst清空
      mst.clrar;

      // Prim
      visit(0);
      while (!pq.isEmpty()) {
          // 使用最小堆找出已经访问的边中权值最小的边
          Edge<Weight> e = pq.extracitMin();
          // 如果这条边的两端都已经访问过了, 则扔掉这条边
          if (marked[e.v()] == marked[e.w]) {
                continue;
          }
         //否则e就为最小生成树的边
          mst.push_back(e);

         // 访问和这条边连接的还没有被访问过的节点
         if (!marked[e.v()]) {
              visit(e.v());
         } 
        else {
              visit(e.w);
        }
}

  //计算最小生成树的权值
       mstWeight = mst[0].wt;
       for (int i = 1; i < mst.size(); i++) {
             mstWeight += mst[i].wt;
       }
}

 //析构函数
  ~LazePrimMST(){
        delete[] marked;
  }

    // 返回最小生成树的所有边
  vector<Edge<Weight>> mstEdge(){
        return mst;
  }

    // 返回最小生成树的权值
  Weight result(){
        return mstWeight;
  }

};

本作品采用《CC 协议》，转载必须注明作者和本文链接