图论之带权图「最小生成树(Minimum Span Tree)」
0 / 0 / 创建于 3年前
iceymoss 的个人博客
图的最小生成树 (Minimum Span Tree)#
一、介绍#
最小生成树：指在一张有 V 个节点和 V-1 条边的图中，V-1 条边连接 V 个节点，所有边的权值之和最小，所形成的树。
如下图：红色的边和所有节点相连所形成的一颗树，就是最小生成树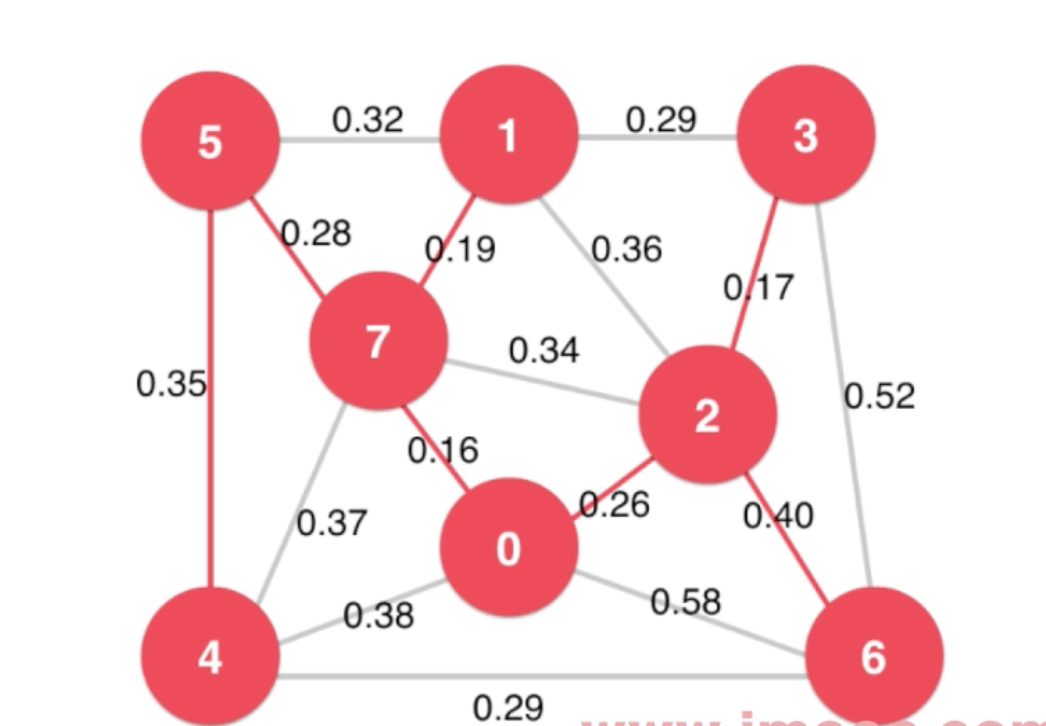
适用范围：
- 带权无向图
- 通常为连通图 (如果有多个不连通的图，则每个子图的最小生成树之和就为最小生成树森林)
二、实际应用#
最小生成树广泛应用于各种场景，如:
- 电缆布线设计
- 网络设计
- 电路设计
- 城市线路规划
- …… 等
三、基于切分定理的最小生成树#
切分定理：指将一张图划分为两个阵营 (这里使用红色阵营和蓝色阵营)，当一条边的 w 节点为红色阵营，v 节点为蓝色阵营，此时的这条边就属于横切边。
实例：如下图
如下，横切边就有：
0.29
0.36
0.34
0.16
0.38
由此可见，给定任意切分，横切边中权值最小的，必然属于最小生成树
下图中 0.16 就属于最小生成树
又如下图中
横切边为：
0.52
0.40
0.58
0.39其中 0.40 属于最小生成树中
由此可见，给定任意切分，横切边中权值最小的，必然属于最小生成树#
本作品采用《CC 协议》，转载必须注明作者和本文链接
关于 LearnKu
粤公网安备 44030502004330号