第四：初高中衔接-绝对值-没有分类法做不出来的绝对值问题，如果有一定是题的问题
0 / 0 / 创建于 2年前 /
wangchunbo 的个人博客
感谢 一数课堂
本节课来自于p4
www.bilibili.com/video/BV147411K7x...
1. 绝对值求。直接判断 大于0 小于0 等于0 的情况
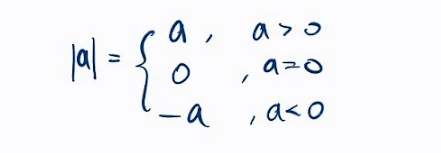
2. 例题与结题思路
求 绝对值 |x-1| > 4
###2.1 分类法： 大于、小于
2.2 几何法。画线段
求 绝对值 |x-1| > 4
则 定点 1. 然后判断。左右 4 个长度的分别是谁。
则只要满足，距离的左右即可
2.3 十字相乘法中应用
分类，x 大于等于0 ，与 x小于0 。然后计算出对应的零点公式。
上面式子的零点。我们已经计算出来了。
则直接画图。即可显而易见。 注意这里，a 都是大于0 ，所以开口是向上的。
所以计算得到：
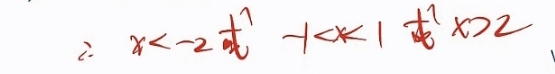
2.4 零点。 取理出来的式子，为0的情况
注意，这里就取零点。 |x-1| 零点1 |x-2| 零点2
所以就计算 两个绝对值的 正负性进行分类。
求解得到：
自己求
2.5 变种题，包含了舍去。
直接分类
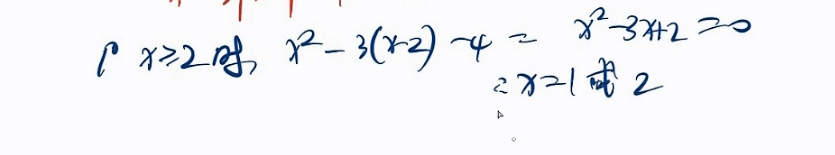
但是。注意这里 x=1 需要舍去。因为x>=2 是前提条件
同理得到x< 2.
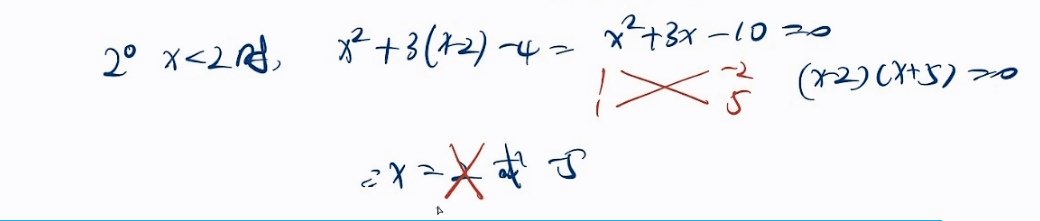
需要舍去 得到的 2.
考试窍门，遇见绝对值就分类!
如果分类都做不出来，那就没方法拉
为甚要记分类法。
如果 例题1 。中 改为 |2x-1| > 4
则 分类法，只要计算 二分之一x大于等于1 分类 与 二分之一x大于小于1分类即可
感想：
这个知识点我记得。哈哈哈哈。
本作品采用《CC 协议》，转载必须注明作者和本文链接
关于 LearnKu
粤公网安备 44030502004330号