让我们一起啃算法----搜索插入位置

搜索插入位置（ Search-Insert-Position ）

题干：

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
  输入: [1,3,5,6], 5
  输入: 输出: 2
示例 3:
  输入: 输入: [1,3,5,6], 7
  输入: 输出: 4
示例 4:
  输入: 输入: [1,3,5,6], 0
  输入: 输出: 0
来源：力扣

这题主要应用 二分查找 的思路来解题，题目是比较简单的，但是二分查找这个思路还是蛮重要的。

解题思路

一般使用二分查找都需要先对原数组进行排序，题中给到的数组是已经排序的，因此这一步可以省去。

二分查找思路比较简单，首先初始化三个指针： left 指向 nums 最左边的元素，right 指向 nums 右边的元素，根据 left 和 right 计算 mid 指针。我们先拿目标值 target 与 nums[mid] 进行比较。

如果 target > nums[mid]，说明要查找的值有可能在 nums[mid+1, right] 之间，这时候将 left 赋值为 mid + 1，right 不变，重新计算一下 mid，重新比较。

如果 target < nums[mid]，说明要查找的值有可能在 nums[left, mid-1] 之间，这时候将 right 赋值为 mid - 1，left 不变，重新计算一下mid，重新比较。

如果 target == nums[mid]，那么恭喜找到啦，根据题意，找到的索引值就是 target 插入的目标位置，即返回 mid 即可。

如果 二分查找结束仍是没有找到 target 的值，最后返回 left 就可以了，至于为什么 left 的值是 target 插入的位置，可以看流程图的分析。

mid 的计算方式： mid = left + ( rigth - left ) / 2，至于为什么不用 ( left + right ) / 2 来计算 mid 是因为 right + left 有可能溢出。
注： ( right - left) / 2 取整，因为数组的索引值是整数。

流程图如下：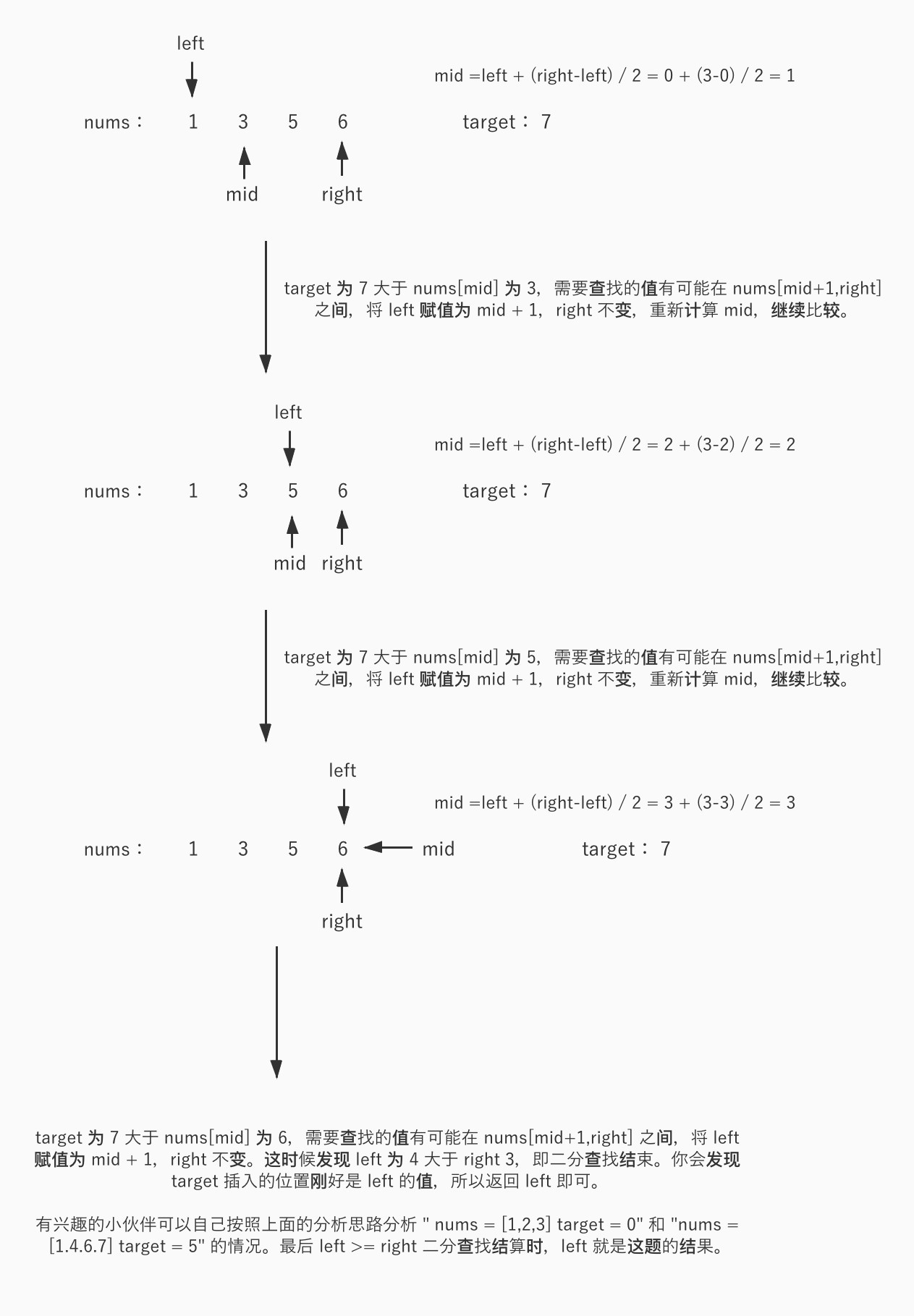

代码实现

// 函数的实现并不是最简洁的，但是整个二分法思路是很清晰的。
func searchInsert(nums []int, target int) int {
    if len(nums) <= 0 {
        return 0
    }

    var left, right = 0, len(nums) - 1
    for left <= right {

        // 根据 left 和 right 计算 mid 的值
        mid := left + (right - left) / 2  // ( left + right ) / 2


        // 目标值大于中间值，left = mid + 1
        if nums[mid] < target {
            left = mid + 1

        // 目标值小于中间值 right = mid - 1
        } else if nums[mid] > target {
            right = mid - 1
        } else {
            // 目标值等于中间值返回 mid，即为目标值需要插入的位置
            return mid
        }
    }

    // 找不到目标值，这时候返回left就是目标值需要插入的位置
    return left

}

总结

每天进步一点点，加油！
算法教程项目，每天更新一题，点个 star 支持一下呀：
https://github.com/wx-satellite/learning-a…

算法数据结构二分查找 leetcode

本作品采用《CC 协议》，转载必须注明作者和本文链接

三斤

三斤和他的喵

课程读者 172 声望

一个PHPer的修行之路。欢迎大家关注我的公众号《三斤和他的喵》

3 人点赞

从小程序个人账户申请开始，带你一步步进行开发一个微信小程序，直到提交微信控制台上线发布。

从零开始带你一步步开发一个 Go 博客项目，让你在最短的时间内学会使用 Go 进行编码。项目结构很大程度上参考了 Laravel。

推荐文章：

更多推荐...

MySQL 8.0 官方手册翻译征集 10 / 14 |

面试 POPER 的后端开发工程师的离奇经历 38 / 104 |

工作

[深圳][15k-20k][双休]PHP后端开发工程师招聘 13 / 39 |

博客

Laravel 实用小技巧 —— 如何快速更新 20 万条 MySQL 数据？ 20 / 26 |

博客

失业两个月找存在感系列——几行代码轻松实现laravel链式追踪，一分钟快速排查系统问题 26 / 19 |

分享创造

📙《高并发的哲学原理》开源图书发布十一天 star 数已经破千！ 48 / 16 |

讨论数量: 4

captain2021

Laravel 5.8 译者 422 声望 / 开发 @ 谈笑风生

function searchInsert($nums, $target) :int {
    if (count($nums) <= 0) {
        return 0;
    }

    $left = 0;
    $right = count($nums) - 1;
    while ($left <= $right) {
        // 根据 left 和 right 计算 mid 的值
        $mid = $left + ($right - $left) / 2; // ( left + right ) / 2

        // 目标值大于中间值，left = mid + 1
        if ($nums[$mid] < $target) {
            $left = $mid + 1;

        // 目标值小于中间值 right = mid - 1
        } else if ($nums[$mid] > $target) {
            $right = $mid - 1;
        } else {
            // 目标值等于中间值返回 mid，即为目标值需要插入的位置
            return $mid;
        }
    }

    // 找不到目标值，这时候返回left就是目标值需要插入的位置
    return $left;
}

return searchInsert([1,4,5,7], 3);  // output:1

5年前评论

三斤和他的喵（楼主）

加油 :wave:

captain2021

Laravel 5.8 译者 422 声望 / 开发 @ 谈笑风生

function searchInsert($nums, $target) {
    $count = count($nums);
    for ($i = 0; $i < $count; $i++) {
        if (isset($nums[$i + 1]) && $nums[$i] < $target && $target <= $nums[$i +1]) {
            return $i + 1;
        }

        if (!isset($nums[$i + 1]) && $nums[$i] < $target) {
            return $i + 1;
        }

        if ($nums[$i] >= $target) {
            return 0;
        }
    }
}

return searchInsert([1,3,5,6], 5); // output: 2

前两天弄得这个，看着更像是实现，不是算法，楼主的二分法还是稳

5年前评论

三斤和他的喵（楼主）

暴力破解 :joy:

captain2021 （作者）

@三斤和他的喵是啊，内存消耗打败 100% 的提交

yzh52521

33 声望

function searchInsert($nums, $target) {
        if (!in_array($target, $nums)) {
            $nums[] = $target;
            sort($nums);

        }
        foreach ($nums as $key => $value) {
            if ($value == $target) {
                return $key;
            }
        }
    }

function searchInsert($nums, $target) {
        $len = count($nums);
        $left = 0;
        $right = $len - 1;
        while ($left <= $right) {
            $mid = (int)(($left + $right) / 2);
            if ($nums[$mid] == $target) {
                return $mid;
            } elseif ($nums[$mid] > $target) {
                $right = $mid - 1;
            } else {
                $left = $mid + 1;
            }
        }
        return $left;
    }

5年前评论

三斤和他的喵（楼主）

优秀 :+1:

取名字好烦。

0 声望

mark

4年前评论

讨论应以学习和精进为目的。请勿发布不友善或者负能量的内容，与人为善，比聪明更重要！

帮助

让我们一起啃算法----搜索插入位置

搜索插入位置（ Search-Insert-Position ）

解题思路

代码实现

总结

推荐文章：

社区赞助商

关于 LearnKu

资源推荐

服务提供商

其他信息

让我们一起啃算法----搜索插入位置

搜索插入位置（ Search-Insert-Position ）

解题思路

代码实现

总结

推荐文章：

社区赞助商

关于 LearnKu

资源推荐

服务提供商

其他信息

请登录