代码随想录算法训练营第十天 | leetcode：滑动窗口最大值,前 K 个高频元素

Problem: 239. 滑动窗口最大值

需要注意的地方

* !!!以下内容为PHP手册的一些翻译!!!
* 1) pop() & push()继承自SplDoublyLinkedList，可以应用于SplStack以及SplQueue(即“无脸”)。它与堆栈或队列无关;它只是关于删除/添加元素到列表的末尾;
* 2) 与shift()和unshift()相同的情况:它只是将一个元素添加到列表的开头，如果我们在SplStack或SplQueue上使用它并不重要。
*   所以，是的，$q->pop();将从SplQueue $q中删除*last*元素。
* 3) 但是enqueue()和dequeue() *是关于* SplQueue的。FIFO原理是由这些方法实现的，这些方法都是为了队列目的而实现的:
*    enqueue()将一个元素添加到队列的末尾
*    dequeue()从队列的开头删除元素
* 4) 如果你想从*queue*中删除*下一行*元素，使用dequeue()。
*    如果你想从列表中删除最后一个元素(不管它是队列还是堆栈)，使用pop()。
*    如前所述，SplQueue对象上的push()和pop()方法的行为更像是堆栈而不是队列。
* 5) 知道enqueue()和dequeue()方法分别是push()和shift()方法的别名，
*    我们也可以使用SplQueue:: push()和SplQueue:: shift()来达到与SplQueue:: enqueue和SplQueue:: dequeue相同的目的。

简而言之,需要注意的地方是《SplQueue 类》因为继承自SplDoublyLinkedList的原因，继承的一些方法特性更像栈而不是队列，比如：top指向队列队尾，bottom才是指向队头。
什么是单调队列。队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。那么这个维护元素单调递减的队列就叫做单调队列，即单调递减或单调递增的队列。那么这个维护元素单调递减的队列就叫做单调队列

解题方法

需要设计一个单调队列，分别实现pop(),push(),getMax()方法；

单调队列中push()的逻辑：在入队列的时候，依次与队尾的元素做比较，比要入队列的元素小的则从队尾pop()弹出来。直到找到大于等于自身的元素。然后入队列。也就是一个排序的过程，只不过不需要维护所有元素。
单调队列中pop()的逻辑：根据窗口的移动，dequeue()弹出队头的元素。
单调队列中getMax()的逻辑：经过push的筛选，队头的元素已经是最大的元素。所以直接返回队头元素即可。
以题目示例为例，输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3，动画如下：

复杂度

时间复杂度:

O(n)

空间复杂度:

O(k)

code

 class Solution {

    private $singleQueue;

    /**
     * @param Integer[] $nums
     * @param Integer $k
     * @return Integer[]
     */
    function maxSlidingWindow($nums, $k) {
        if (count($nums) == 1|| $k == 1) return $nums;

        $this->singleQueue = new SplQueue();
        // 先将前k的元素放进队列
        for ($i = 0; $i < $k; $i++) {
            $this->singlePush($nums[$i]);
        }
        $result = [];
        $result[] = $this->getMax(); // result 记录前k的元素的最大值
        //先将前k个数据push进数组中，后续当$i++ 后移时就可以统一记录最大值
        for ($i = $k; $i < count($nums); $i++) {
            // 滑动窗口移除最前面元素
            $this->singlePop($nums[$i - $k]); 
            // 滑动窗口前加入最后面的元素
            $this->singlePush($nums[$i]); 
            // 记录对应的最大值
            $result[]= $this->getMax(); 
        }
        return $result;
    }
     function singlePop($val){
         //$this->singleQueue继承自SplDoublyLinkedList，所以更像栈，由于栈的头尾与队列头尾相反，所以使用继承方法时，需要注意头尾方向。
         // 滑动窗口移除最前面元素时，需要判断是否等于最大值，如果不等于，那么不用移除，因为在push的时候已经被筛选掉了
         if(!$this->singleQueue->isEmpty() && $this->singleQueue->bottom() == $val){
            $this->singleQueue->dequeue();
         }
     }

     function singlePush($val){
         //判断队列尾部元素是否小于准备入队列元素，是则从尾部弹出，直到大于等于队列尾部元素，然后入队列
         while(!$this->singleQueue->isEmpty() && $this->singleQueue->top() < $val){
             //从队列尾部弹出元素
             $this->singleQueue->pop();
         }
         $this->singleQueue->enqueue($val);
     }

     function getMax(){
         //经过singlePush筛选，队列头部值是最大。
         return $this->singleQueue->bottom();
     }

}

Problem: 347. 前 K 个高频元素

关于php优先级队列《SplPriorityQueue》介绍

!!!以下内容为PHP手册优先级队列《SplPriorityQueue》的一些方法翻译!!!

public const int EXTR_BOTH; //与setExtractFlags搭配提取优先级和值
public const int EXTR_PRIORITY; //与setExtractFlags搭配只提取优先级
public const int EXTR_DATA; //与setExtractFlags搭配只提取值

SplPriorityQueue::compare -比较优先级，以便在筛选时将元素正确地放置在堆中
SplPriorityQueue::count -对队列中的元素数量进行计数
SplPriorityQueue::current -返回迭代器指向的当前节点
SplPriorityQueue::extract -从堆的顶部提取节点并向上筛选
SplPriorityQueue::getExtractFlags—获取提取的标志
SplPriorityQueue::insert—通过筛选将元素插入队列中
SplPriorityQueue:: iscorrupt -告知优先级队列是否处于损坏状态
SplPriorityQueue::isEmpty -检查队列是否为空
SplPriorityQueue::key -返回当前节点索引
SplPriorityQueue::next -移动到下一个节点
SplPriorityQueue::recoverFromCorruption -从损坏状态恢复并允许对队列进行进一步操作
SplPriorityQueue::rewind -将迭代器倒回开始(no-op)
SplPriorityQueue::setExtractFlags—设置提取模式
SplPriorityQueue::top -从队列的顶部查看节点
SplPriorityQueue::valid—检查队列中是否有更多节点

--详细可以转至手册地址：https://www.php.net/manual/zh/class.splpriorityqueue.php
--详细使用例程地址：http://www.noobyard.com/article/p-dvwxrekz-kg.html#google_vignette

需要注意的地方

php中《SplPriorityQueue》默认是使用高优先级优先。根据需要修改优先级。

class CustomedSplPriorityQueue extends SplPriorityQueue
{
 public function compare($priority1, $priority2): int
 {
     // return $priority1 - $priority2;//高优先级优先
     return $priority2 - $priority1;//低优先级优先
 }
}

根据题目设置提取模式。

setExtractFlags(EXTR_BOTH);//值和优先级都返回
setExtractFlags(EXTR_PRIORITY); //只返回优先级
setExtractFlags(EXTR_DATA); //只返回值

解题方法

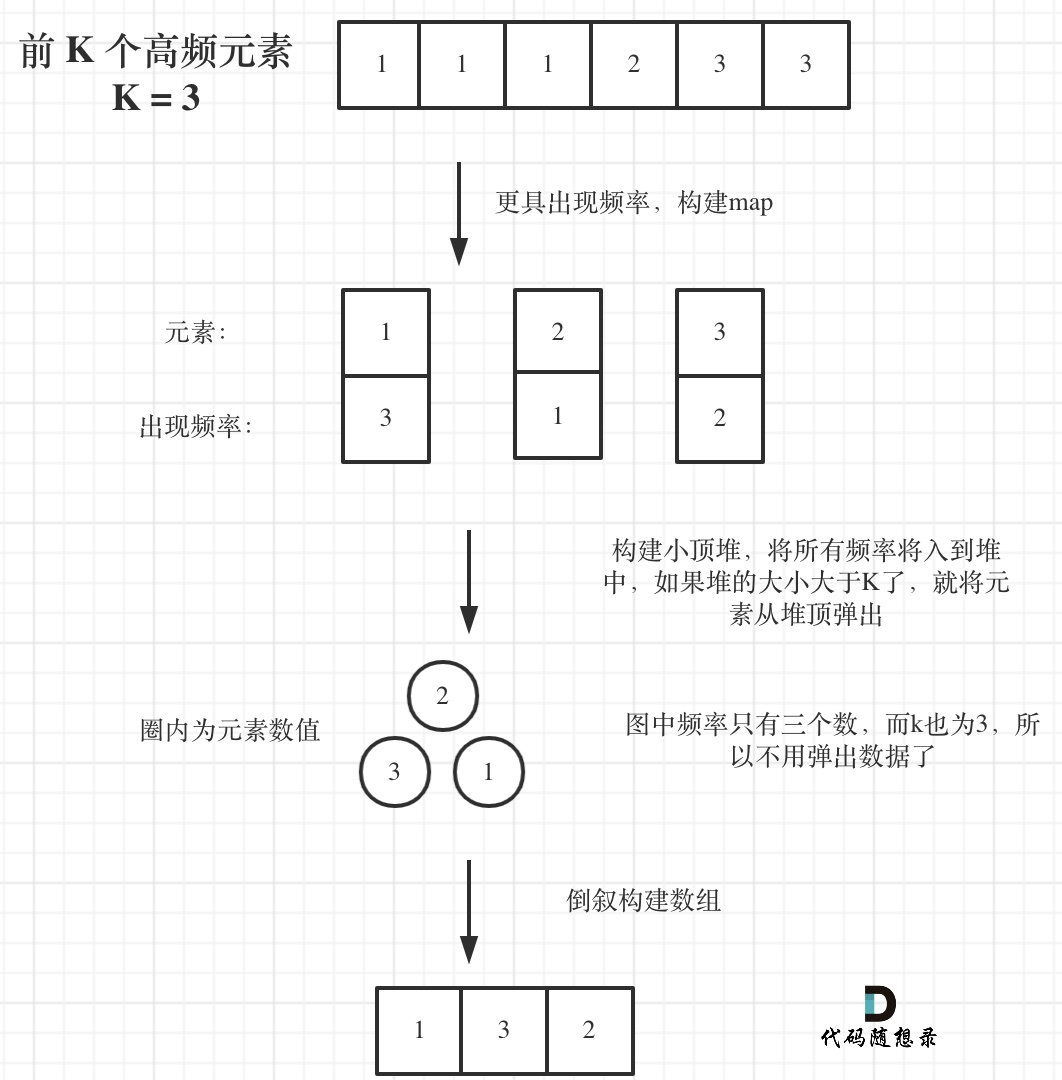
遍历目标数组，把每个元素与出现的次数记录为map数组。key为目标数组的值，val为出现的次数。
遍历map数组,使用优先级队列，设置低优先级优先（小顶堆），使出现频率高的值沉底。其次维持优先级队列长度为k。当超过长度k时，弹出顶部元素，即出现频率低的元素。直到遍历完成。剩余的k个元素即是出现频率最高的k个元素。
也可以使用高优先级解题（大顶堆），把所有map数组入队列。最后取顶端的k个元素即可。

复杂度

时间复杂度:

O(nlogk)

空间复杂度:

O(n)

小顶堆解法

class Solution {

    /**
     * @param Integer[] $nums
     * @param Integer $k
     * @return Integer[]
     */
    function topKFrequent($nums, $k) {
        $hashMap = [];
        foreach($nums as $key => $val){
            $hashMap[$val]++;
        }
        $splPriorityQueue = new \CustomedSplPriorityQueue();
        //public const int EXTR_BOTH; 值和优先级都返回
        //public const int EXTR_PRIORITY; 只返回优先级
        //public const int EXTR_DATA; 只返回值
        $splPriorityQueue->setExtractFlags(SplPriorityQueue::EXTR_DATA);
        foreach($hashMap as $key => $val){
            //插入优先级队列
            $splPriorityQueue->insert($key, $val);
            //保持优先级队列为k大小
            if($splPriorityQueue->count() > $k){
                $splPriorityQueue->extract();
            }
        }
        $res = [];
        while(!$splPriorityQueue->isEmpty()){
            $res[] = $splPriorityQueue->extract();
        }
        return $res;
    }
}

class CustomedSplPriorityQueue extends SplPriorityQueue
{
    //SplPriorityQueue默认是高优先级优先，重写为低优先级优先
    //当设置为低优先级优先数据结构为小顶堆，小顶堆的实质是二叉树，小的数在二叉树顶，
    //当优先级队列extract()/pop()元素时，会从堆顶开始弹出，保持堆为k大小，则最后留下的就是最大的k个数
    public function compare($priority1, $priority2): int
    {
        // return $priority1 - $priority2;//高优先级优先
        return $priority2 - $priority1;//低优先级优先
    }
}

大顶堆解法

class Solution {

    /**
     * @param Integer[] $nums
     * @param Integer $k
     * @return Integer[]
     */
    function topKFrequent($nums, $k) {
        $hashMap = [];
        //构建map数组
        foreach($nums as $key => $val){
            $hashMap[$val]++;
        }
        $splPriorityQueue = new SplPriorityQueue();
        //根据高优先级入队列
        foreach($hashMap as $key=>$val) {
            $splPriorityQueue->insert($key,$val);
        }
        $res = [];
        //取前k个值
        for($i = 0; $i < $k; $i++) {
            $res[] = $splPriorityQueue->extract();
        }
        return $res;
    }
}