739. 每日温度

单调栈基础概念

• 单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是整个数组只需要遍历一次。
  更直白来说，就是用一个栈来记录我们遍历过的元素，因为我们遍历数组的时候，我们不知道之前都遍历了哪些元素，以至于遍历一个元素找不到是不是之前遍历过一个更小的，所以我们需要用一个容器（这里用单调栈）来记录我们遍历过的元素。
• 通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了。时间复杂度为O(n)。例如:本题就是找到一个元素右边第一个比自己大的元素，此时就应该想到用单调栈了。
• 使用单调栈主要有三个判断条件。
  • 当前遍历的元素T[i] 小于 栈顶元素T[st.top()]的情况
  • 当前遍历的元素T[i] 等于 栈顶元素T[st.top()]的情况
  • 当前遍历的元素T[i] 大于 栈顶元素T[st.top()]的情况
• 这里我们要使用递增循序（再强调一下是指从栈头到栈底的顺序），因为只有递增的时候，栈里要加入一个元素i的时候，才知道栈顶元素在数组中右面第一个比栈顶元素大的元素是i。
  即：如果求一个元素右边第一个更大元素，单调栈就是递增的，如果求一个元素右边第一个更小元素，单调栈就是递减的。

解题方法

本题就是找到一个元素右边第一个比自己大的元素，此时就应该想到用递增单调栈了。
注意：栈中存入的元素时下标

1. 初始化res结果数组为0；
2. 把数组中的下标0入栈，从下标1的元素开始遍历，并且与栈顶元素做比较，如果遍历的元素T[i] <= 栈顶元素T[st.top()],则把当前遍历元素T[i]的下标i入栈，如果遍历的元素T[i] 大于 栈顶元素T[st.top()]，则使用while循环持续判断，收集当前下标差值，并且弹出当前元素，继续判断下一个新栈顶的值。while循环收集完结果后，将当前的for循环遍历的元素T[i]的下标入栈。

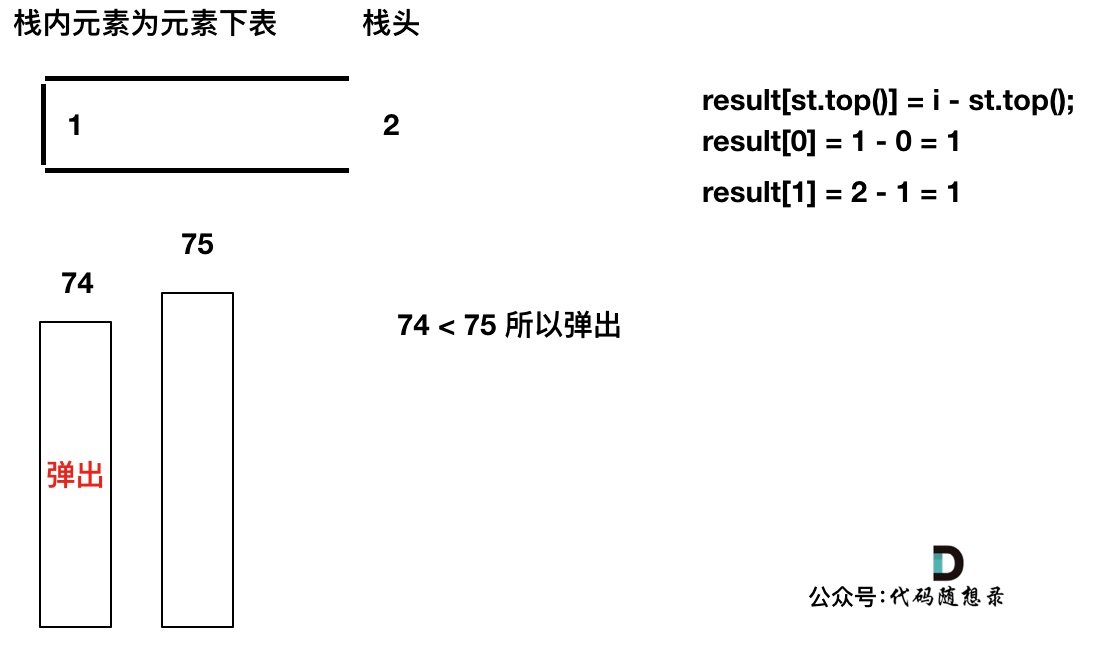
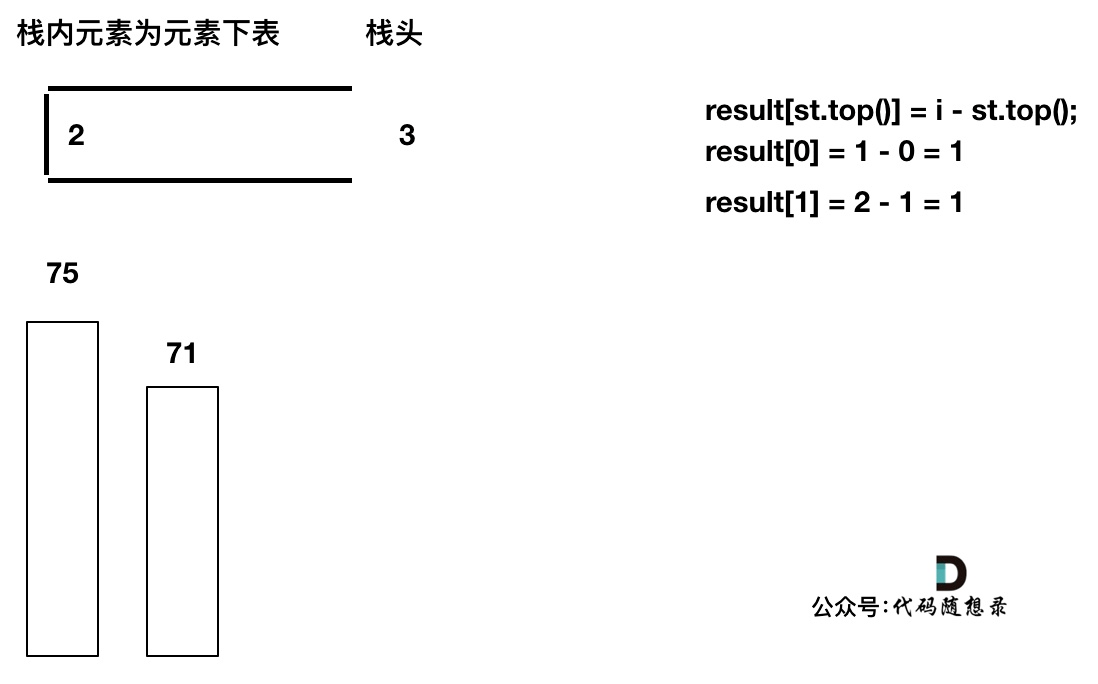
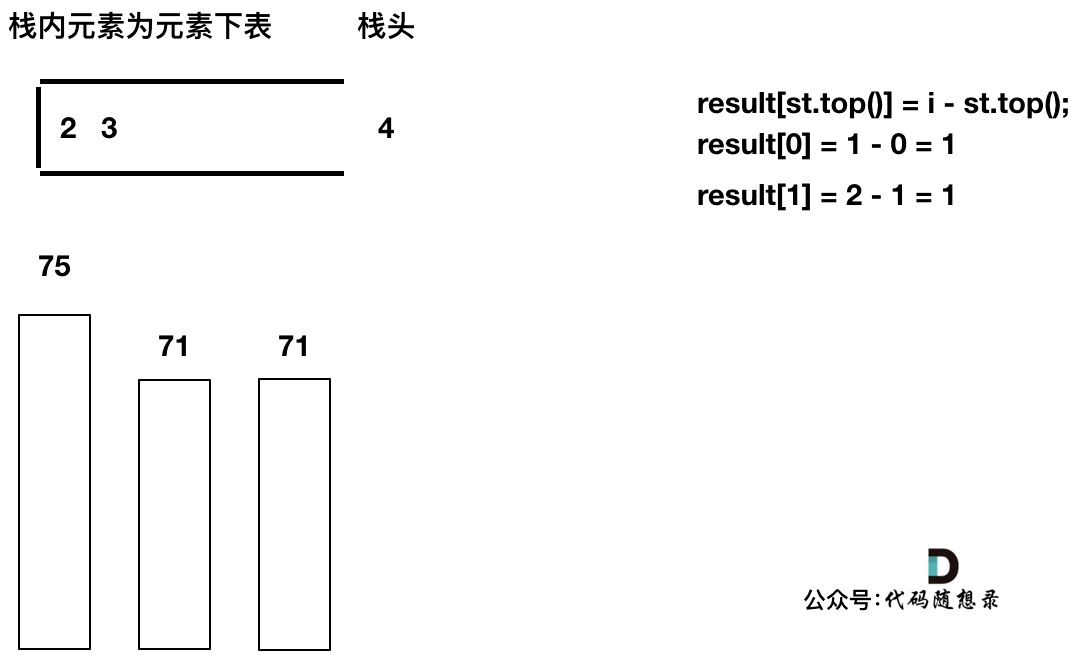
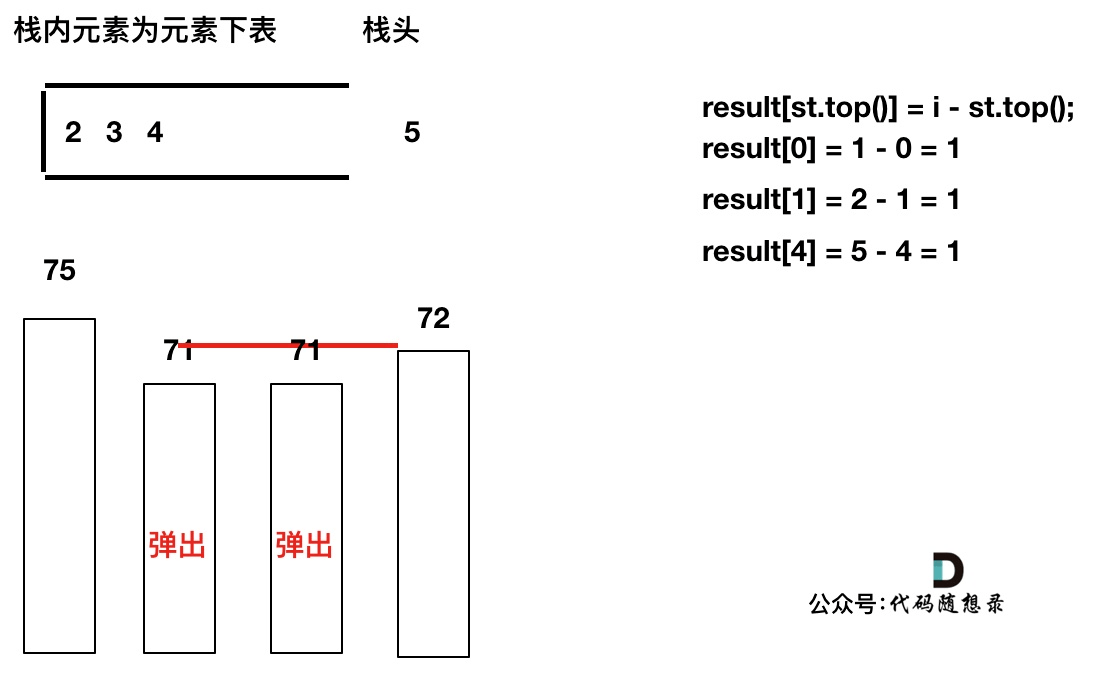
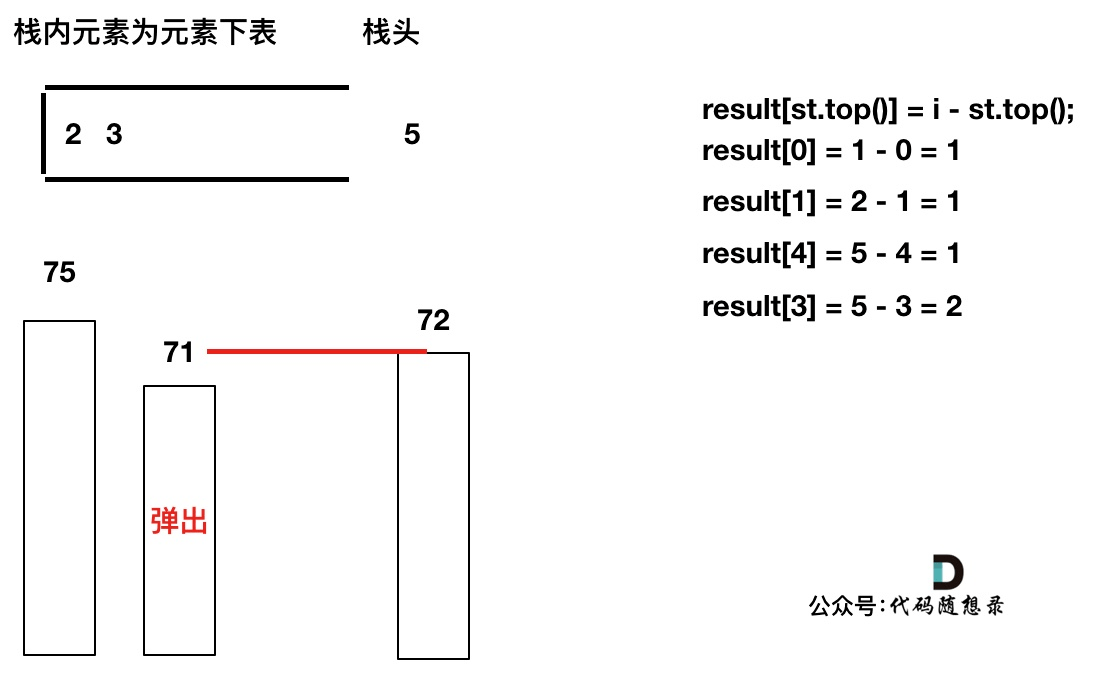
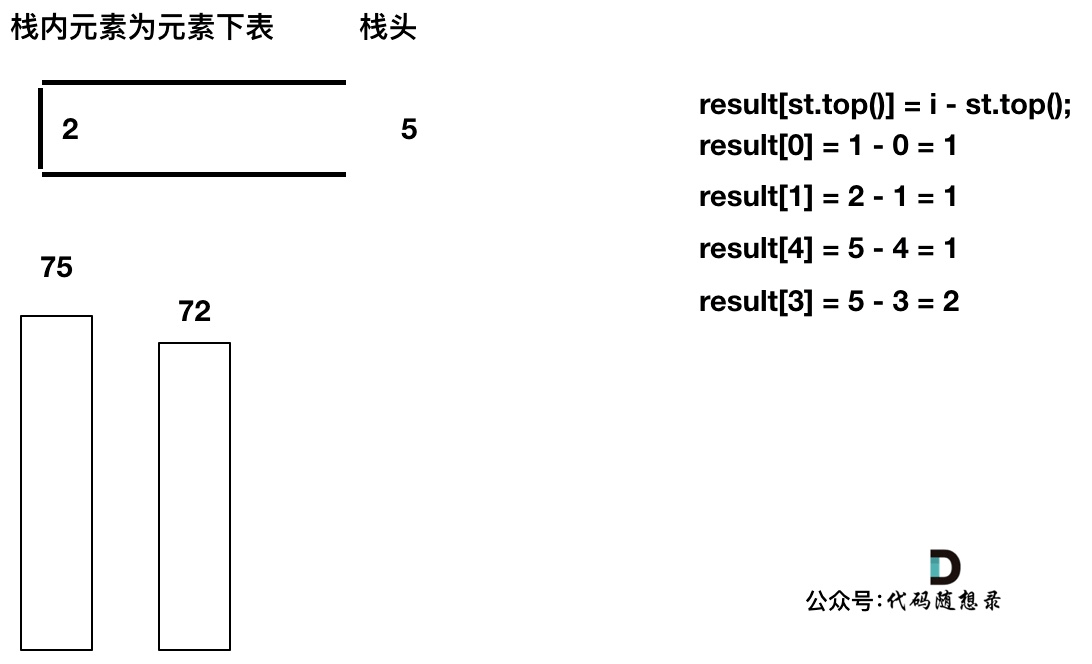
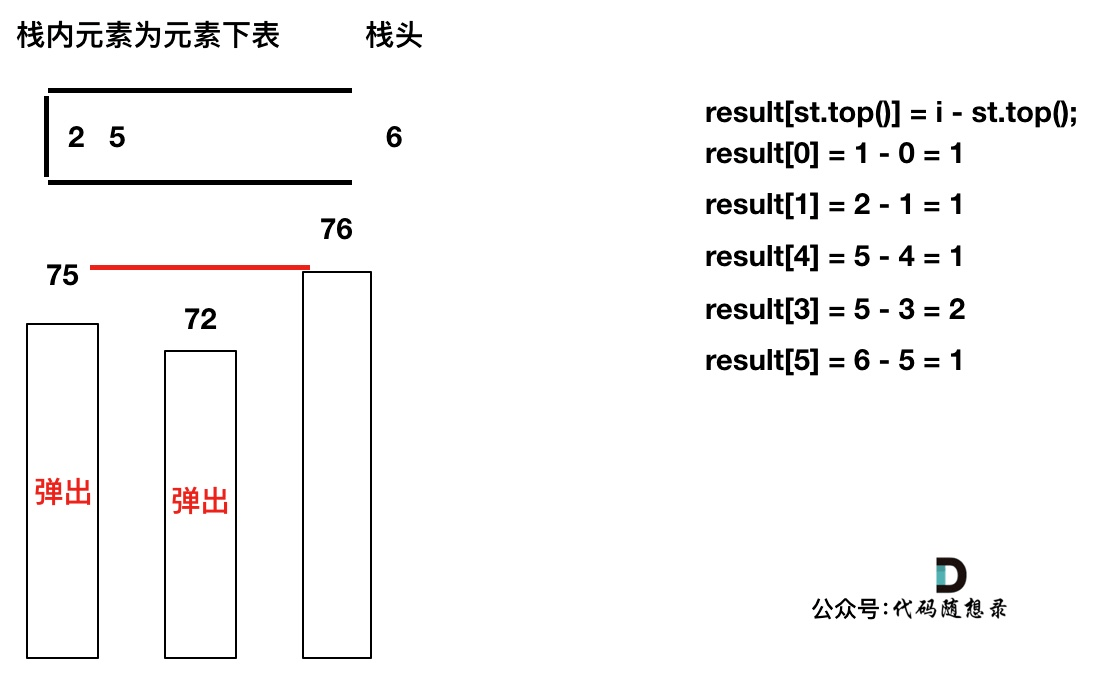
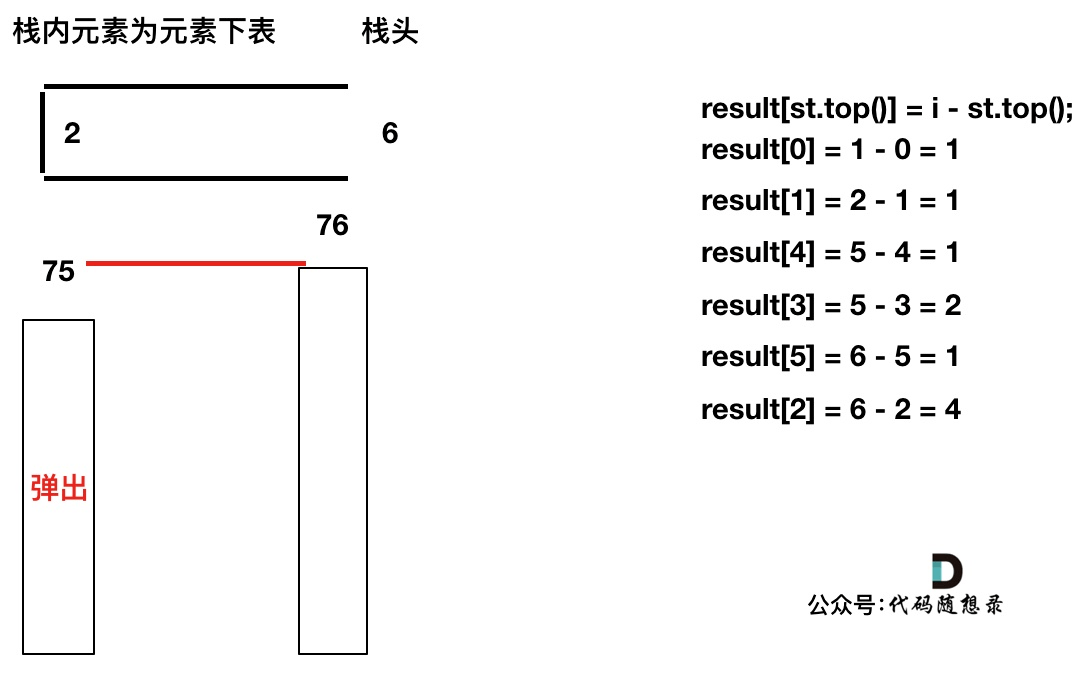
单调栈比较后出入栈的过程

以temperatures = [73, 74, 75, 71, 71, 72, 76, 73]为例来逐步分析，输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

tips: result[6] , result[7]怎么没更新啊，元素也一直在栈里。
其实定义result数组的时候，就应该直接初始化为0，如果result没有更新，说明这个元素右面没有更大的了，也就是为0。

code

单调栈解法

class Solution {

    /**
     * @param Integer[] $temperatures
     * @return Integer[]
     */
    function dailyTemperatures($temperatures) {
        $st = new SplStack();
        $len = count($temperatures);
        $res = array_fill(0, $len, 0);
        $st->push(0);//栈存的是索引
        for($i = 1; $i < $len; $i++){
            $top = $st->top();//取栈顶元素
            //$temperatures[$i]小于等于栈顶元素则入栈索引
            if($temperatures[$i] <= $temperatures[$top]){
                $st->push($i);
            }else{
                //$temperatures[$i] > 栈顶元素  则持续弹出并计算下标相减结果
                while(!$st->isEmpty() && $temperatures[$i] > $temperatures[$st->top()]){
                    $res[$st->top()] = $i - $st->top();
                    $st->pop();
                }
                //入栈索引
                $st->push($i);
            }
        }
        return $res;
    }
}

复杂度

时间复杂度

O(n)

空间复杂度

O(n)

暴力解法（超时）

class Solution {

    /**
     * @param Integer[] $temperatures
     * @return Integer[]
     */
    function dailyTemperatures($temperatures) {
        $arr = [];
        for($i = 0; $i < count($temperatures); $i++){
            $k = $i + 1;
            $mark = 0;
            while($k < count($temperatures)){
                if($temperatures[$k] > $temperatures[$i]){
                    $mark = 1;
                    break;
                }
                $k++;
            }
            $arr[] = $mark > 0 ? $k-$i : 0;
        }
        return $arr;
    }
}

复杂度

时间复杂度

O(n^2)

空间复杂度

O(1)

496. 下一个更大元素 I

解题方法

1. 本题可以沿用每日温度的单调栈逻辑，题目中说明了给你两个没有重复元素的数组num1,num2,其中nums1 是 nums2 的子集。需要求得下一个更大元素,
2. 那么可以使用每日温度的单调栈逻辑，求nums2中的所有下一个更大元素，每获取到一个时，判断当前遍历元素是否在nums1中，如果存在，则收集结果。

code

单调栈解法

class Solution {

    /**
     * @param Integer[] $nums1
     * @param Integer[] $nums2
     * @return Integer[]
     */
    function nextGreaterElement($nums1, $nums2) {
        $len1 = count($nums1);
        $len2 = count($nums2);
        $res = array_fill(0, $len1, -1);
        $map = [];
        for($i = 0; $i < $len1; $i++){
            $map[$nums1[$i]] = $i;
        }
        $st = new SplStack();
        $st->push(0);//入栈nums2的下标
        for($i = 1; $i < $len2; $i++){
            if($nums2 <= $nums2[$st->top()]){
                $st->push($i);
            }else{
                while(!$st->isEmpty() && $nums2[$i] > $nums2[$st->top()]){
                    //判断nums2[$st->top()] 是否存在nums1中才收集结果
                    if(in_array($nums2[$st->top()], $nums1)){
                        //获取nums1中的下标（这里也可以不用map，用array_search($nums2[$st->top()],$nums1);也是一样的意思
                        $index = $map[$nums2[$st->top()]];
                        $res[$index] = $nums2[$i];
                    }
                    $st->pop();
                }
                $st->push($i);
            }
        }
        return $res;
    }
}

复杂度

时间复杂度

O(n + m) n，m分别为nums1与nums2的长度

空间复杂度

O(n + m)

暴力解法(居然比单调栈还快)

class Solution {

    /**
     * @param Integer[] $nums1
     * @param Integer[] $nums2
     * @return Integer[]
     */
    function nextGreaterElement($nums1, $nums2) {
        $len1 = count($nums1);
        $len2 = count($nums2);
        //初始化数组
        $res = array_fill(0, $len1, -1);
        for($i = 0; $i < $len1; $i++){
            //在nums1中 寻找val = nums1[i]的下标
            $key = array_search($nums1[$i],$nums2);
            //遍历nums2
            for($j = $key; $j < $len2; $j++){
                if($nums2[$j] > $nums1[$i]){
                    //找到比nums[i]大的则更新目标数组，跳出内存循环
                    $res[$i] = $nums2[$j];
                    break;
                }
            }
        }
        return $res;
    }
}

复杂度

时间复杂度

O(n * m) n，m分别为nums1与nums2的长度

空间复杂度

O(1)

503. 下一个更大元素 II

解题方法

解题方法与每日温度基本一致。区别在于，本题是类似环形数组的问题。所以每日温度+环形数组处理逻辑就可以解决本题了。

1. 使用拼接一个相同数组来模拟环形，例如数组A: [1,2,1],拼接一个相同的数组形成数组B:[1,2,1, 1,2,1]就可以模拟环形了。
2. 使用取模/求余的方式。循环过程中len保持两倍长度，但是取数组值时，对下标与count(nums)做取模/求余的操作，保证nums数组不会越界。例如数组nums = [1,2,1],当下标i = 4时： i = i % count(nums) = 4 % 3 = 1。

code

单调栈解法

class Solution {

    /**
     * @param Integer[] $nums
     * @return Integer[]
     */
    function nextGreaterElements($nums) {
        $len = count($nums);
        $res = array_fill(0, $len, -1);
        $stack = new SplStack();
        $stack->push(0);
        //循环长度*2模拟环形数组
        for($i = 1; $i < $len * 2; $i++){
            $top = $stack->top();
            //用$i % $len取模/求余的方式保证i不会超过下标范围
            if($nums[$i % $len] <= $nums[$top]){
                $stack->push($i % $len);
            }else{
                //print_r([$stack->top(), $nums[$stack->top()], $i % $len, $nums[$i % $len]]);
                while(!$stack->isEmpty() &&  $nums[$stack->top()] < $nums[$i % $len]){
                    $res[$stack->top()] = $nums[$i % $len];
                    $stack->pop();
                }
                $stack->push($i % $len);
            }
        }
        return $res;
    }
}

复杂度

时间复杂度

O(n)

空间复杂度

O(n)

暴力解法(应该是踩线飘过)

class Solution {

    /**
     * @param Integer[] $nums
     * @return Integer[]
     */
    function nextGreaterElements($nums) {
        $len = count($nums);
        $res = array_fill(0, $len, -1);
        //循环长度*2模拟环形数组
        for($i = 0; $i < $len * 2; $i++){
            $k = $i + 1;
            while($k < $len * 2){
                //用$i % $len取模/求余的方式保证i不会超过下标范围
                if($nums[$k % $len] > $nums[$i % $len]) {
                    $res[$i % $len] = $nums[$k % $len];
                    break;
                }
                $k++;
            }
        }
        return $res;
    }
}

复杂度

时间复杂度

O(n ^ 2)

空间复杂度

O(1)

本作品采用《CC 协议》，转载必须注明作者和本文链接