代码随想录算法训练营第四十九天(完结撒花) | leetcode:接雨水,柱状图中最大的矩形
42. 接雨水
解题方法
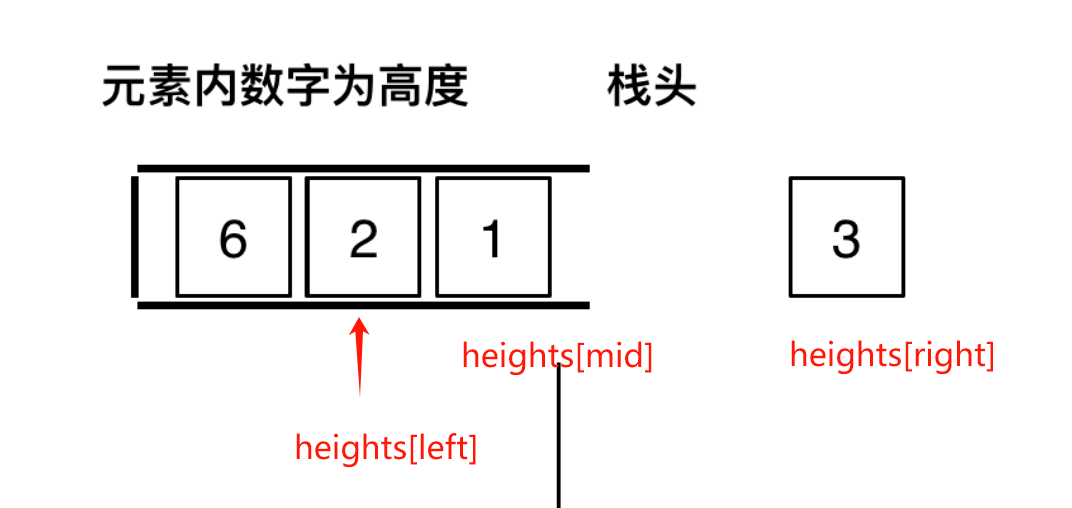
- 按图示可知:接雨水的条件是需要两边都要有比自己大的柱子才能装到雨水,即假设当前元素是height[i]时:需要求左边第一个比height[i]大的元素,以及右边第一个比height[i]大的元素。才能求得可以装下多少雨水。那么很明显是单调栈可以解决的问题。
- 使用递增单调栈,单调栈存入的是heights元素对应的下标。以栈顶元素为mid下标,栈顶元素的下一个元素为left下标,当前遍历元素为right下标。则可以得出:以mid为当前元素下标的话,heights[mid]左边第一个比自身大的元素是heights[left],右边第一个比自身大的元素是heights[right]
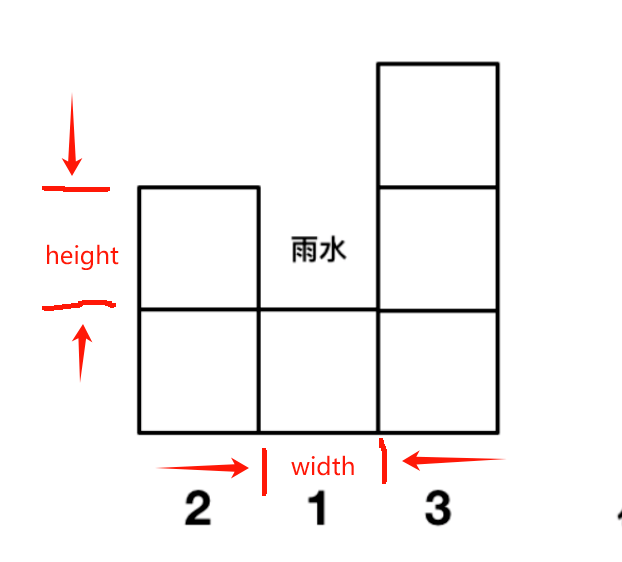
- 已知 mid , left , right 三个下标时,就可以开始求当前可以装雨水的数量了。根据木桶原理(盛水量由最低短板决定),盛水量高度height:由min(heights[left] , heights[right])- heights[mid] (减去底部的高度)决定。盛水量底板宽度width: 由right- left - 1(注意减一,只求中间宽度)可求得。则盛水量 = height * width。 假设下图下标从零开始,根据下图可得:盛水量 = (min(2,3) - 1) * (2 - 0 - 1) = 1。
- 最后遍历题目给定height数组,依次计算以每个元素为mid的情况,最后累加就得到整个数组可以装得的雨水量了。
code
单调栈解法
class Solution {
/**
* @param Integer[] $height
* @return Integer
*/
function trap($height) {
$len = count($height);
$sum = 0;
if($len <= 2) return $sum;
$st = new SplStack();
$st->push(0);//放入第一个下标
for($i = 1; $i < $len; $i++){
if($height[$i] < $height[$st->top()]){
//小于栈顶则入栈
$st->push($i);
}elseif($height[$i] == $height[$st->top()]){
$st->pop();//弹出重复元素
$st->push($i);//入栈
}else{
while(!$st->isEmpty() && $height[$i] > $height[$st->top()]){
$mid = $st->top();
$st->pop();//弹出后取左边最大值
if(!$st->isEmpty()){
$left = $st->top();
//左右大值取最小,然后减去mid底部高度,跟水桶短板一样原理
$h = min($height[$i], $height[$left]) - $height[$mid];
$w = $i - $left - 1;// 注意减一,只求中间宽度
$sum += $h * $w;//计算面积
}
}
$st->push($i);
}
}
return $sum;
}
}复杂度
时间复杂度
O(n)
空间复杂度
O(n)
84. 柱状图中最大的矩形
解题方法
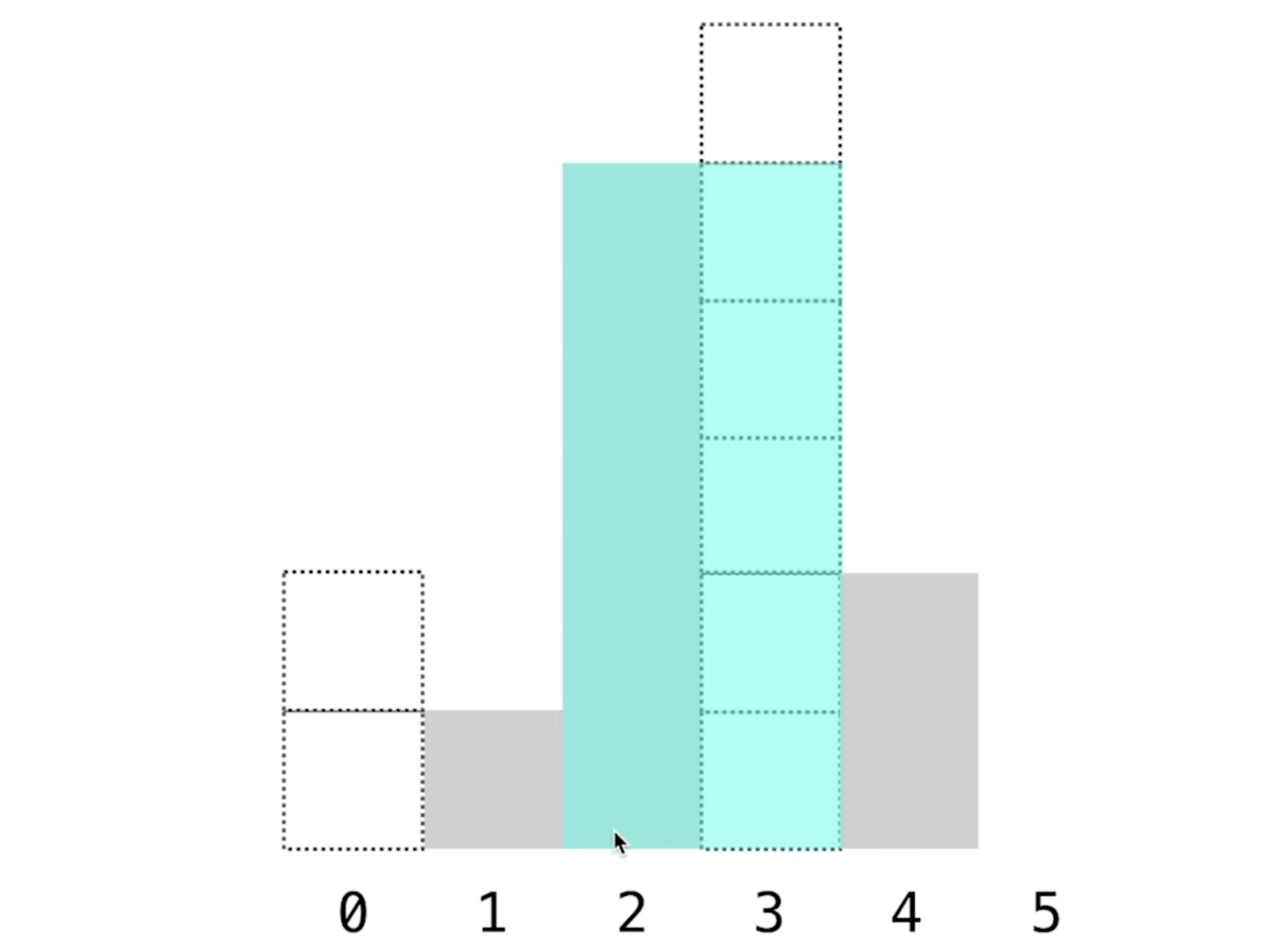
本题恰恰跟接雨水相反,接雨水需要求的当前元素左右两边第一个比自己大的元素,从而求得装雨水量。而本题则是需要求得当前元素左右两边第一个比自己小的元素,看看当前矩形可以扩散到哪里。如下图所示,假设当前元素为下标2的位置,则矩形最大只能扩散至蓝色部分。本题求比自己小的第一个元素, 那么使用单调递减栈。
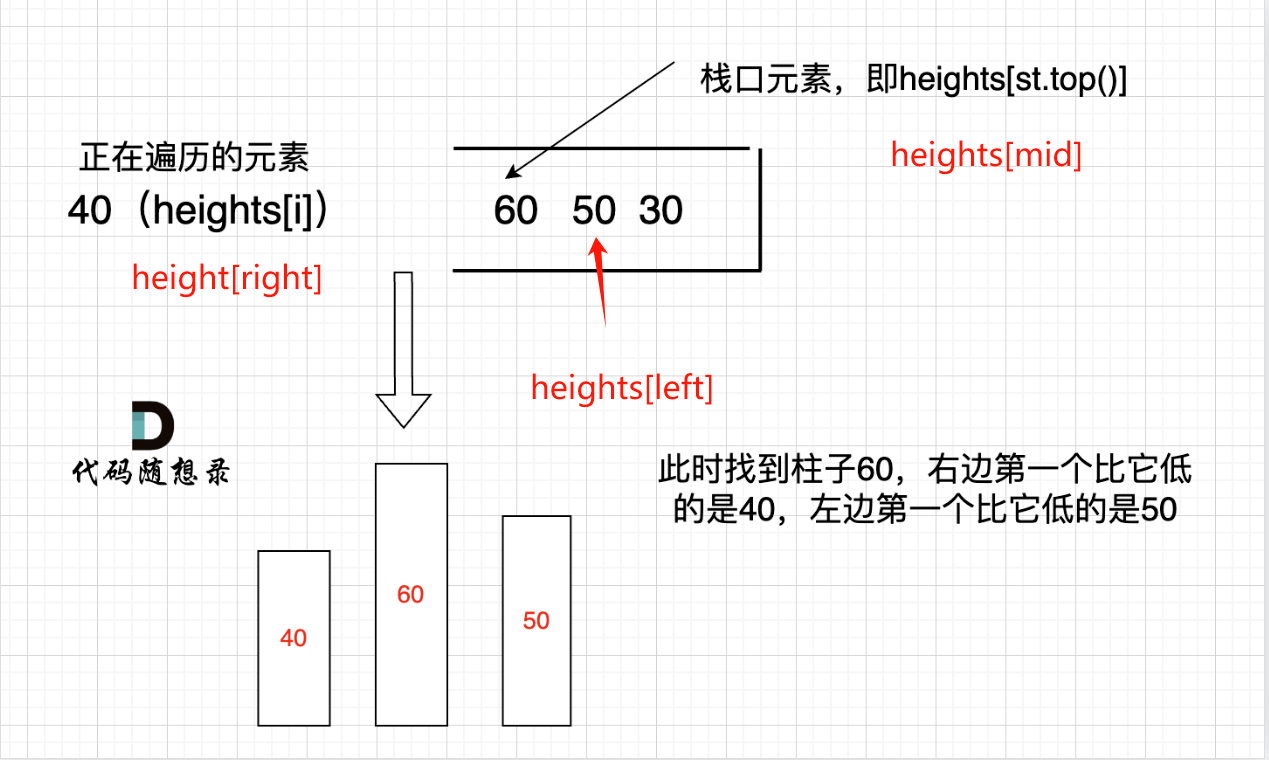
- 同样的,本题也需要求得mid, left, right三个元素才能求得以当前元素mid为中心的最大矩形。使用递减单调栈,单调栈存入的是heights元素对应的下标。以栈顶元素为mid下标,栈顶元素的下一个元素为left下标,当前遍历元素为right下标。则可以得出:以mid为当前元素下标的话,heights[mid]左边第一个比自身小的元素是heights[left],右边第一个比自身小的元素是heights[right]
- 已知mid, left, right三个下标,取矩形范围是左开又开的区间,即(left, right)宽度不能把left, right算上。所以当前元素heights[mid]是最小元素,也是柱状图中矩形的height,即height = heights[mid]。 柱状图中矩形的height可由right , left可得,即width = right - left - 1(注意减一,只求中间宽度)
- 本题最后需要求的是最大矩形,则遍历循环height数组元素,求得矩形面积与上次矩形面积比较,取最大值,以此类推,遍历结束后去的最大值。
需要注意的地方
遍历开始前需要在heights数组前后加入0。
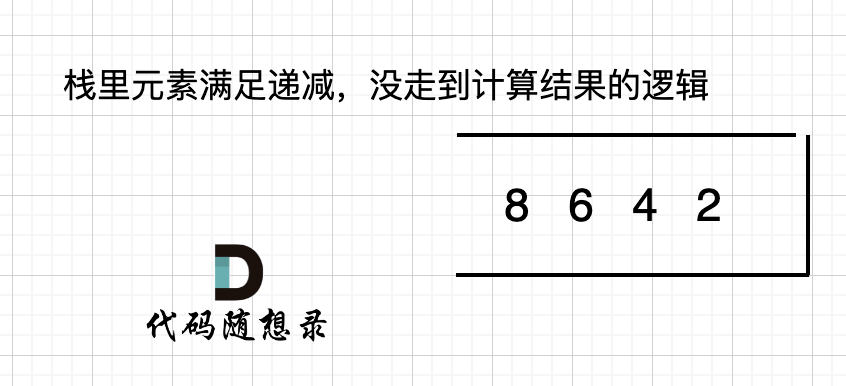
- 数组结尾加0的原因:假设数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,就会一直执行入栈操作,一直不会走计算结果的步骤,所以最后输出的就是0了。 (单调栈的模拟过程可以看上期的每日温度。)如图:
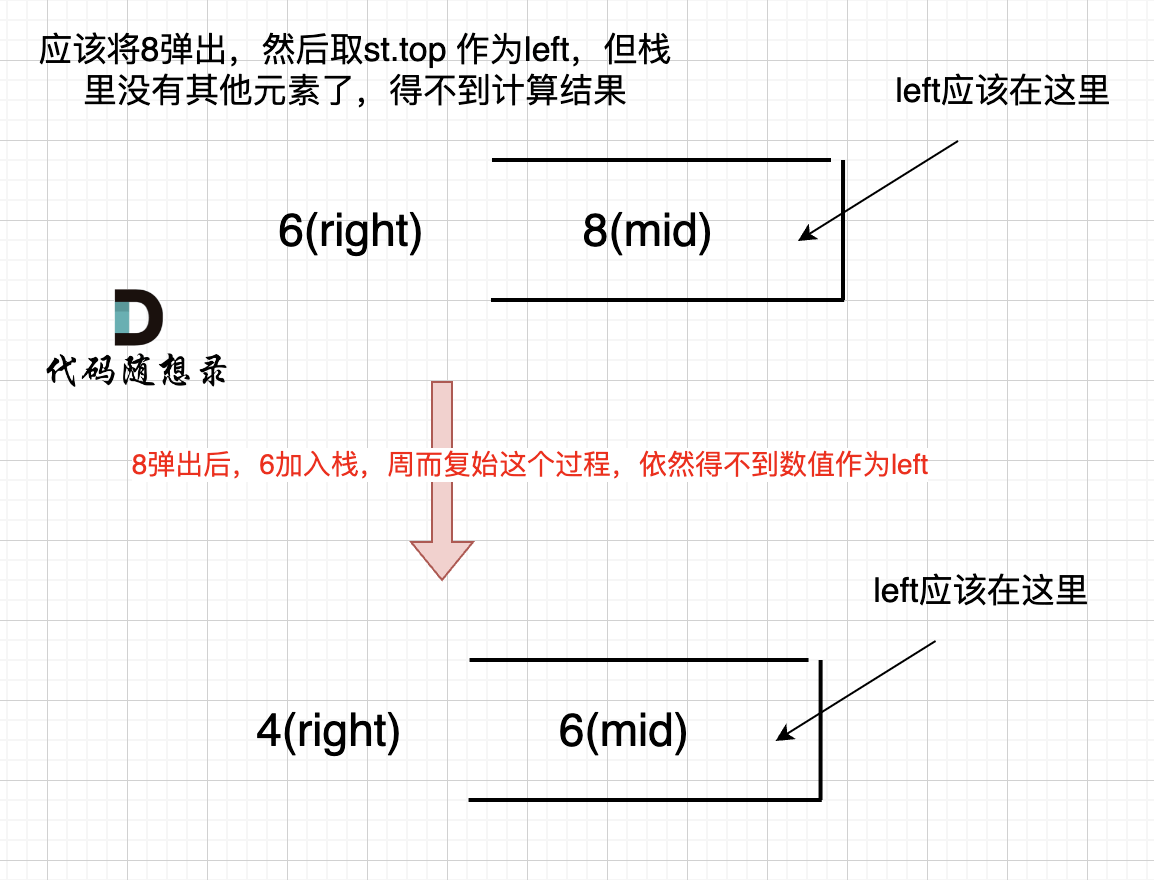
- 数组开头加0的原因::如果数组本身是降序的,例如 [8,6,4,2],在 8 入栈后,6 开始与8 进行比较,执行计算逻辑。此时我们得到 mid(8),rigt(6),但是得不到 left。所以需要加入一个0 <= heights[i] <= 10^4的最小值,作为初始left。
code
单调栈解法
class Solution {
/**
* @param Integer[] $heights
* @return Integer
*/
function largestRectangleArea($heights) {
$count = 0;
if($len == 1) return $heights[0];
//首尾加0 方便计算
array_unshift($heights,0);
array_push($heights,0);
$st = new SplStack();
$st->push(0);//第一个下标
$len = count($heights);
for($i = 1; $i < $len; $i++){
if($heights[$i] > $heights[$st->top()]){
$st->push($i);
}elseif($heights[$i] == $heights[$st->top()]){
$st->pop();//弹出相同元素去重
$st->push($i);
}else{
while(!$st->isEmpty() && $heights[$i] < $heights[$st->top()]){
$mid = $st->top();
$st->pop();//弹出栈顶,取左边比栈顶mid小的元素
if(!$st->isEmpty()){
$left = $st->top();//取左边比栈顶mid小的元素
$right = $i;//右边比栈顶mid小的元素
$h = $heights[$mid];
$w = $right - $left - 1;
$count = max($h*$w, $count);
}
}
$st->push($i);
}
}
return $count;
}
}复杂度
时间复杂度
O(n)
空间复杂度
O(n)
本作品采用《CC 协议》,转载必须注明作者和本文链接






 关于 LearnKu
关于 LearnKu



