代码随想录算法训练营第三十二天 | leetcode：不同路径,不同路径||
0 / 1 / 创建于 11个月前 /
_zzh 的个人博客
62. 不同路径
解题方法
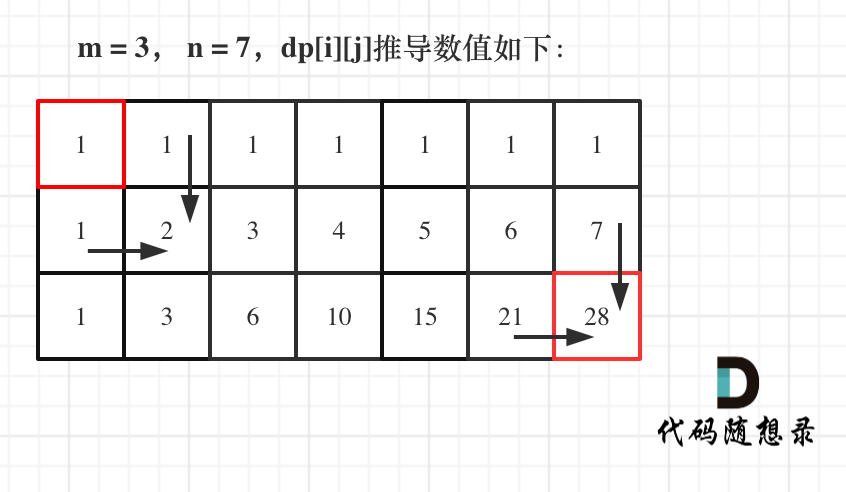
- dp[i][j] 表示走到[i,j]的位置有几种走法
- 当前位置[i,j]，因为机器人只能向下或者向右移动一步，所以要到达dp[i][j]，只能从它的上方到达或者它的左方到达。因为得出递推公式：dp[i][j] = dp[i-1][j] + dp[i][j-1];
- 因为机器人只能向下或者向右移动一步,所以当目的地在上边界或者下边界的时候到达的方式都只有一种。即：dp[0][j] = 1, dp[i][0] = 1;
- 因为需要由上方与左边的位置求得结果，所以遍历顺序为，从左到右，从上到下
code
动态规划常规解法
class Solution {
/**
* @param Integer $m
* @param Integer $n
* @return Integer
*/
function uniquePaths($m, $n) {
//初始化边界
for($i = 0; $i < $m; $i++){
$dp[$i][0] = 1;
}
for($j = 1; $j < $n; $j++){
$dp[0][$j] = 1;
}
//求解
for($i = 1; $i < $m; $i++){
for($j = 1; $j < $n; $j++){
$dp[$i][$j] = $dp[$i-1][$j] + $dp[$i][$j-1];
}
}
return $dp[$m-1][$n-1];
}
}复杂度
时间复杂度
O(m x n)
空间复杂度
O(m x n)
动态规划节省空间解法
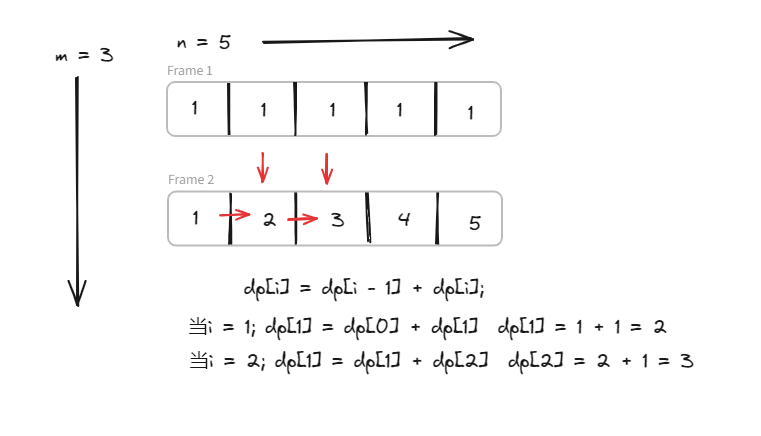
节省空间的原理就是，使用一个长度为n数组（x轴方向），不断的更新m次(y轴方向)。
当m = 1, i = 1; dp[1] = dp[0] + dp[1] dp[1] = 1 + 1 = 2。
当m = 1, i = 2; dp[1] = dp[1] + dp[2] dp[2] = 2 + 1 = 3。
辅助理解图
class Solution {
/**
* @param Integer $m
* @param Integer $n
* @return Integer
*/
function uniquePaths($m, $n) {
$dp = [];
//初始化x方向一维数组
for($i = 0; $i < $n; $i++) $dp[$i] = 1;
//先循环y方向，再循环x方向，不断更新一维数组的值
for($j = 1; $j < $m; $j++){
for($i = 1; $i < $n; $i++){
$dp[$i] = $dp[$i] + $dp[$i-1];
}
}
return $dp[$n-1];
}
}复杂度
时间复杂度
O(m x n)
空间复杂度
O(n)
Problem: 63. 不同路径 II
解题方法
解法和上一题大体相同，主要有以下几点不同
- 一定需要用新的dp数组并且默认值为0，不能直接操作原数组
- 处理障碍物的边界条件
- 初始化x,y边界时,需要判断障碍物在边界的情况
- 求解时，需要障碍物需要跳过，保持障碍物位置为0.
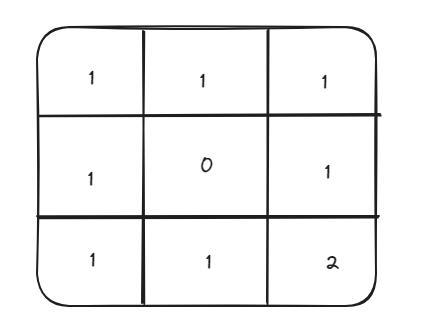
以 obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]为例子，最后打印的dp数组为。
code
动态规划常规解法
class Solution {
/**
* @param Integer[][] $obstacleGrid
* @return Integer
*/
function uniquePathsWithObstacles($obstacleGrid) {
$len1 = count($obstacleGrid);
$len2 = count($obstacleGrid[0]);
//当障碍物在左上角（起点）与右下角（终点）的情况，返回0，因为无法开始，无法到达
if($obstacleGrid[0][0] == 1 || $obstacleGrid[$len1-1][$len2-1] == 1) return 0;
//初始化db数组
for($i = 0; $i < $len1; $i++){
for($j = 0; $j < $len2; $j++){
$dp[$i][$j] = 0;
}
}
//初始化边界时需要判断障碍物不在当前边界时再初始化为1
for($i = 0; $i < $len1 && $obstacleGrid[$i][0] == 0; $i++) $dp[$i][0] = 1;
for($j = 0; $j < $len2 && $obstacleGrid[0][$j] == 0; $j++) $dp[0][$j] = 1;
for($i = 1; $i < $len1; $i++){
for($j = 1; $j < $len2; $j++){
//遇到障碍物需要跳过 障碍物 $dp[$i][$j] = 0；
if($obstacleGrid[$i][$j] == 1) continue;
$dp[$i][$j] = $dp[$i-1][$j] + $dp[$i][$j-1];
}
}
return $dp[$len1 - 1][$len2 - 1];
}
}复杂度
时间复杂度
O(m x n)
空间复杂度
O(m x n)
本作品采用《CC 协议》，转载必须注明作者和本文链接
关于 LearnKu
粤公网安备 44030502004330号
66