代码随想录算法训练营第四十七天 | leetcode：回文子串,最长回文子序列
0 / 0 / 创建于 10个月前 /
_zzh 的个人博客
647. 回文子串
解题方法
- dp数组的含义：dp[i][j]：表示从s[i]到s[j]这段字符串是否为回文子串 其中：i<=j
- 确定递推公式：主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同
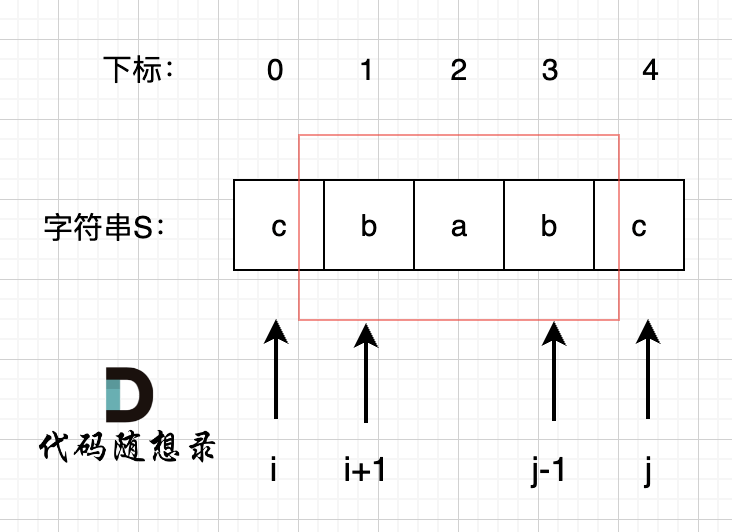
- if(s[i] == s[j])有三种情况：
- i == j: 指向同一个字符。即：if(i==j)dp[i][j] = true;
- j-i = 1: 此时为2个字符。即：if(j-i == 1)dp[i][j] = true;可以和上一种情况合并为:if(j-i <= 1)dp[i][j] = true;
- j-i > 1: 此时大于2个字符，因为对比顺序是从中间往两边扩散，需要从前一个字符，i+1,j-1推出，如果前一个字符相等，那么当前i,j也是回文子串。即:if（j-i > 1 && dp[i+1][j-1] == true）dp[i][j] = true
- 初始化dp数组：dp[i][j] = false。
- 遍历顺序：dp[i][j]依赖与[i+1][j-1]，所以遍历顺序外层从后往前，内层从前往后
code
动态规划解法1
class Solution {
/**
* @param String $s
* @return Integer
*/
function countSubstrings($s) {
$dp = [];
$len = strlen($s);
$res = 0;
for($i = $len-1; $i > 0; $i--){
for($j = $i; $j < $len; $j++){
$dp[$i][$j] = false;
}
}
for($i = $len-1; $i >= 0; $i--){
for($j = $i; $j < $len; $j++){
if($s[$i] == $s[$j]){
if($j-$i <= 1){
$dp[$i][$j] = true;
$res++;
}elseif($dp[$i+1][$j-1] == true){
$dp[$i][$j] = true;
$res++;
}
}
}
}
//print_r($dp);
return $res;
}
}复杂度
时间复杂度
O(n^2)
空间复杂度
O(n^2)
双指针解法
class Solution {
protected $num = 0;
protected $len = 0;
function countSubstrings($s) {
$this->len = strlen($s);
for ($i = 0; $i < $this->len; $i++) {
$this->getRes($s, $i, $i);// 以i为中心
$this->getRes($s, $i, $i+1);// 以i+1为中心
}
return $this->num;
}
protected function getRes($s, $left, $right) {
while($left >= 0 && $right <= $this->len && $s[$left] == $s[$right]) {
$this->num++;
$left--;
$right++;
}
}
}复杂度
时间复杂度
O(n^2)
空间复杂度
O(1)
516. 最长回文子序列
解题方法
- dp数组的含义：dp[i][j] ：字符串s在[i, j]范围内最长的回文子序列的长度
- 确定递推公式：
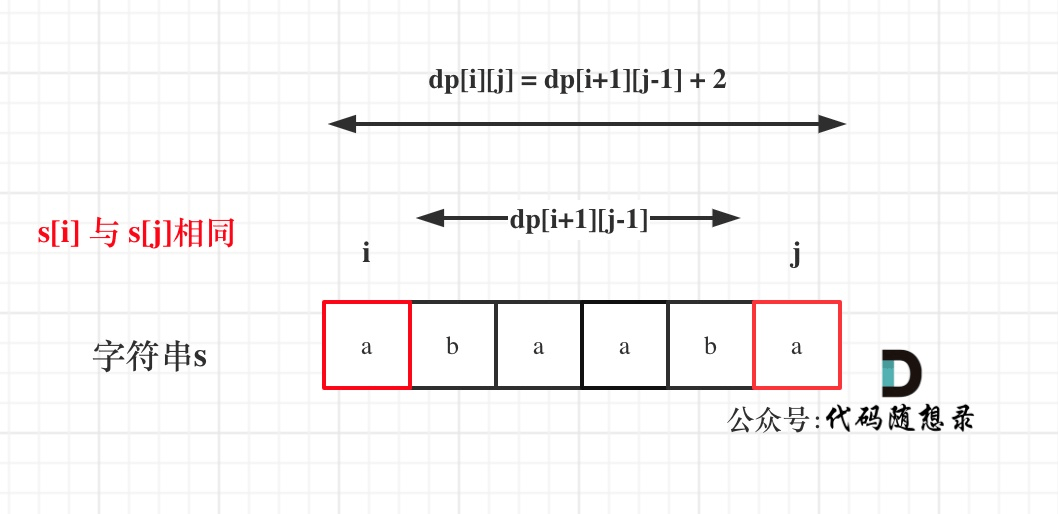
- if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1] + 2
如果遍历前一段字符为回文子串，那么当s[i] == s[j]时，那么这段字符串也是回文子串，所以当前遍历字符串的最长回文子序列长度就是在前端字符的最长回文子序列长度基础上+2。- if(s[i] != s[j]) dp[i][j] = min(dp[i+1][j],dp[i][j-1])
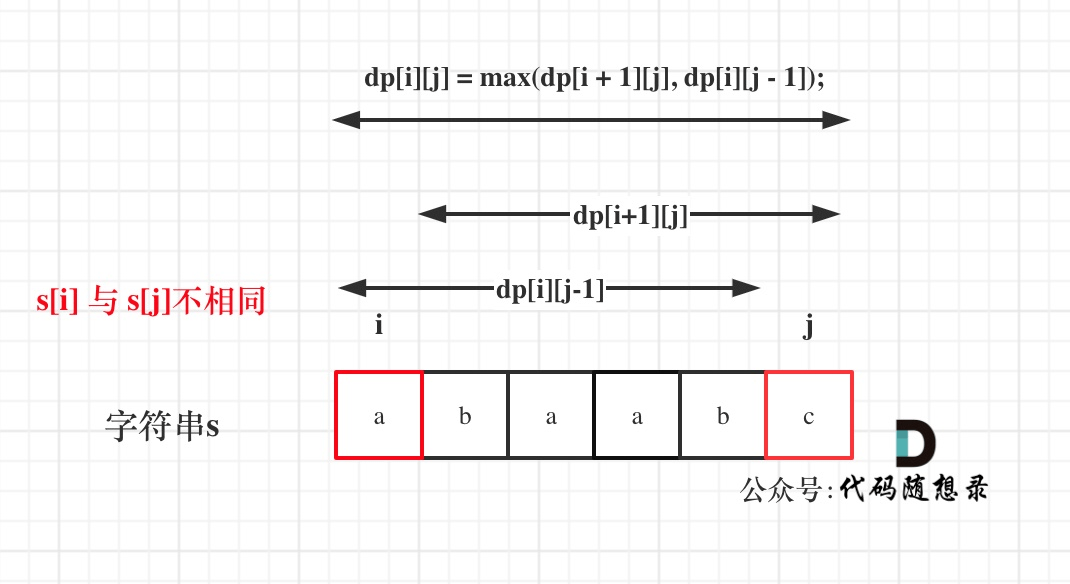
如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);- 初始化dp数组：当i=j时,初始化为1，即代指单个字符也是回文串的情况。其他初始化为0；
- 遍历顺序：dp[i][j]依赖与[i+1][j-1]，所以遍历顺序外层从后往前，内层从前往后
code
class Solution {
/**
* @param String $s
* @return Integer
*/
function longestPalindromeSubseq($s) {
$len = strlen($s);
if($len <= 1) return $len;
$dp = array_fill(0, $len, array_fill(0, $len, 0));
for($i = 0; $i < $len; $i++){
$dp[$i][$i] = 1;
}
for($i = $len - 1; $i >= 0; $i--){
for($j = $i + 1; $j < $len; $j++){
if($s[$i] == $s[$j]){
$dp[$i][$j] = $dp[$i+1][$j-1] + 2;
}else{
$dp[$i][$j] = max($dp[$i+1][$j], $dp[$i][$j-1]);
}
}
}
return $dp[0][$len-1];
}
}复杂度
时间复杂度
O(n^2)
空间复杂度
O(n^2)
本作品采用《CC 协议》，转载必须注明作者和本文链接
关于 LearnKu
粤公网安备 44030502004330号