代码随想录算法训练营第二天 | leetcode:有序数组的平方,长度最小的子数组 ,螺旋矩阵II
Problem: 977. 有序数组的平方
需要注意的问题
- 给定题目数组包含负数,负数平方为正数。需要注意平方后的排序。
- php解法需要初始化新数组键值位置,否则容易出现结果倒序输出的问题
解题方法
观察数据趋势,平方后从两边往中间是从大到小趋势。故而可以使用左右双指针方法,依次往中间移动,比较大小后,选择大的数插入新数组,并移动同向指针移动。直到循环结束完成排序。
复杂度
时间复杂度:
O(n)
空间复杂度:
O(n)
左闭右闭写法
function sortedSquares($nums) {
if(count($nums) <= 0){
return false;
}
$newArr = [];
$newIndex = count($nums)-1;
//需要初始化数组索引位置,不然输出结果为倒叙
for ($i = 0; $i < $newIndex; $i++) {
$newArr[$i] = 0;
}
$left = 0;
$right = count($nums)-1;
//双指针相向而行
while($left <= $right){
$leftDub = pow($nums[$left] , 2);
$rightDub = pow($nums[$right] , 2);
//如果左边比右边大 则把左边的值移入新数组 $newIndex-- $left++;
if($leftDub > $rightDub){
$newArr[$newIndex--] = $leftDub;
$left++;
}else{
//如果右边比左边大 则把右边的值移入新数组 $newIndex-- $right++;
$newArr[$newIndex--] = $rightDub;
$right--;
}
}
return $newArr;
}Problem: 209. 长度最小的子数组
需要注意的问题
- 需要考虑兼容数组所有数总和小于目标数的情况。如:target = 11。nums = [1,1,1,1,1,1,1,1];可以设置一个最大int常量数:PHP_INT_MAX,减少计算。
- 什么是滑动窗口:滑动窗口是双指针的一种特例,可以称为左右指针,在任意时刻,只有一个指针运动,而另一个保持静止。
- 需要考虑滑动窗口移动方式。如果用一个for循环,那么遍历指针应该表示滑动窗口的起始位置,还是终止位置。
解题方法
- 滑动窗口for循环遍历指针应该是对应滑动窗口的终止位置。
- 从0开始移动快指针寻找第一个大于target的目标区间,达到区间时(快指针不动),移动慢指针往快指针方向移动,寻找符合条件的更小区间。当慢指针移动时出现不满足大于target区间时,快指针继续移动,重复动作,更新最小区间值。直到遍历完成。
复杂度
时间复杂度:
O(n)
空间复杂度:
O(1)
Code
function minSubArrayLen($target, $nums) {
if (count($nums) <= 0) {
return 0;
}
$slow = 0;
$min = PHP_INT_MAX;//要用大于数组长度的值
//快指针先找到第一组比target大的数组长度
for($fast = 0; $fast <= count($nums)-1; $fast++){
//计算快指针移动区间总和
$sum += $nums[$fast];
//找到之后移动慢指针逐渐缩小区间找到最小长度
while($sum >= $target){
//区间长度包含首尾是闭区间,需要+1
$len = $fast - $slow + 1;
$min = min($min,$len);
//注意更新sum值:慢指针往快指针移动一步,区间减小,sum需要减去区间外的值
$sum -= $nums[$slow];
$slow++;
}
}
//适配数组内没有符合长度的情况
return $min == PHP_INT_MAX ? 0 : $min;
}Problem: 59. 螺旋矩阵 II
需要注意的问题
- 循环矩阵四条边时,需要遵循统一的,循环不变量规则。即上期二分法中,左闭右闭与左闭右开。
- 一定一定要画一个矩阵的数组下标图,非常有助于理解循环过程的边界。
- 圈数为单数时,需要单独处理中心点。
解题方法
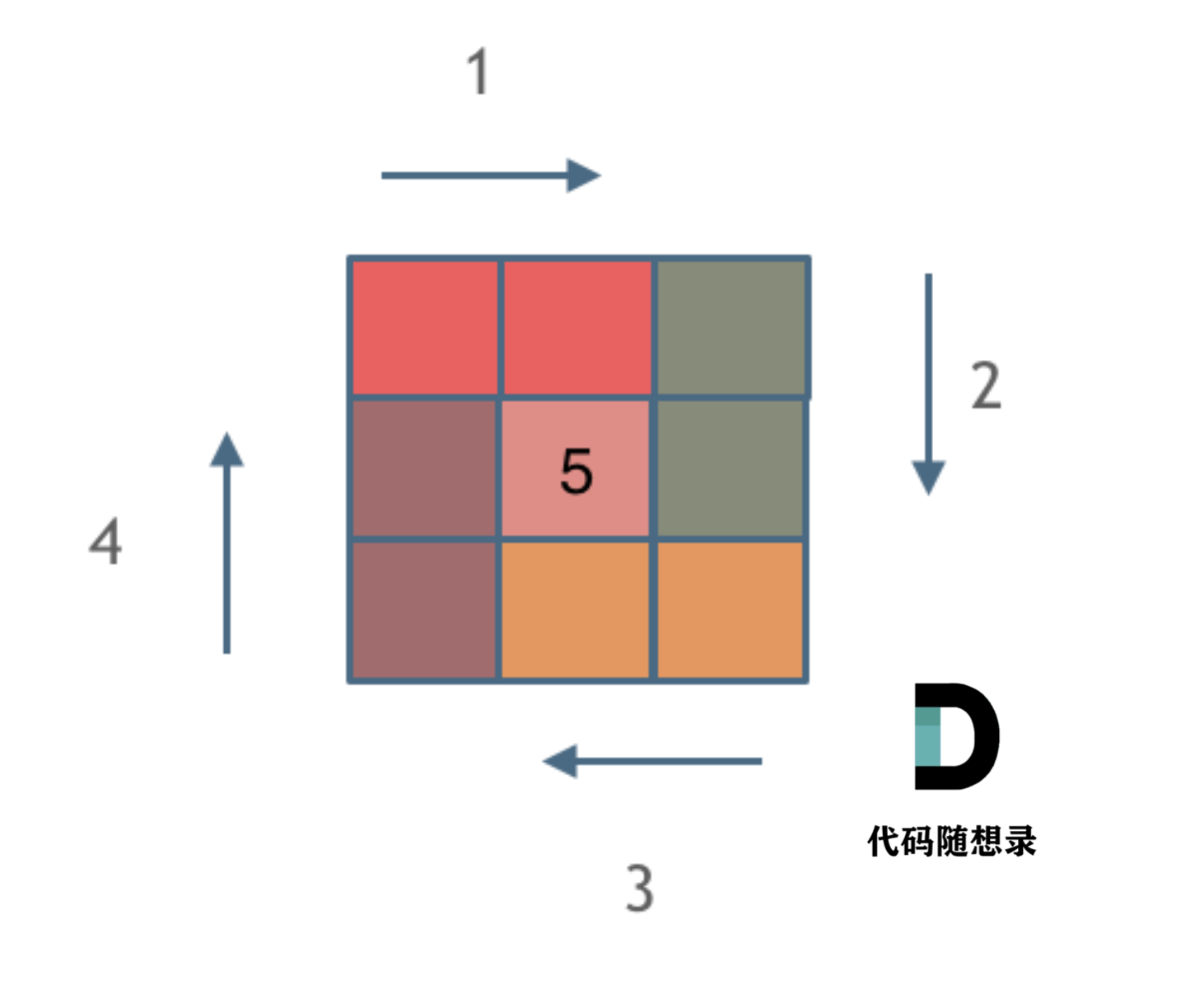
模拟顺时针画矩阵的过程,每一条边都要坚持一致的左闭右开:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
复杂度
时间复杂度:
O(n^2)
空间复杂度:
O(1)
关于为啥空间复杂度是O(1)。关于空间复杂度的定义(摘自百度百科):空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。
题目需要我们输出一个n x n的矩阵数组,所以,这里不算临时占用的空间。而解法中没有其余跟n成线性关系的空间开辟,所以空间复杂度为O(1);
Code
function generateMatrix($n) {
//使用循环不变量,左闭右开原则
$startX = 0;//起始X
$startY = 0;//起始Y
$res = [];//结果集
$count = 1;//计数
$offset = 1;//边界偏移量
$round = floor($n/2);//循环圈数
//初始化数组默认值
for($k = 0; $k < $n; $k++){
for($v = 0;$v < $n; $v++){
$res[$k][$v] = null;
}
}
while($round > 0){
//上边 (0,0) (0,1)
for($j = $startY; $j < ($n - $offset); $j++){
$res[$startX][$j] = $count++;
}
//右边 (0,2) (1,2)
for($i = $startX; $i < ($n - $offset); $i++){
$res[$i][$j] = $count++;
}
//下边 (2,2) (2,1)
for(; $j > $startY; $j--){
$res[$i][$j] = $count++;
}
//左边 (2,0) (1,0)
for(; $i > $startX; $i--){
$res[$i][$j] = $count++;
}
//X,Y +1改变起始位置,进入内圈
$startX++;
$startY++;
//内圈循环偏移量需要+1
$offset++;
//圈数--
$round--;
};
//处理单圈数中点
if($n%2 == 1){
$res[$startX][$startY] = $count;
}
return $res;
}本作品采用《CC 协议》,转载必须注明作者和本文链接









 关于 LearnKu
关于 LearnKu



