代码随想录算法训练营第三十九天 | leetcode:打家劫舍,打家劫舍II,打家劫舍III
198. 打家劫舍
解题方法
- dp数组的含义:dp[i]:当房屋数量为i时,能偷窃到的最高金额为dp[i];
- 确定递推公式:max(dp[i-1], dp[i-2] + nums[i]);;
- dp[i-1]表示不偷窃nums[i]
- dp[i-2] + nums[i]表示偷窃nums[i],i-2是因为不能偷窃相邻房屋,所以要偷窃nums[i],就不能算上nums[i-1]
- 初始化dp数组:dp[0] = nums[0],dp[1] = max(nums[0],nums[1]);
- 遍历顺序:从小到大。
code
class Solution {
/**
* @param Integer[] $nums
* @return Integer
*/
function rob($nums) {
$dp = [];
$len = count($nums);
//初始化dp数组
for($i = 0; $i < $len; $i++) $dp[$i] = 0;
$dp[0] = $nums[0];
$dp[1] = max($nums[0],$nums[1]);
//i从2开始
for($i = 2; $i < $len; $i++){
//从偷取房屋i与不偷取房屋i中取最大值
$dp[$i] = max($dp[$i-1], $dp[$i-2] + $nums[$i]);
}
return $dp[$len - 1];
}
}复杂度
时间复杂度
O(n),其中 n 为 nums 的长度
空间复杂度
O(n)
213. 打家劫舍 II
解题方法
思路:对于一个数组,成环的话主要有如下三种情况。
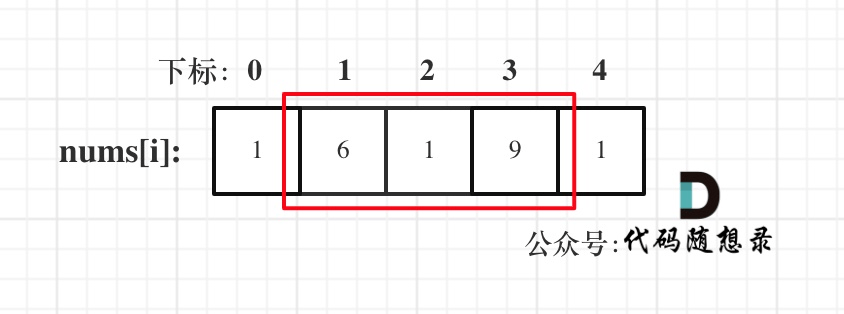
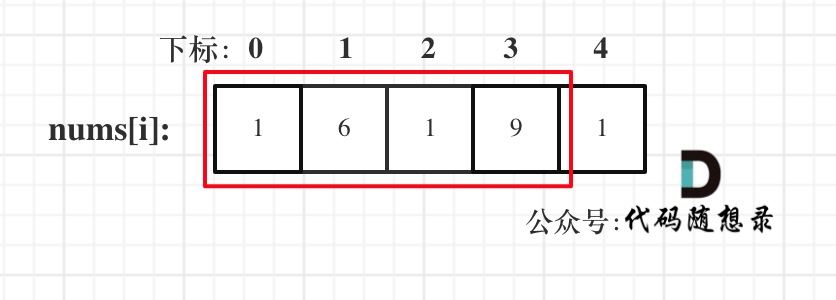
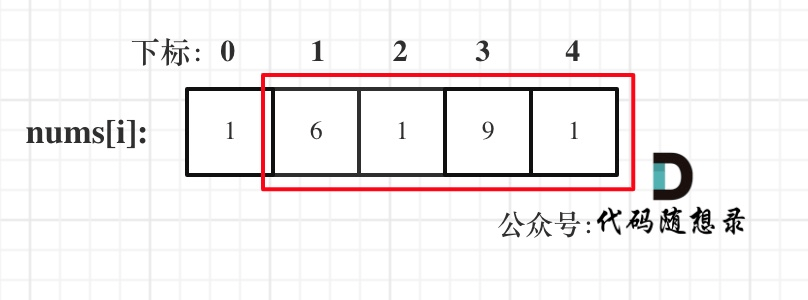
- 情况一:考虑不包含首尾元素
- 情况二:考虑包含首元素,不包含尾元素
- 情况三:考虑包含尾元素,不包含首元素
- !!!情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了!!!。
- 把情况二和情况三截取为线性数组,分别代入打家劫舍1,最后求最大值即可。
- dp数组的含义:dp[i]:当房屋数量为i时,能偷窃到的最高金额为dp[i];
- 确定递推公式:max(dp[i-1], dp[i-2] + nums[i]);;
- dp[i-1]表示不偷窃nums[i]
- dp[i-2] + nums[i]表示偷窃nums[i],i-2是因为不能偷窃相邻房屋,所以要偷窃nums[i],就不能算上nums[i-1]
- 初始化dp数组:dp[0] = nums[0],dp[1] = max(nums[0],nums[1]);
- 遍历顺序:从小到大。
code
class Solution {
/**
* @param Integer[] $nums
* @return Integer
*/
function rob($nums) {
/**
思路:把环形问题,抽象为两个先写数组,1.考虑头元素 2. 不考虑头元素,3.用打家劫舍1的解法,然后求1和2的最大值
*/
if (count($nums) == 0) return 0;
if (count($nums) == 1) return $nums[0];
$len = count($nums);
//截取情况三:考虑包含尾元素,不包含首元素
$nums1 = array_slice($nums, 1, $len);
//截取情况二:考虑包含首元素,不包含尾元素
$nums2 = array_slice($nums, 0, $len - 1);
//分别求解
$dp1 = $this->getDp($nums1);
$dp2 = $this->getDp($nums2);
//取最大值
return max($dp1,$dp2);
}
//打家劫舍1的逻辑
function getDp($nums){
$dp = [];
$len = count($nums);
//初始化dp数组
for($i = 0; $i < $len; $i++) $dp[$i] = 0;
$dp[0] = $nums[0];
$dp[1] = max($nums[0],$nums[1]);
//i从2开始
for($i = 2; $i < $len; $i++){
//从偷取房屋i与不偷取房屋i中取最大值
$dp[$i] = max($dp[$i-1], $dp[$i-2] + $nums[$i]);
}
return $dp[$len - 1];
}
}复杂度
时间复杂度
O(n)
空间复杂度
O(n)
337. 打家劫舍 III
解题方法
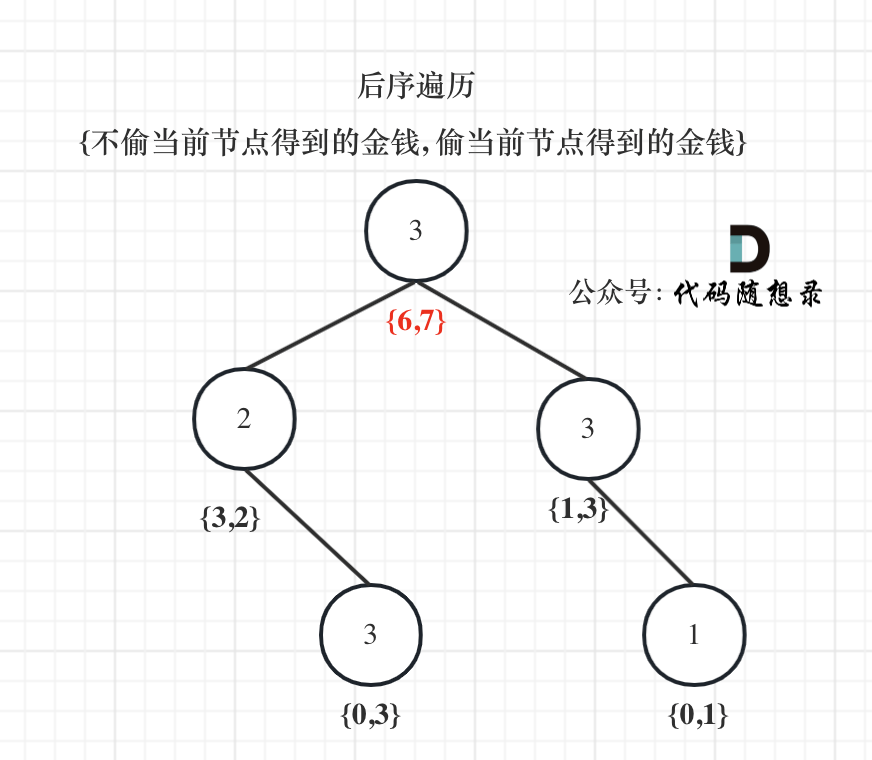
思路:利用后序遍历(左右中),自底向上传递dp数组:dp[0]表示不偷当前节点,dp[1]表示偷当前节点,不断更新偷当前节点值,和不偷当前节点值的状态。
- 当偷当前节点值时,dp[0]等于当前节点值;
- 当不偷当前节点时,就代表选择偷左右孩子节点。dp[1] = max(left[0], left[1]) + max(right[0], right[1]);
- dp数组的含义:使用长度为2的dp数组表示当前节点的状态,dp[0]表示不偷当前节点,dp[1]表示偷当前节点
- 确定递推公式:因为只有dp[0], dp[1],所以本题没有递推公式;
- 初始化dp数组:dp[0] = 0,dp[1] = 0;
- 遍历顺序:二叉树后序遍历。
code
class Solution {
private $dp;//定义dp数组
/**
* @param TreeNode $root
* @return Integer
*/
function rob($root) {
$this->dp[0] = 0;//不偷当前节点
$this->dp[1] = 0;//偷当前节点
$res = $this->treeLoop($root);
return max($res[0], $res[1]);
}
function treeLoop($node){
if($node == null) return [0,0];
//遍历左子树
$left = $this->treeLoop($node->left);
//遍历右子树
$right = $this->treeLoop($node->right);
//不偷当前节点:偷左孩子与不偷左孩子的最大值 + 偷右孩子与不偷右孩子的最大值
$notCur = max($left[0],$left[1]) + max($right[0],$right[1]);
//偷当前节点 $left[0]:不偷左孩子 $right[0]:不偷右孩子
$getCur = $node->val + $left[0] + $right[0];
return [$notCur,$getCur];
}
}复杂度
时间复杂度
O(n),其中 n 为 nums 的长度
空间复杂度
O(n)
本作品采用《CC 协议》,转载必须注明作者和本文链接




 关于 LearnKu
关于 LearnKu



