代码随想录算法训练营第二十五天 | leetcode:分发饼干 ,摆动序列,最大子数组和
455. 分发饼干
注意的地方
- 每个孩子最多只能给一块饼干。
- 目标是尽可能满足越多数量的孩子。
解题方法
先将数组从小到大排序,同时遍历孩子数组与饼干数组。以饼干数值最大值开始匹配符合条件的孩子,如果找到了那么同时跳过该饼干和孩子元素,进行新一轮的匹配,直到遍历完成。
复杂度
时间复杂度
O(nlogn)
空间复杂度
O(1)
code
class Solution {
/**
* @param Integer[] $g
* @param Integer[] $s
* @return Integer
*/
function findContentChildren($g, $s) {
$i = count($g) - 1;
$j = count($s) - 1;
$count = 0;
//排序方便从大到小遍历
sort($g);
sort($s);
while($i >= 0 && $j >= 0){
//print_r([$i,$j]);
//如果最大饼干分发出去则,孩子胃口数组与饼干尺寸数组下标都向左移动
if($s[$j] >= $g[$i]){
$i--;
$j--;
$count++;
}else{
//如果饼干没分发出去,则孩子往左移,匹配胃口更小的孩子
$i--;
}
}
return $count;
}
}376. 摆动序列
注意的地方
仅有一个元素或者含两个不等元素的序列也视作摆动序列。 也就是说一个元素最长子序列的长度为1,两个不等元素的序列的最长子序列的长度为2,重复元素视为一个长度。
所以题目中需要特别注意数组中含有重复元素的情况。
解题方法
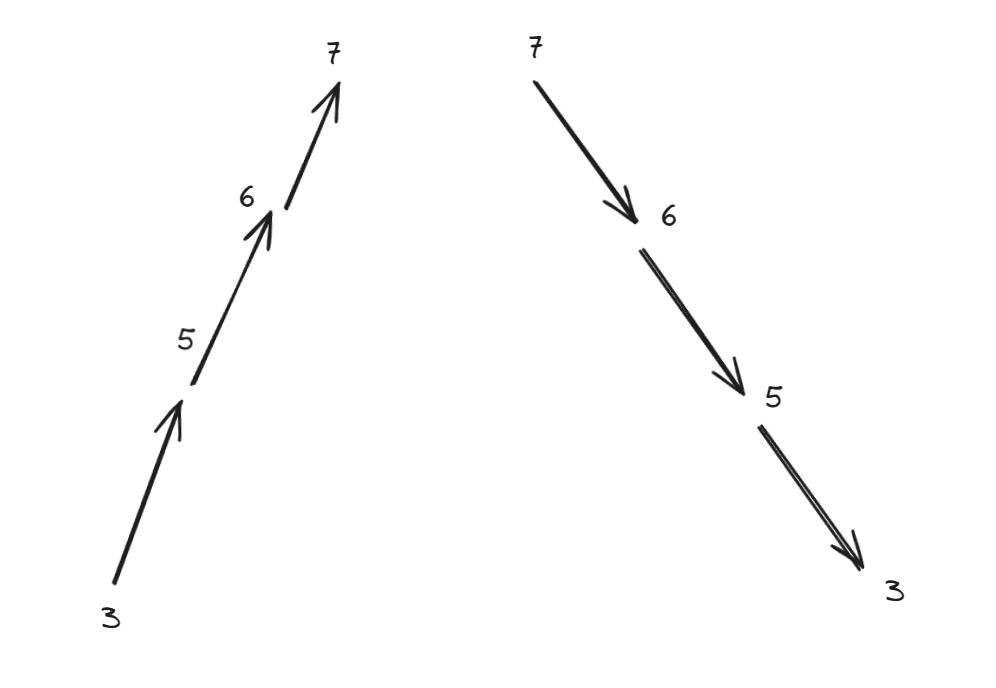
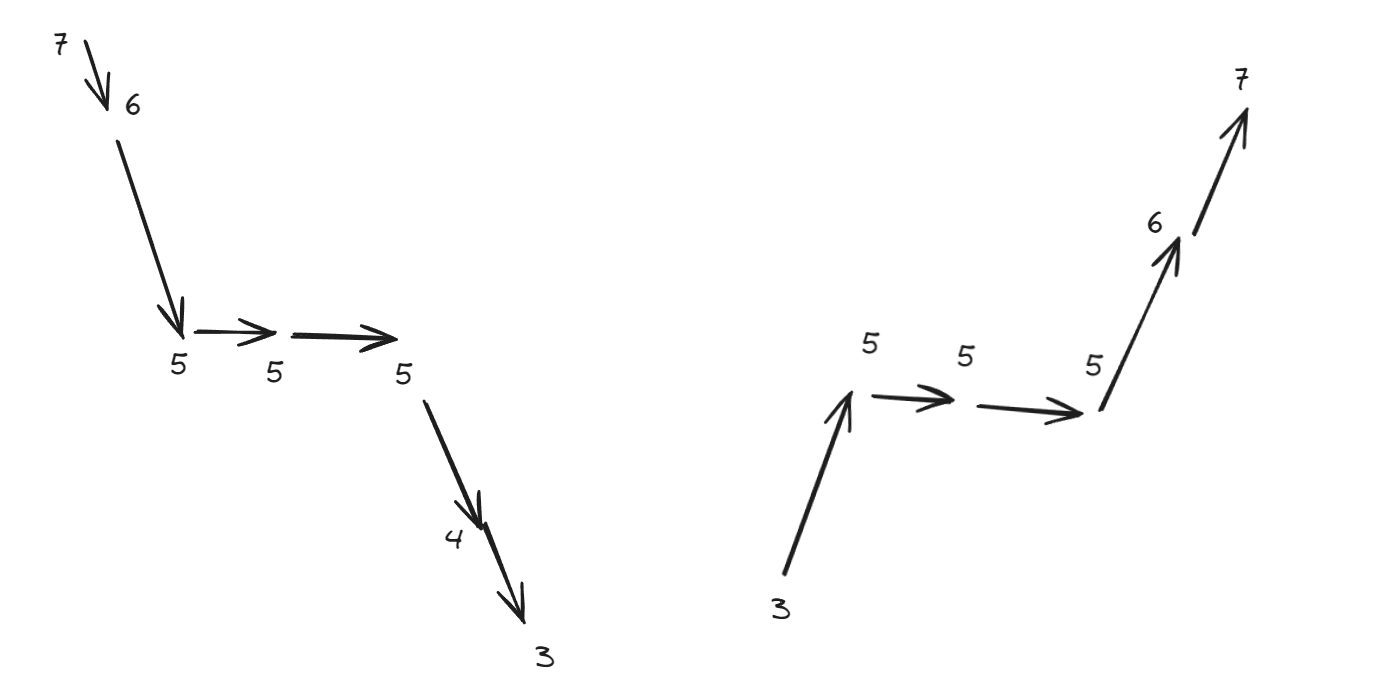
- 将题目中的摆动抽象成上升沿与下降沿,会方便理解。
- 此题要考虑的情况非常多,一次性考虑清楚真的非常难。debug了一个多小时才把所有情况补上

- 只有一个元素
- 只有两个元素,且元素不相同
- 只有两个元素,且元素相同
- 大于两个元素,且元素都相同
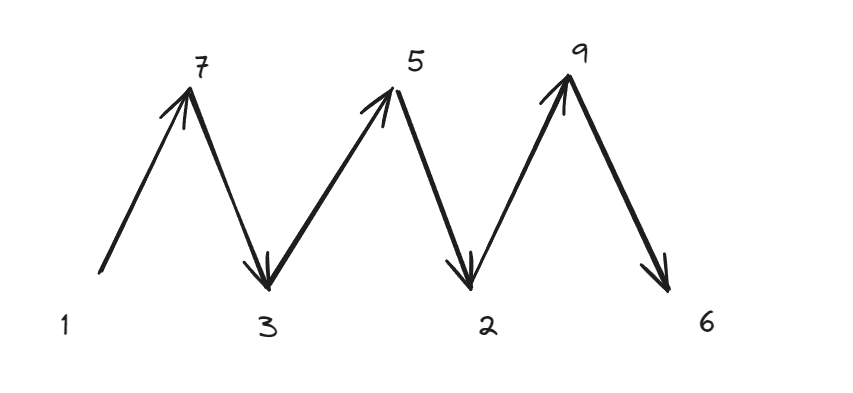
- 大于两个元素,元素相邻之间互不相同
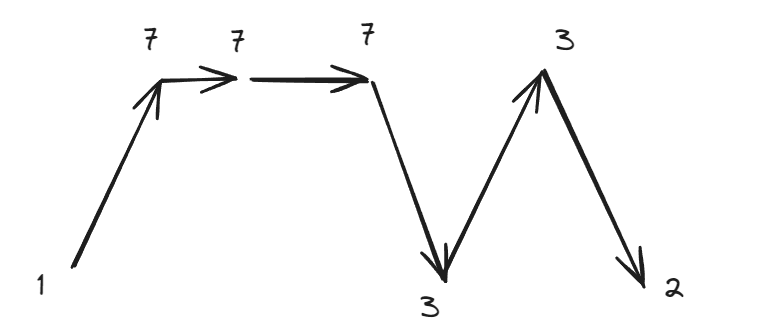
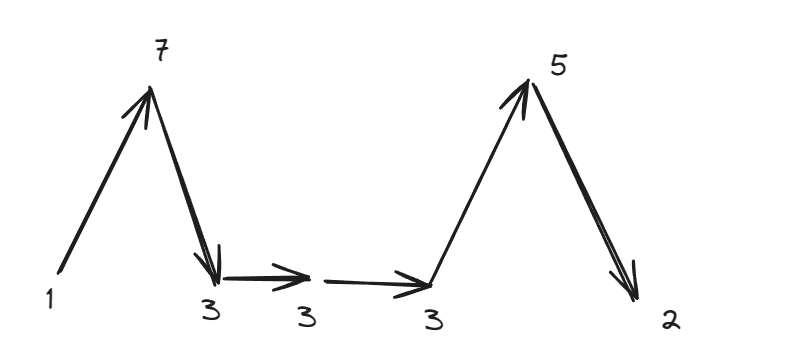
- 大于两个元素,元素相邻之间有部分相同
- 大于两个元素,单调递增/递减,元素相邻互不相同
- 大于两个元素,单调递增/递减,元素相邻有部分相同
- 默认两边是存在两个子序列长度的,所以子序列长度count从2开始递增,循环遍历从1开始,一直到count(nums)-2,遇到一个顶峰(上顶峰或者下顶峰)count++即可。需要特殊处理,中间有相同元素的情况,因为即使有相同元素梯形也只算一个序列长度,所以使用while跳过相同元素后,判断趋势是否相反,相反count++,同时更新循环索引i,避免重复循环即可。
复杂度
时间复杂度
O(n)
空间复杂度
O(1)
code
class Solution {
/**
* @param Integer[] $nums
* @return Integer
*/
function wiggleMaxLength($nums) {
if(count($nums) == 1) return 1;
if(count($nums) == 2){
//两个元素互不相同的情况
if($nums[0] != $nums[1]){
return 2;
}else{
return 1;
}
}
//nums元素都相同的情况
$check = array_unique($nums);
if(count($check) == 1) return 1;
$i = 1;//默认第一位是一个子序列长度,所以从1开始
$count = 2;//默认首尾等于两个子序列长度,所以count从2开始
//默认末尾为一个子序列长度,所以只遍历到count($nums) - 1停止即可,否则会溢出
while($i < count($nums) - 1){
//左右相邻不相等的情况 且当前为上顶峰的情况
if($nums[$i] - $nums[$i-1] > 0 && $nums[$i + 1] - $nums[$i] < 0){
$count++;
}
//左右相邻不相等的情况 且当前为下顶峰的情况
if($nums[$i] - $nums[$i-1] < 0 && $nums[$i + 1] - $nums[$i] > 0){
$count++;
}
//下一个是相同元素 且当前为下降沿的情况
if($nums[$i] - $nums[$i-1] < 0 && $nums[$i + 1] == $nums[$i]){
$j = $i + 2;
//获取下一个不同的值
while($j < count($nums) - 1 && $nums[$i] == $nums[$j]){
$j++;
}
//判断与当前趋势不同则++,并且更新i
if($nums[$j] > $nums[$i]){
$count++;
$i = $j - 1;//因为下面有i++所以需要-1,否则就跳过$nums[$j] 元素了;
}
}
//下一个是相同元素 且当前为上升沿的情况
if($nums[$i] - $nums[$i-1] > 0 && $nums[$i + 1] == $nums[$i]){
$k = $i + 2;
//获取下一个不同的值
while($k < count($nums) - 1 && $nums[$i] == $nums[$k]){
$k++;
}
//判断与当前趋势不同则++,并且更新i
if($nums[$k] < $nums[$i]){
$count++;
$i = $k - 1;//因为下面有i++所以需要-1,否则就跳过$nums[$j] 元素了;
}
}
$i++;
}
return $count;
}
}53. 最大子数组和
注意的地方
- 子数组是数组中的一个连续部分。
- 子数组最少包含一个元素。
解题方法
- 如果 -2 1 在一起,计算起点的时候,一定是从 1 开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
- 局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
- 全局最优:选取最大“连续和”、局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
- 从代码角度上来讲:遍历 nums,从头开始用 count 累积,如果 count 一旦加上 nums[i]变为负数,那么就应该从 nums[i+1]开始从 0 累积 count 了,因为已经变为负数的 count,只会拖累总和。
复杂度
时间复杂度
O(n)
空间复杂度
O(1)
code
class Solution {
/**
* @param Integer[] $nums
* @return Integer
*/
function maxSubArray($nums) {
$max = PHP_INT_MIN;
$count = 0;
for($i = 0; $i < count($nums); $i++){
$count += $nums[$i];
//更新最大值
$max = max($max, $count);
//当前连续和小于0,则丢弃,从下一个元素开始累加。因为负数加上任何数都会比原来小。
if($count < 0) $count = 0;
}
return $max;
}
}本作品采用《CC 协议》,转载必须注明作者和本文链接


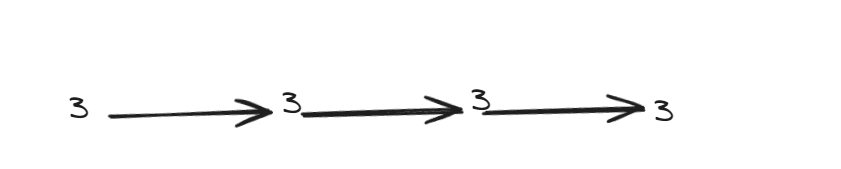




 关于 LearnKu
关于 LearnKu



