代码随想录算法训练营第四十四天 | leetcode：最长公共子序列,不相交的线 ,最大子序和
0 / 0 / 创建于 1年前 /
_zzh 的个人博客
1143. 最长公共子序列#
解题方法#
- dp 数组的含义：dp [i][j]：长度为 [0, i - 1] 的字符串 text1 与长度为 [0, j - 1] 的字符串 text2 的最长公共子序列为 dp [i][j]
- 确定递推公式：主要就是两大情况： text1 [i - 1] 与 text2 [j - 1] 相同，text1 [i - 1] 与 text2 [j - 1] 不相同
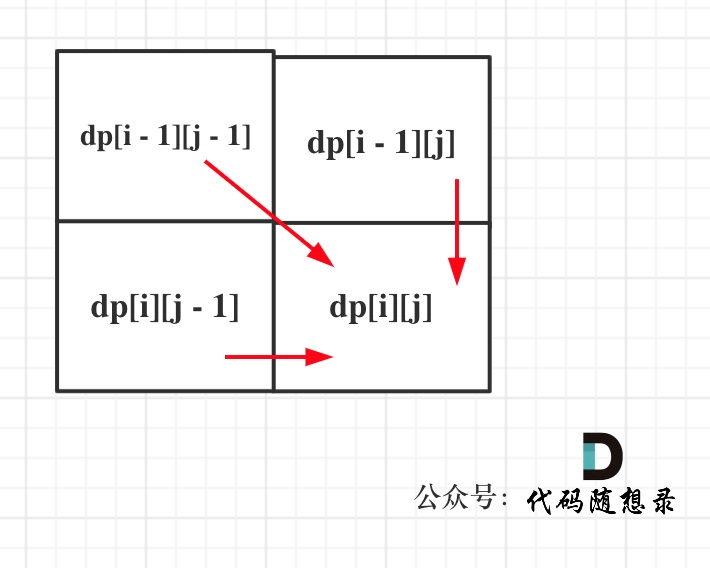
- 情况 1：如果 text1 [i - 1] 与 text2 [j - 1] 相同，那么找到了一个公共元素，所以 dp[i][j] = dp[i - 1][j - 1] + 1;
- 情况 2：如果 text1 [i - 1] 与 text2 [j - 1] 不相同，那就看看 text1 [0, i - 2] 与 text2 [0, j - 1] 的最长公共子序列 和 text1 [0, i - 1] 与 text2 [0, j - 2] 的最长公共子序列，取最大的。即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
- 初始化 dp 数组：根据 dp 数组的含义（长度为 [0, i - 1] 的字符串 text1，长度为 [0, j - 1] 的字符串 text2），当 dp [i][0]/dp [0][j] 时，就会出现有负数的情况，所以需要初始化为 0，其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为 0。
- 遍历顺序：从递推公式，可以看出，有三个方向可以推出 dp [i][j]，所以要从前向后，从上到下来遍历。
code#
class Solution {
/**
* @param String $text1
* @param String $text2
* @return Integer
*/
function longestCommonSubsequence($text1, $text2) {
$len1 = strlen($text1);
$len2 = strlen($text2);
$dp = array_fill(0, $len1+1, array_fill(0, $len2+1, 0));
//print_r($dp);
for($i = 1; $i <= $len1; $i++){
for($j = 1; $j <= $len2; $j++){
if($text1[$i-1] == $text2[$j-1]){
//对应情况1
$dp[$i][$j] = $dp[$i-1][$j-1] + 1;
}else{
//对应情况2
$dp[$i][$j] = max($dp[$i-1][$j],$dp[$i][$j-1]);
}
}
}
return $dp[$len1][$len2];
}
}复杂度#
时间复杂度
O (n x m) 其中 n 和 m 分别为 text1 和 text2 的长度
空间复杂度
O(n x m)
1035. 不相交的线#
解题方法#
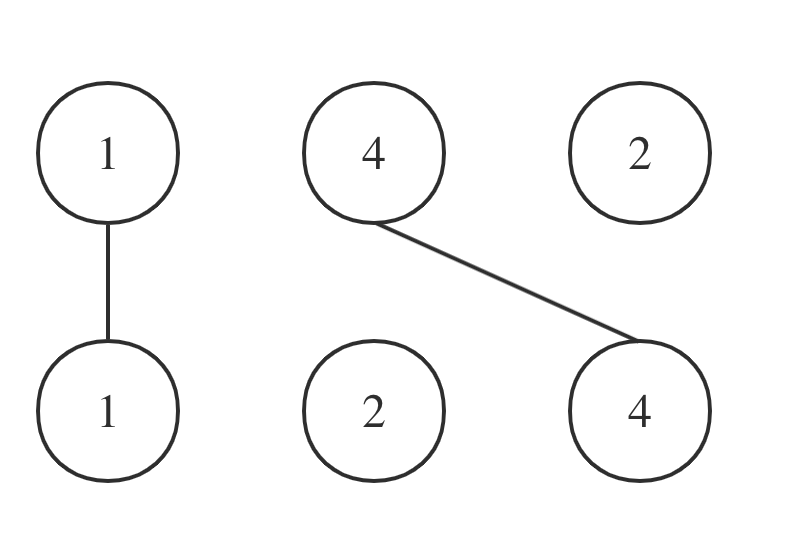
绘制一些连接两个数字 A [i] 和 B [j] 的直线，只要 A [i] == B [j]，且直线不能相交！
直线不能相交，这就是说明在字符串 A 中 找到一个与字符串 B 相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。
也就是说 A 和 B 的最长公共子序列是 [1,4]，长度为 2。 这个公共子序列指的是相对顺序不变（即数字 4 在字符串 A 中数字 1 的后面，那么数字 4 也应该在字符串 B 数字 1 的后面，可以发现：本题说是求绘制的最大连线数，其实就是和上题一样求两个字符串的最长公共子序列的长度！，代码都是一样的。
53. 最大子数组和#
解题方法#
- dp 数组的含义：dp [i] ：以 nums [i] 结尾的最大连续子数组和为 dp [i]
- 确定递推公式：dp[i] = max(dp[i - 1] + nums[i], nums[i]);
- dp [i-1] + nums [i]: 表示延续 nums 子数组
- nums [i]: 表示舍弃 i-1 及之前的结果，重新开始计算
- 初始化 dp 数组：dp [0] = nums [0]；其余值初始化为 0；
- 遍历顺序：递推公式中 dp [i] 依赖于 dp [i - 1] 的状态，需要从前向后遍历。
code#
class Solution {
/**
* @param Integer[] $nums
* @return Integer
*/
function maxSubArray($nums) {
/**
dp[i] : 以nums[i]结尾的最大连续子数组和为dp[i]
dp[i] = max(dp[i-1] + nums[i], nums[i])
dp[i-1] + nums[i]:表示延续nums子数组
nums[i]:表示舍弃i-1及之前的结果，重新开始计算
*/
$len = count($nums);
if($len == 1) return $nums[0];
$dp = array_fill(0, $len, 0);
$dp[0] = $nums[0];
$res = $nums[0];
for($i = 1; $i < $len; $i++){
$dp[$i] = max($dp[$i - 1] + $nums[$i], $nums[$i]);
if($dp[$i] > $res) $res = $dp[$i]; //获取dp[i]最大值
}
return $res;
}
}复杂度#
时间复杂度
O(n)
空间复杂度
O(n)
本作品采用《CC 协议》，转载必须注明作者和本文链接
关于 LearnKu
粤公网安备 44030502004330号
推荐文章：