代码随想录算法训练营第三十三天 | leetcode：整数拆分,不同二叉搜索树
0 / 0 / 创建于 11个月前
_zzh 的个人博客
343. 整数拆分
解题方法
- dp[i] = 分拆数字i，可以得到的最大乘积为dp[i]
- dp[i] = max(max(i x (i-j), j x dp[i-j]), dp[i]),
其中i x (i-j)为拆分两个数的情况，j x dp[i-j]为两个以上的数，j * dp[i - j]相当于是拆分(i - j)，对这个拆分不理解的话，可以回想dp数组的定义- 因为2 <= n <= 58， 所以初始化 dp[2] = 1即可
- 遍历顺序：dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]。
code
class Solution {
/**
* @param Integer $n
* @return Integer
*/
function integerBreak($n) {
$dp = [];
$dp[2] = 1;
for($i = 3; $i <= $n; $i++){
//每次拆分都需要靠近i/2才有可能获得最大
for($j = 1; $j <= $i/2; $j++){
$dp[$i] = max($dp[$i], max($j * ($i - $j), $j * $dp[$i - $j]));
}
}
return $dp[$n];
}
}复杂度
时间复杂度
O(m x n)
空间复杂度
O(m x n)
Problem: 96. 不同的二叉搜索树
解题方法
- dp[i]: 当有i个节点时，最多能有dp[i]种不同的二叉搜索树
- 推导递推公式（超级难点，根本想不到）：
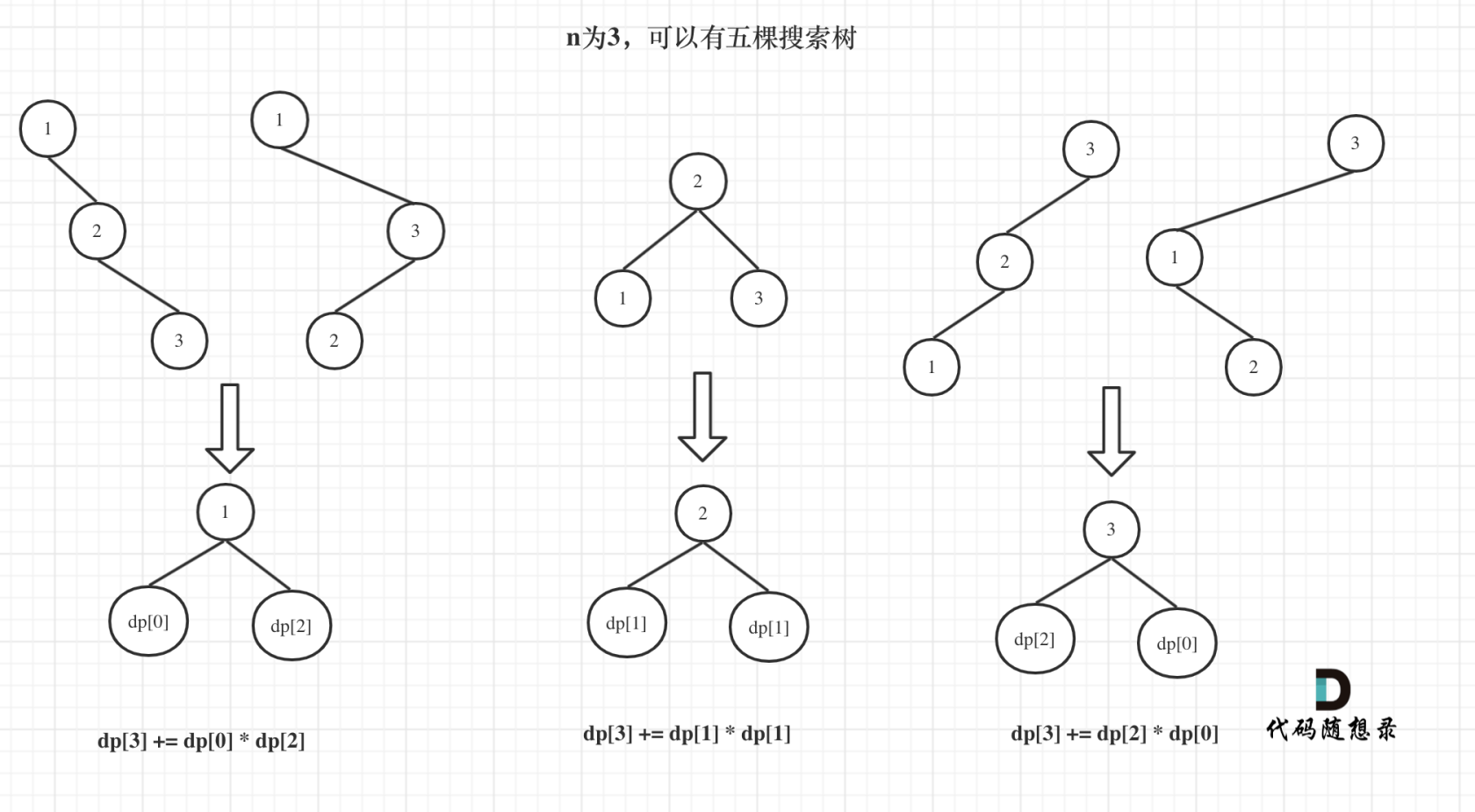
- dp[i] = 累计当头结点为1-n的情况。 举例：n=3。dp[i] = 头结点=1的数量的情况 + 头结点=2的情况 + 头结点=3的情况。
- 二叉树确定头结点的情况下有多少种组合方式呢，是等于左子树的组合方式 * 右子树的组合方式。
- 即：
- 当n=3，头结点=1时： 左子树节点为空 = 0：组合方式只有1种，右子树节点为2： 有2种组合方式。总共有1 x 2种组合方式
- 当n=3，头结点=2时：左子树节点 = 1 组合方式只有1种, 右子树节点数 = 1,组合方式只有1种,；总共有1 x 1一种组合方式
- 当n=3，头结点=3时：左子树节点 = 2 组合方式有2种, 右子树节点数 = 0,组合方式只有1种；总共有2 x 1一种组合方式
- 由上可得 ：dp[3] = 2 + 1 + 2 = 5；
- 同时：左子树与右子树也算二叉搜索树，也就是说，左子树和右子树也可以用dp数组表示。
- 例如当n=3，头结点=1时，左子树节点为空 = 0的情况等于$n=0 即dp[0]的情况。
- 右子树节点为2 等于$n=2 即dp[2]的情况。
- 可得：dp[3] = dp[0] * dp[2] + dp[1] * dp[1] + dp[2] * dp[0];
- dp[i] += dp[j - 1] * dp[i - j]; 其中j为头结点，j - 1为左孩子节点，i - j为右孩子节点，j <= i
- 初始化dp数组，dp[0] = 1即可。因为当i = j = 1时，用dp[0]就可推导出结果： dp[1] = dp[1-1] * dp[1-1]。
- 因为i 依赖与前面的数据，所以遍历顺序是从小到大
code
/**
* @param Integer $n
* @return Integer
*/
function numTrees($n) {
$dp = [];
$dp[0] = 1;
for($i = 1; $i <= $n; $i++){
for($j = 1; $j <= $i; $j++){
//因为是累计所以这里是+=
$dp[$i] += $dp[$j - 1] * $dp[$i - $j];
}
}
return $dp[$n];
}
}复杂度
时间复杂度
O(n^2)
空间复杂度
O(n)
本作品采用《CC 协议》，转载必须注明作者和本文链接
关于 LearnKu
粤公网安备 44030502004330号