代码随想录算法训练营第二十天 | leetcode：回溯算法理论基础,组合问题
0 / 0 / 创建于 1年前
_zzh 的个人博客
前段时间有事，落下了不少二叉树章节。所以跳级更新回溯算法，后续抽空再补上落下的章节。
回溯算法理论基础
- 回溯法也可以叫做回溯搜索法，它是一种搜索的方式。回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案。与暴力for循环没啥本质区别，只是使用递归省略了多层嵌套的情况。所以可以大概的理解为，回溯算法是for+递归。回溯法解决的问题可以抽象为树形结构for遍历第一层横向，递归遍历纵向。想象遍历多个二叉树，应该比较好理解。
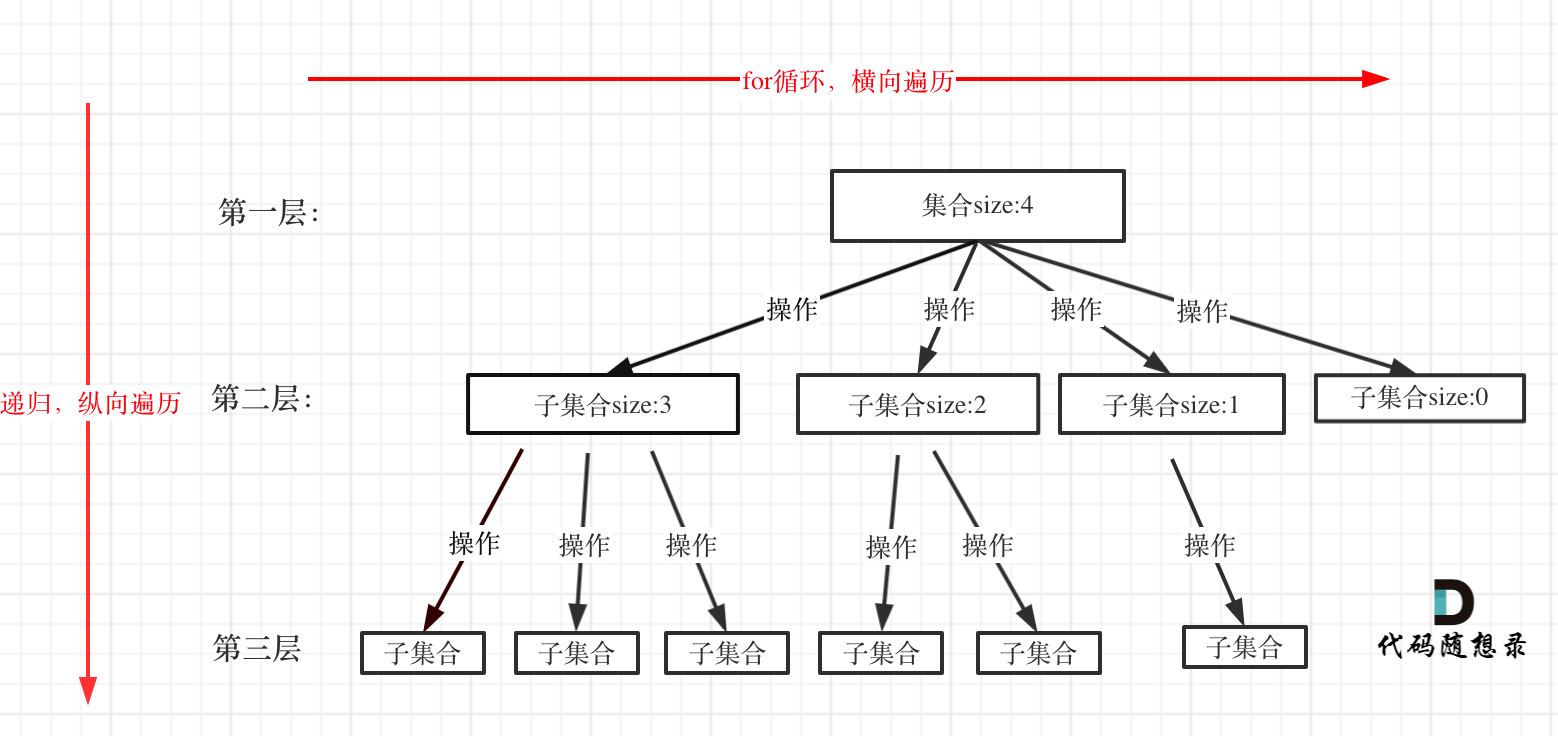
回溯法，一般可以解决如下几种问题：
- 组合问题：N个数里面按一定规则找出k个数的集合
- 切割问题：一个字符串按一定规则有几种切割方式
- 子集问题：一个N个数的集合里有多少符合条件的子集
- 排列问题：N个数按一定规则全排列，有几种排列方式
- 棋盘问题：N皇后，解数独等等
附上卡哥总结的回溯模板，嘎嘎好用
。void backtracking(参数) { if (终止条件) { 存放结果; return; } for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) { 处理节点; backtracking(路径，选择列表); // 递归 回溯，撤销处理结果 } }Problem: 77. 组合
注意的地方
回溯算法可以进行剪枝操作进行优化，即：当剩余元素比组合数k小时可以跳出for循环。举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。
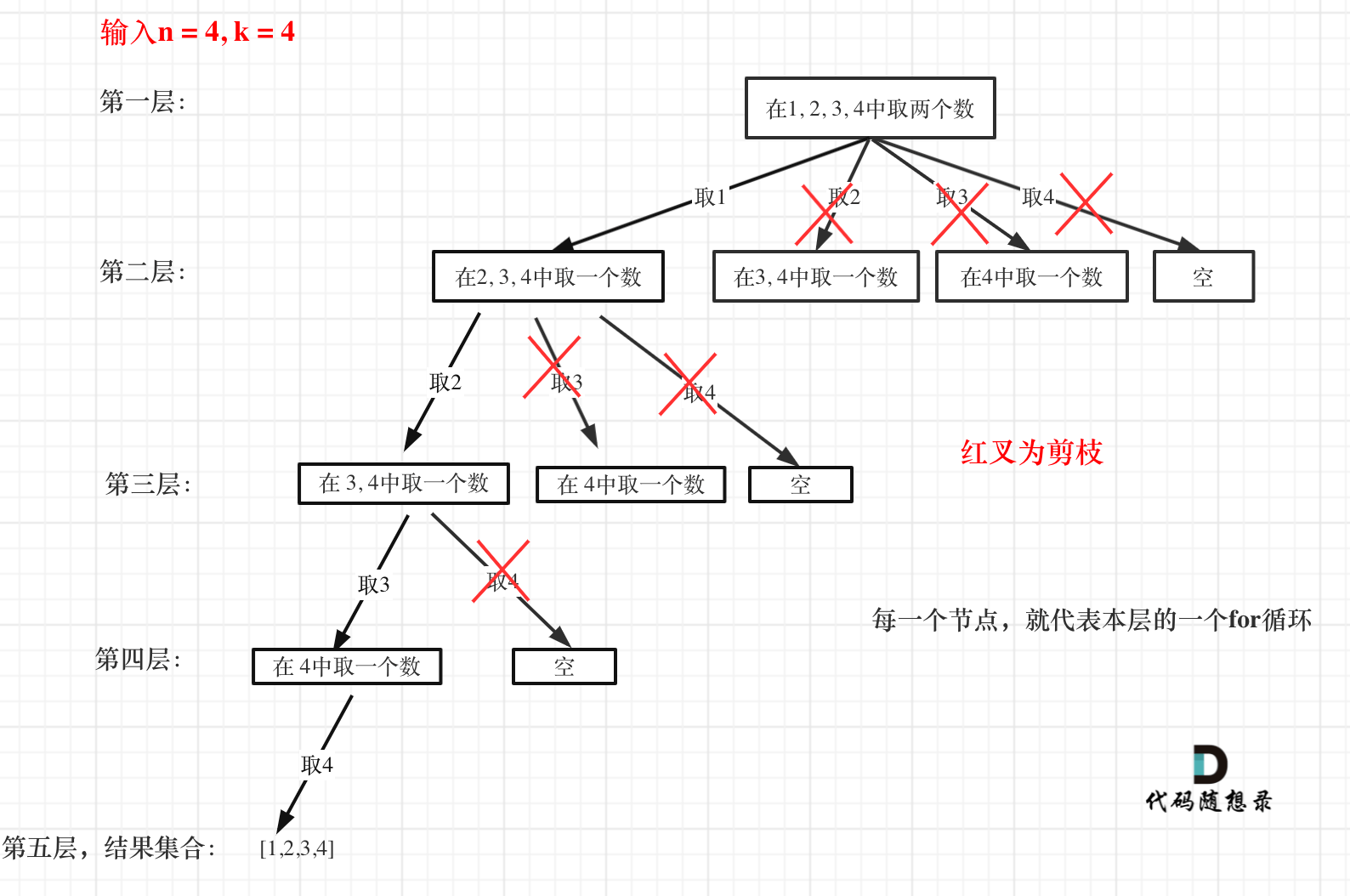
code
class Solution {
private $res = [];//二位数组结果集
private $path = [];//单次结果集
/**
* @param Integer $n
* @param Integer $k
* @return Integer[][]
*/
function combine($n, $k) {
$this->backtracking($n, $k, 1);
return $this->res;
}
function backtracking($n, $k, $startIndex){
//判断当前组合是否等于k组合数长度
if(count($this->path) == $k){
//把path结果存入目标数组
$this->res[] = $this->path;
return;
}
//对进行外层循环 循环n次
$pathLen = count($this->path);
//还需要的元素个数为: k - $pathLen; 总共还剩下多少个元素：$n-($k-$pathLen); 因为包括起始位置所以需要+1
for($i = $startIndex; $i <= $n-($k-$pathLen)+1; $i++){
//把组合元素放进数组
$this->path[] = $i;
//下一次循环从下一个数开始，所以$startIndex = $i+1
$this->backtracking($n, $k, $i+1);
//当i=4时，触发一次递归的回溯，一次for循环结束的回溯
array_pop($this->path);
}
}
}本作品采用《CC 协议》，转载必须注明作者和本文链接
关于 LearnKu
粤公网安备 44030502004330号