定积分

定积分几何定义#

我们把定积分理解成求曲线下面积的计算方法。

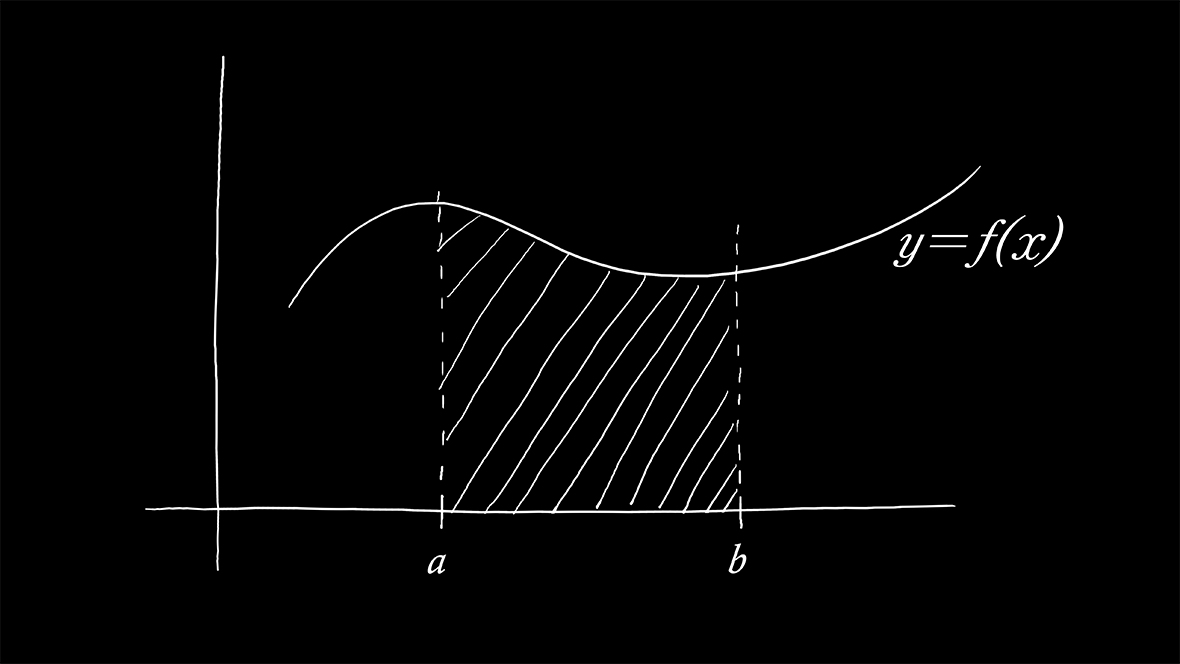
上图中阴影部分的面积是：

$\displaystyle \int_a^bf(x)dx$

定积分和不定积分不同，定积分没有上下限，定积分有上下限，在这个式子里$a$ 是积分下限，$b$ 是积分上限。
我们来看下这样求面积的原理：

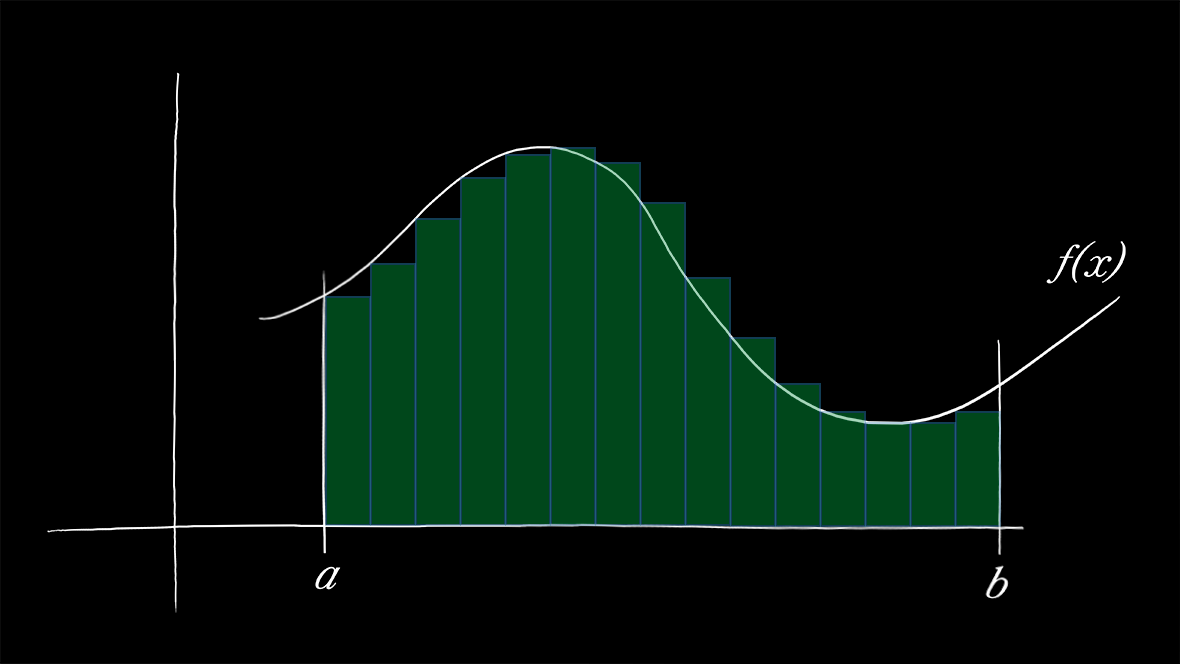
我们凭直觉看看图中的绿色矩形们的面积加起来与曲线下面积是有误差的。
我们再来看图：

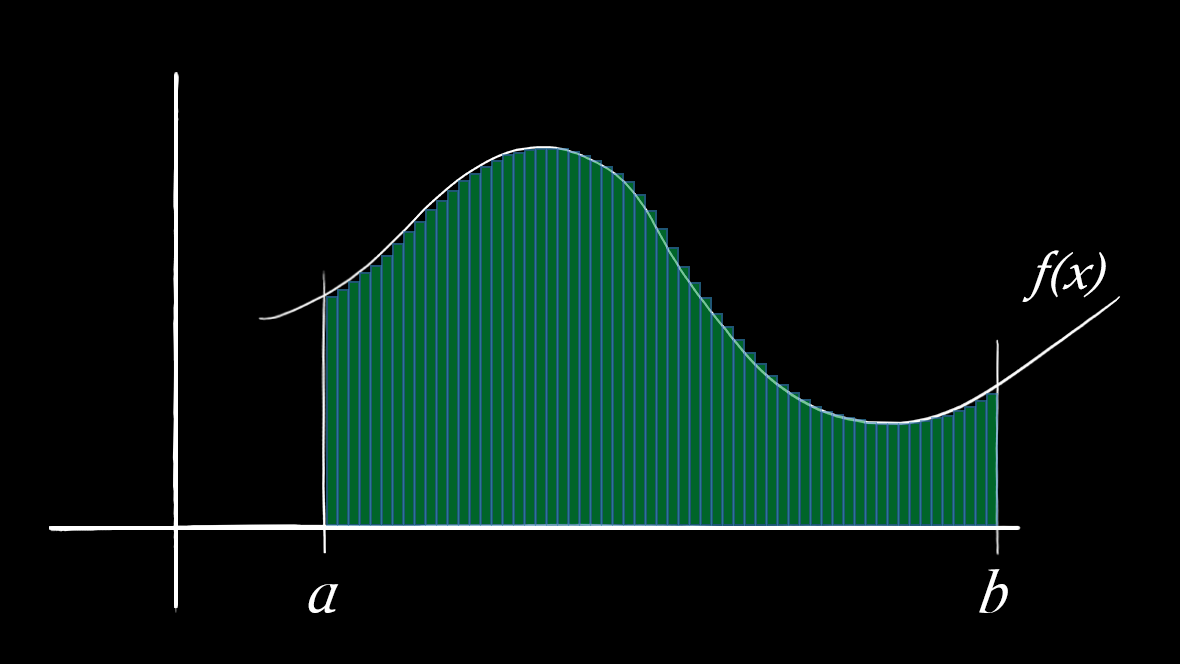
这图看起来矩形面积和与曲线下面积误差小很多。

求曲线下面积分三步走：

1. 首先把它切割成一些 “矩形”。
2. 把这些矩形的面积加起来。
3. 通过矩形变窄来取得极限值。

来测试下三角形吧，我们看函数$\displaystyle f(x)=\frac{1}{2}x$。

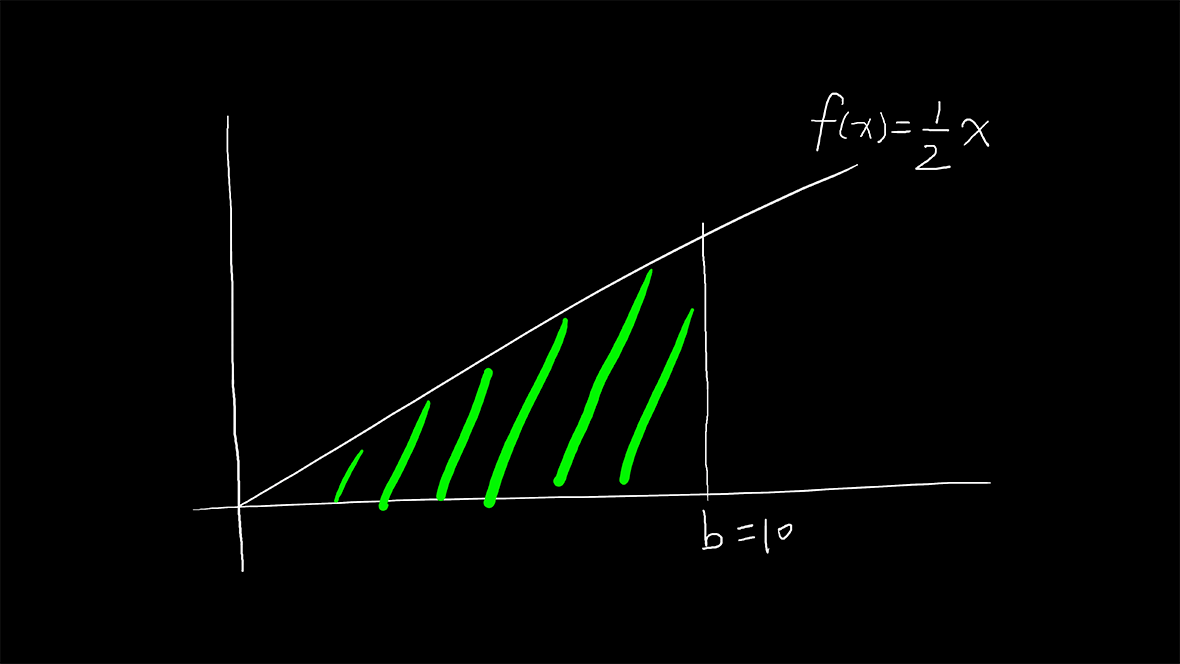
为了方便计算，我直接把$a$ 设成$0$，我们先用古老的方法来算一下绿色三角形面积，三角形面积等于底乘以高除以$2$。

$\displaystyle area=\frac{b\cdot f(b)}{2}=\frac{1}{2}\cdot10\cdot\frac{10}{2}=25$

再来试试矩形面积累加和的计算方式：

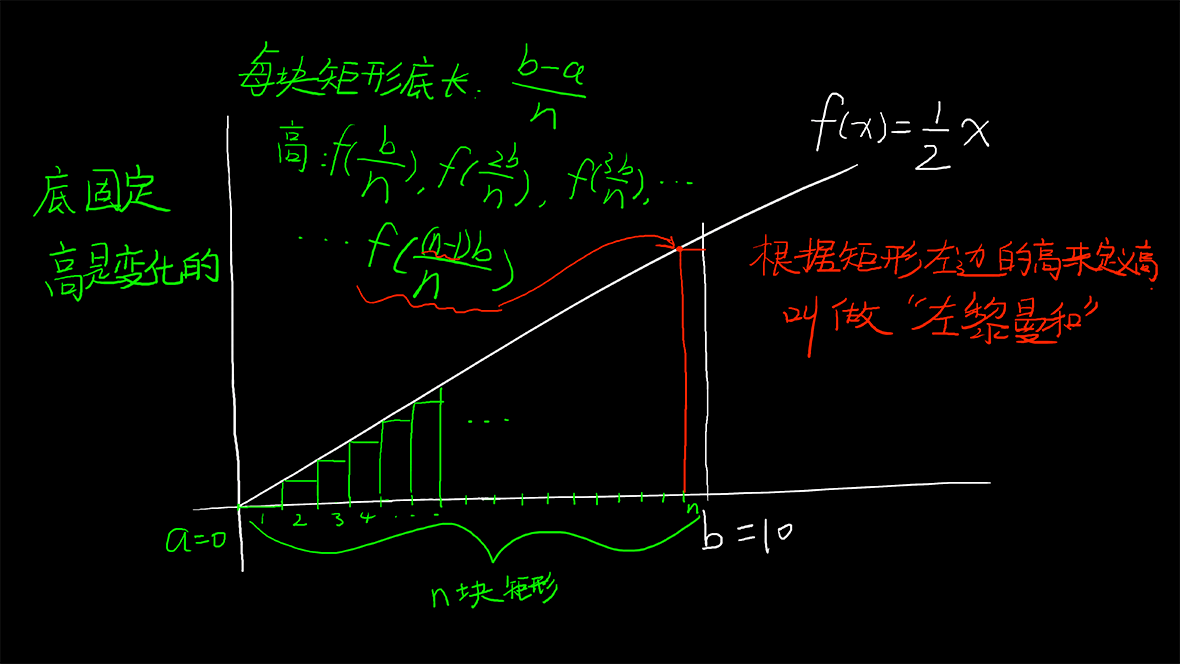
计算矩形面积的高有两种定义方法，这里我们采取的是「左黎曼和」切割方式。可以看到第一块矩形的高是$0$，因为$a=0$，我们按照每一块的矩形左边对应的函数值来计算，而第一块矩形的左边刚好是在$f(a)$ 处，而$f(a)=0$。
我们来计算下矩形面积和，由于$a=0$，所以$b-a$ 直接写成$b$。

$\displaystyle _{leftsum}area=\frac{b}{n}\cdot f(\frac{b}{n})+\frac{b}{n}\cdot f(\frac{2b}{n})+\\{}\\ ...+\frac{b}{n}\cdot f(\frac{(n-1)b}{n})\\{}\\ =\frac{b}{n}\cdot\frac{1}{2}\cdot\frac{b}{n}+\frac{b}{n}\cdot\frac{1}{2}\cdot\frac{2b}{n}+\\{}\\ ...+\frac{b}{n}\cdot\frac{1}{2}\cdot\frac{(n-1)b}{n}\\{}\\ =\frac{b}{2n}\sum_{j=1}^{n-1}\frac{jb}{n}$

我们先分个十块试试：

$\displaystyle \frac{b}{2n}\sum_{j=1}^{n-1}\frac{jb}{n}\bigg|_{n=10}=\frac{10}{20}\sum_{j=1}^9\frac{10j}{10}\\{}\\ =\frac{1}{2}\cdot(1+2+3+...+9)\\{}\\ =\frac{1}{2}\cdot\frac{9(1+9)}{2}\\{}\\ =\frac{45}{2}=22.5$

我们再分二十块试试：

$\displaystyle \frac{b}{2n}\sum_{j=1}^{n-1}\frac{jb}{n}\bigg|_{n=20}=\frac{10}{40}\sum_{j=1}^{19}\frac{10j}{20}\\{}\\ =\frac{1}{8}\cdot(1+2+3+...+19)\\{}\\ =\frac{1}{8}\cdot\frac{19(1+19)}{2}\\{}\\ =\frac{190}{8}=23.75$

我们再分一百块试试：

$\displaystyle \frac{b}{2n}\sum_{j=1}^{n-1}\frac{jb}{n}\bigg|_{n=100}=\frac{10}{200}\sum_{j=1}^{99}\frac{10j}{100}\\{}\\ =\frac{1}{200}\cdot(1+2+3+...+99)\\{}\\ =\frac{1}{200}\cdot\frac{99(1+99)}{2}\\{}\\ =\frac{4950}{200}=24.75$

我们发现分的越多，矩形和面积值越接近三角形面积值，但永远都是小于三角形面积值的，因为我们用的是左黎曼和。
我们来试试右黎曼和：

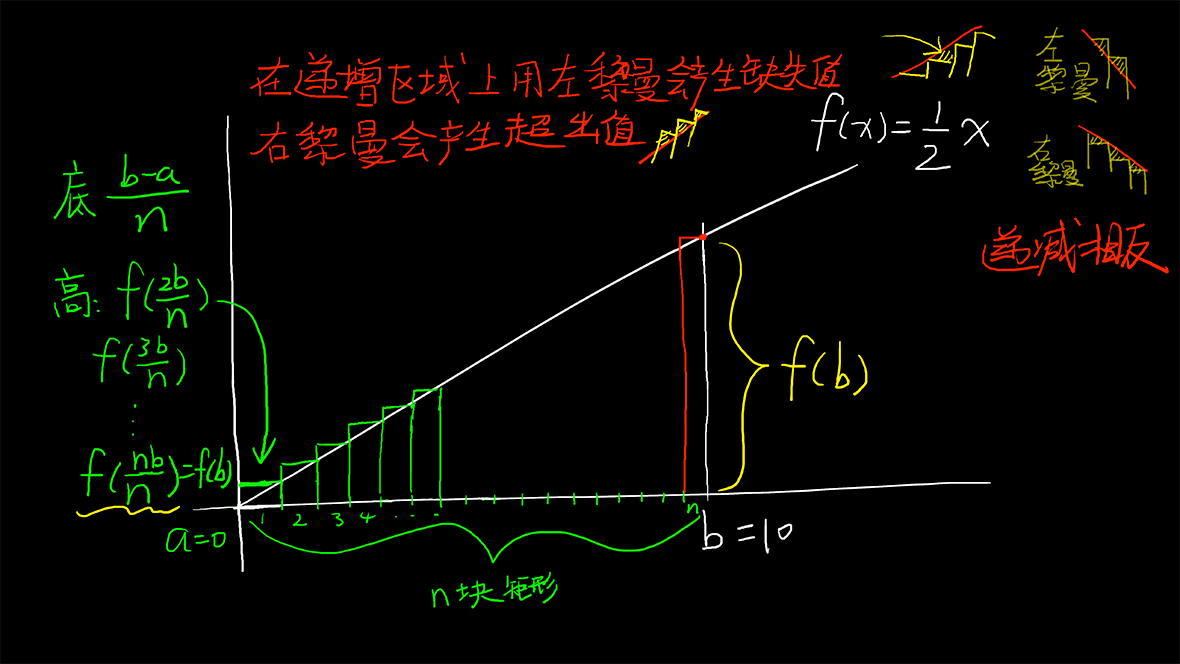
$\displaystyle _{rightsum}area=\frac{b}{2n}\sum_{j=2}^n\frac{jb}{n}\\{}\\$

分二十块试试：

$\displaystyle \frac{b}{2n}\sum_{j=2}^n\frac{jb}{n}\bigg|_{n=20}=\frac{10}{40}\sum_{j=2}^{20}\frac{10j}{20}\\{}\\ =\frac{1}{8}\cdot(2+3+4+...+20)\\{}\\ =\frac{1}{8}\cdot\frac{19(2+20)}{2}\\{}\\ =\frac{19+190}{8}\\{}\\ =26.125$

分一百块试试：

$\displaystyle \frac{b}{2n}\sum_{j=2}^n\frac{jb}{n}\bigg|_{n=100}=\frac{10}{200}\sum_{j=2}^{100}\frac{10j}{100}\\{}\\ =\frac{1}{200}\cdot(2+3+4+...+100)\\{}\\ =\frac{1}{200}\cdot\frac{99(2+100)}{2}\\{}\\ =\frac{198+9900}{400}\\{}\\ =25.245$

现在我们来计算下函数$f(x)=x^2$ 曲线下面积吧：

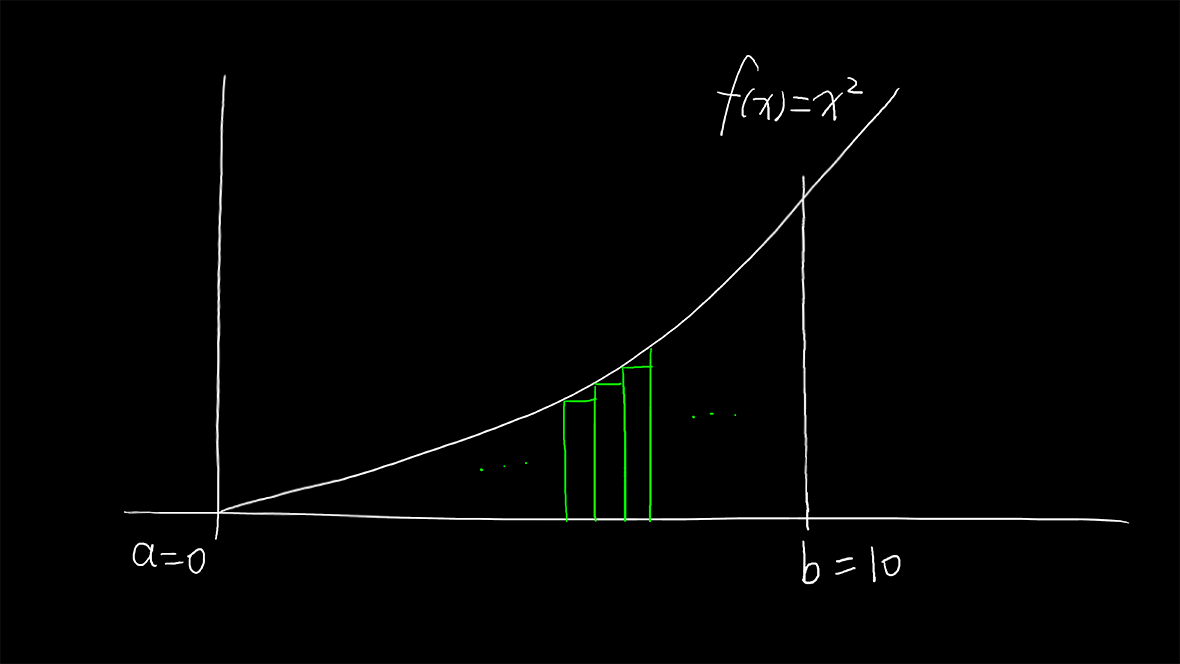
我们直接用左黎曼和$1$ 到$n-1$。（右黎曼和$2$ 到$n$）

$\displaystyle _{leftsum}area=\frac{b}{n}\cdot f(\frac{b}{n})+\frac{b}{n}\cdot f(\frac{2b}{n})+\\{}\\ ...+\frac{b}{n}\cdot f(\frac{(n-1)b}{n})\\{}\\ =\frac{b}{n}\cdot\left(\frac{b}{n}\right)^2+\frac{b}{n}\cdot\left(\frac{2b}{n}\right)^2+\\{}\\ ...+\frac{b}{n}\cdot\left(\frac{(n-1)b}{n}\right)^2\\{}\\ =\frac{b}{n}\cdot\sum_{j=1}^{n-1}\left(\frac{jb}{n}\right)^2\\{}\\$

分成十块矩形试试：

$\displaystyle \frac{b}{n}\cdot\sum_{j=1}^{n-1}\left(\frac{jb}{n}\right)^2\bigg|_{n=10}=\frac{10}{10}\cdot\sum_{j=1}^{9}\left(\frac{10j}{10}\right)^2\\{}\\ =\sum_{j=1}^{9}j^2=285$

现在我们来换另一种理解方式：

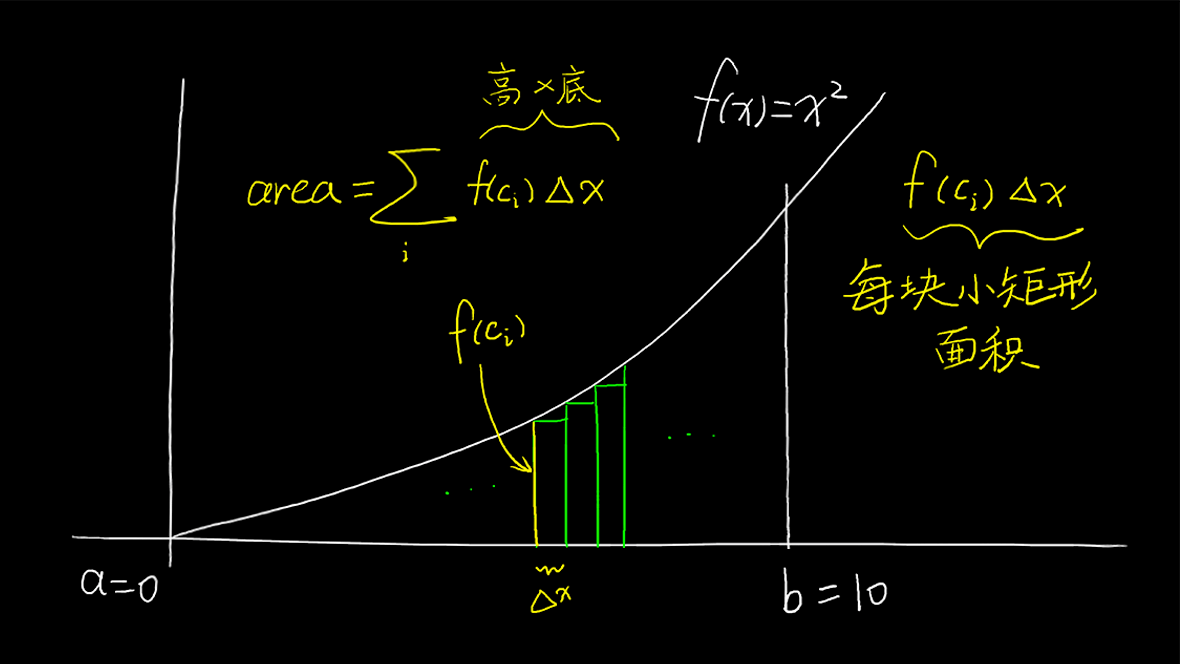
我们把每块小矩形的高记作$f(c_i)$，把每块小矩形的高记作$\displaystyle\Delta x=\frac{b-a}{n}$，那么曲线下的近似面积为一系列离散值的和，我们现在把离散的求和式映射到连续的积分式也就是另$\Delta x\to0$ 记作$dx$：

$\displaystyle \sum_{i=1}^nf(c_i)\Delta x\Longrightarrow\int_a^bf(x)dx$

这里的求和式我没有用左黎曼和，而是直接用的$1$ 到$n$，对应图如图所示：

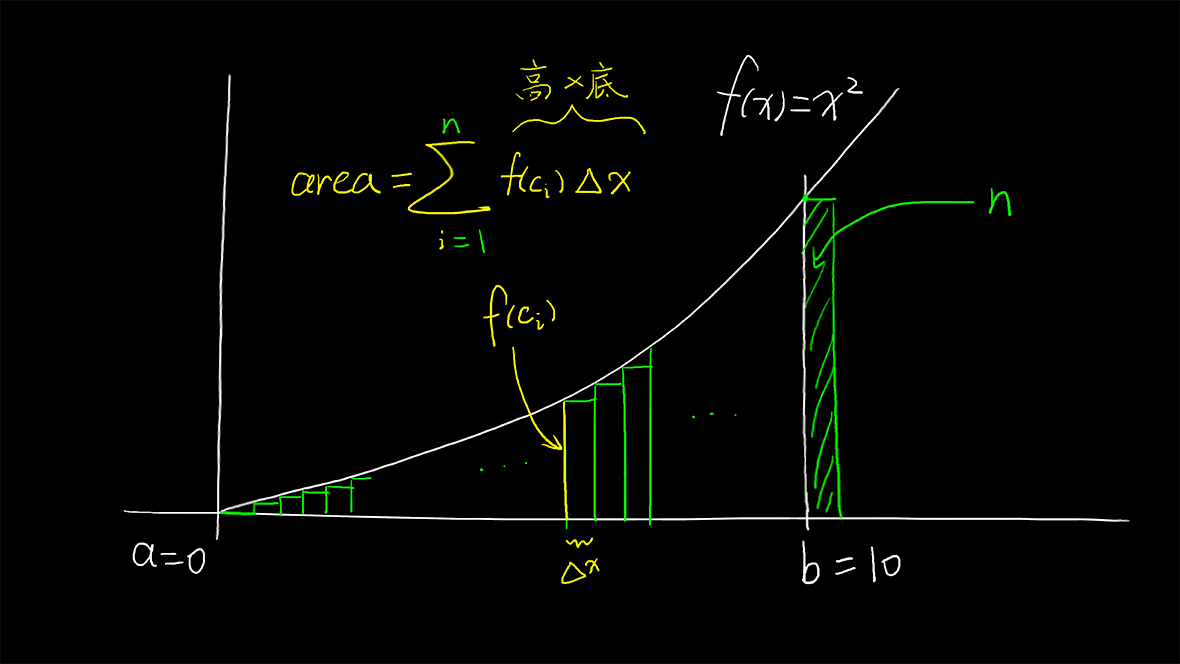
右边超出去了一个矩形，不过这没关系，我们具备宽度的$\Delta x$ 变成了不具备具宽度的无穷小量$dx$，我们的有限的离散矩形变成了无限的连续点，所以高度可以直接用函数值$f(x)$ 来代替，定积分可以理解成求和的连续版本。

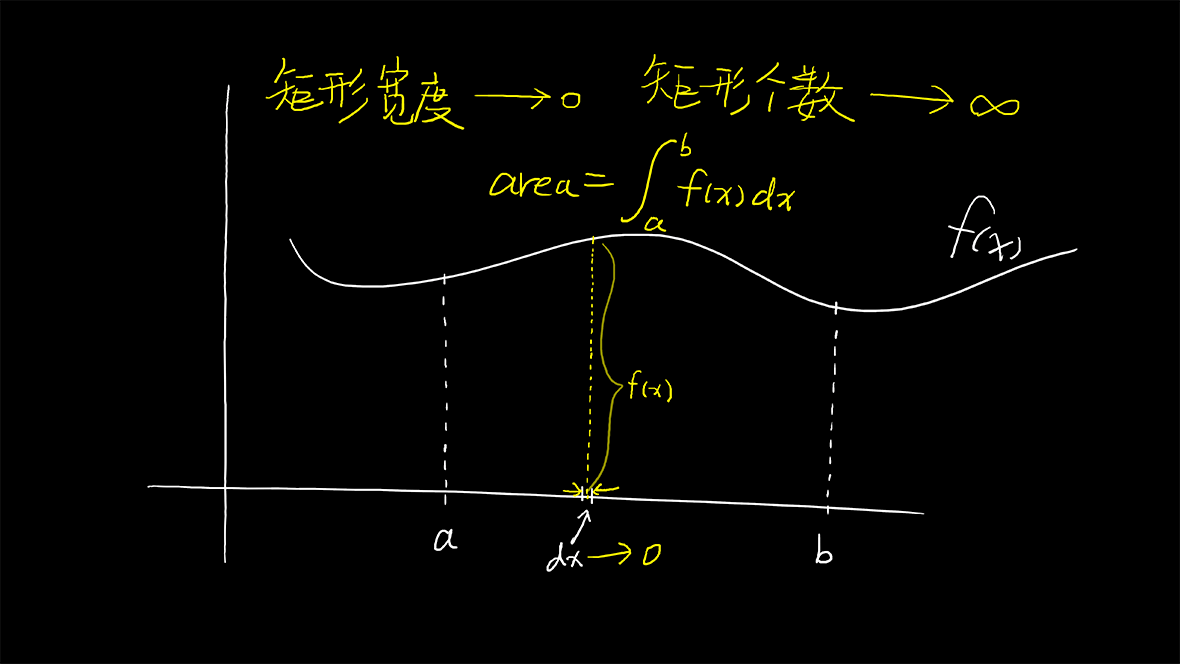
我们来验证一下之前的三角形面积：

$\displaystyle area=\int_a^bf(x)dx=\int_0^{10}\frac{xdx}{2}\\{}\\ =\frac{x^2}{4}\bigg|_0^{10}=\frac{10^2}{4}-\frac{0^2}{4}=25$

注意，定积分是没有常数$c$ 的，因为上下限相减，抵消掉了。
我们顺便再来看下$x^2$ 曲线下面积吧：

$\displaystyle area=\int_a^bf(x)dx=\int_0^{10}x^2dx\\{}\\ =\frac{x^3}{3}\bigg|_0^{10}=\frac{10^3}{3}-\frac{0^3}{3}=333.\dot{3}$