MVT 中值定理
中值定理(MVT)
说到中值定理,肯定会关系到:
- 费马定理
- 罗尔定理
- 拉格朗日中值定理
- 柯西中值定理
不过本文档的宗旨是快速提供微积分入门知识,这不是专业数学课,很多细节不过多探讨,这里我们只谈论「拉格朗日中值定理」,实际上「罗尔定理」是「拉格朗日中值定理」的特殊情形。
拉格朗日中值定理
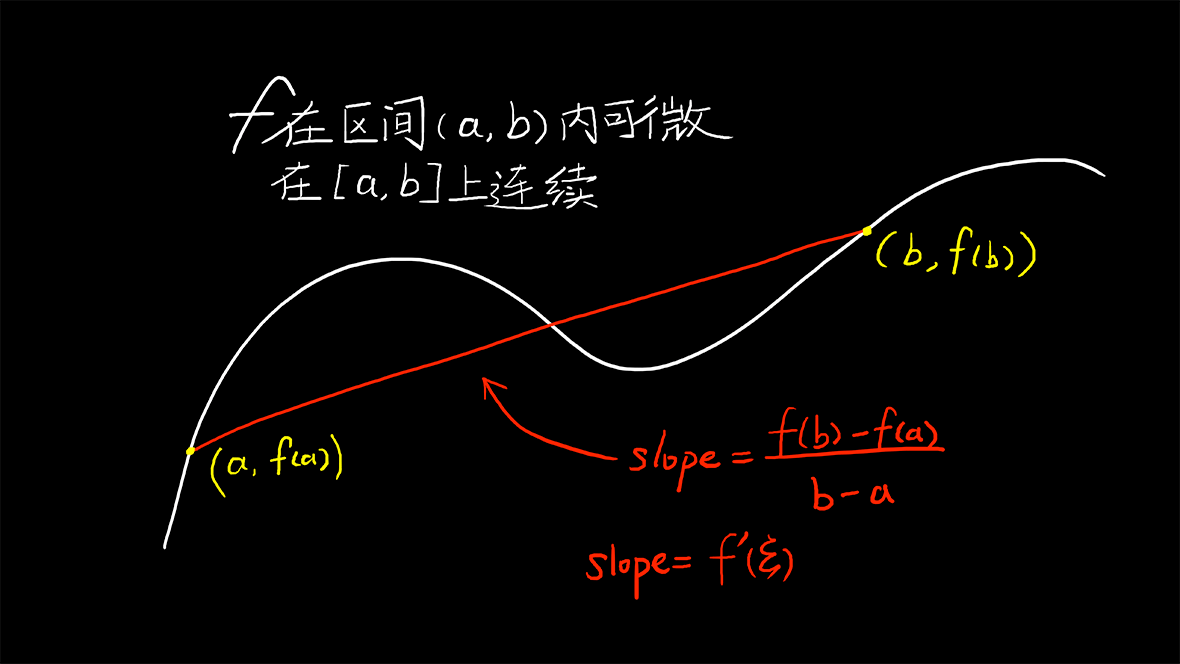
图中红色直线的斜率可以用f^\prime(\xi)来表示。
\displaystyle f^\prime(\xi)=\frac{f(b)-f(a)}{b-a}\\{}\\ \Rightarrow f(b)-f(a)=f^\prime(\xi)(b-a)\\{}\\ f(b)=f(a)+f^\prime(\xi)(b-a)\\{}\\ a < b
推论:
当f^\prime>0,f递增;当f^\prime< 0,f递减;当f^\prime=0,f是个常数。
\displaystyle f^\prime(\xi)>0\Longrightarrow f(b)>f(a)\\{}\\ f^\prime(\xi)<0\Longrightarrow f(b)< f(a)\\{}\\ f^\prime(\xi)=0\Longrightarrow f(b)=f(a)\\{}\\ \min f^\prime\leq\frac{f(b)-f(a)}{b-a}=f^\prime(\xi)\leq\max f^\prime\\{}\\ a< \xi< b,a\leq x\leq b
证明只需一张图即可: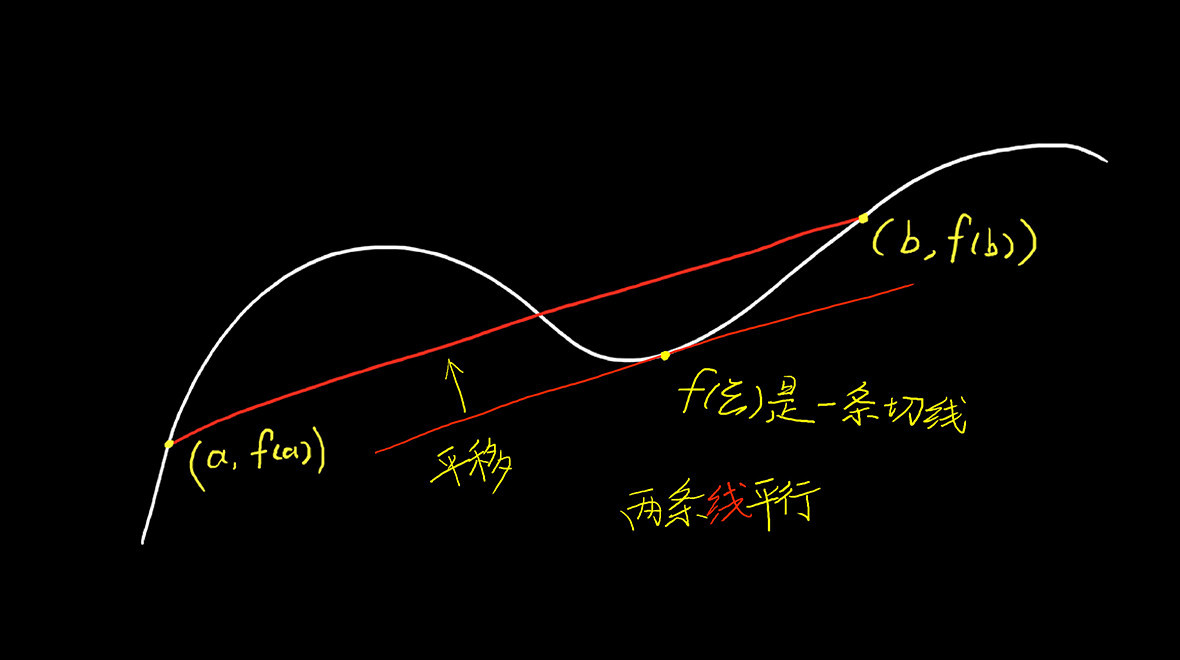

 单变量微积分
单变量微积分

 关于 LearnKu
关于 LearnKu



