微分方程与分离变量

微分方程#

微分方程不是我们这套文档的考虑范围，不过在此稍微讲点知识点，或许我之后会专门写微分方程的文档，微分方程分为「常微分方程」「偏微分方程」。
比如「谐振子基态方程」：

$\displaystyle \left(\frac{d}{dx}+x\right)y=0$

以上的$\displaystyle\left(\frac{d}{dx}+x\right)$ 是「量子力学」中的「湮没算符」，还有个「创生算符」是$\displaystyle\left(\frac{d}{dx}-x\right)$。

$\displaystyle \Rightarrow\frac{dy}{dx}=-xy\\{}\\ \Rightarrow\frac{dy}{y}=-xdx\\{}\\ \Rightarrow\int\frac{dy}{y}=-\int xdx\\{}\\ \Rightarrow\ln y=-\frac{x^2}{2}+c\\{}\\ \Rightarrow e^{\ln y}=e^{-\frac{x^2}{2}+c}\\{}\\ \Rightarrow y=ae^{-\frac{x^2}{2}},a=e^c\\{}\\{}\\ _{\color{red}general\color{none}solustion}y=ae^{-\frac{x^2}{2}},\forall a$

我们最后说了$\forall a$，是因为这是一个通解，通解不论$a$ 怎么取，它都是问题的解。

在实际应用问题中，构造出一个微分方程来描述情况十分重要，为了验证方程是否正确，需要解出它，然后看看是否和得到的一致。
是否可以解出$x$ 而不是$y$，隐式方程中，常常卡在$x$ 关于$y$，$y$ 关于$x$ 的转换上，具体指定一个函数有时很复杂，把$y$ 看作关于$$的函数不一定是最好的办法。
通过导数和二阶导数的信息得到函数本身的信息，常微分方程就以这个为基础。

分离变量#

$\displaystyle \frac{dy}{dx}=f(x)\\{}\\ dy=f(x)dx\\{}\\ y=\int dy=\int f(x)dx$

把原来的求导式转换成积分式，用$y$ 的导数$f(x)$ 的积分去解出$y$。注意，我们之前看到太多$\displaystyle\frac{dy}{dx}=f^\prime(x)$，那是因为我们在表达$y=f(x)$，现在我们看到$\displaystyle\frac{dy}{dx}=f(x)$ 实际上是表达$y^\prime=f(x)$，所以不要搞错了。

以上分离变量法解析：

$\displaystyle \frac{dy}{dx}=\underbrace{f(x)}_{-x}\underbrace{g(y)}_{y}\\{}\\ \frac{dy}{g(y)}=f(x)dx\\{}\\ \underbrace{H(y)=\int\frac{dy}{g{y}}}_{\ln y}\\{}\\ \underbrace{F(x)=\int f(x)dx}_{-\frac{x^2}{2}}\\{}\\ H(y)=F(x)+c$

$H(y)=F(x)+c$ 这种方程是个隐式方程，写成显示为：

$\displaystyle y=H^{-1}(F(x)+c)$

实际问题中，求微积分部分会很好算，最后求逆却很麻烦，所以有时候只要求出隐式形式就可以了，当然能够写出显式形式还是好的。

构造微分方程#

我们来试着构造个微分方程吧。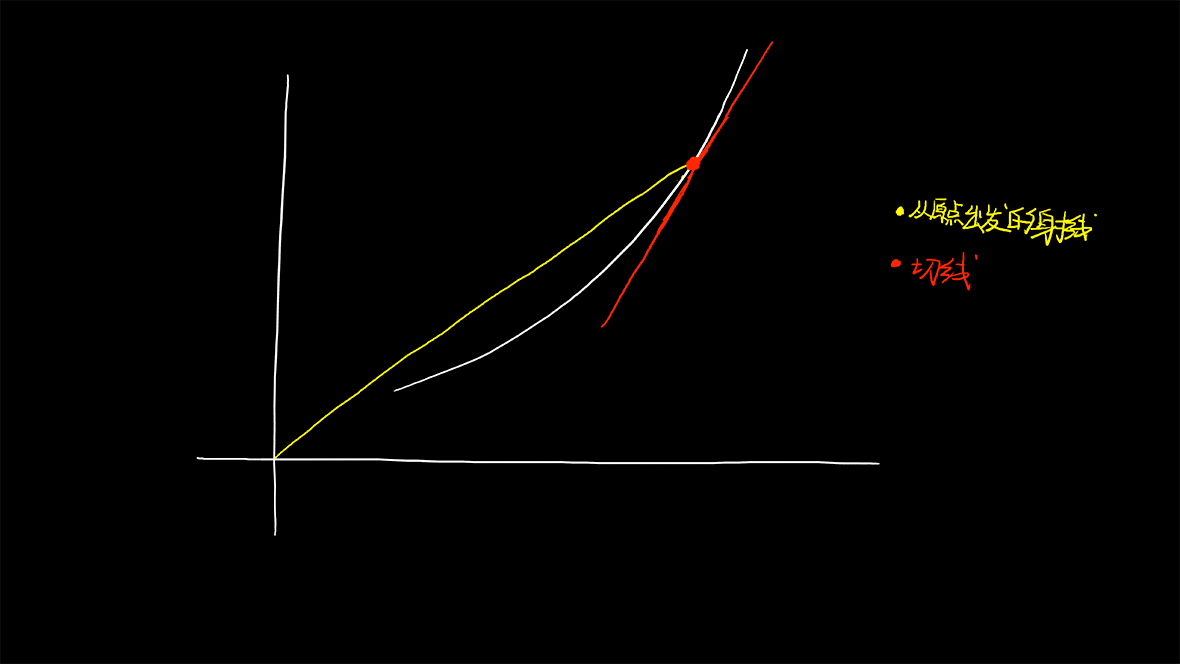

这个红色切线的斜率是黄色射线斜率的两倍，我们来构造微分方程：

$\displaystyle \frac{dy}{dx}=2\frac{y}{x}$

以上就是常微分方程的简单介绍，真正的微分方程的知识会在微分方程的文档里面。