反函数求导
反函数
用隐函数微分法可以求导任意反函数,只要知道原函数的导数。
反函数定义:
g=f^{-1},f=g^{-1}
反函数求导
例:
y=\tan^{-1}x
\tan^{-1}x=\arctan x
两边同时取正切:
\displaystyle \tan y=x\\{}\\ \frac{\mathrm{d}}{\mathrm{d}y}\tan y=\frac{\mathrm{d}}{\mathrm{d}y}\frac{\sin y}{\cos y}=\frac{1}{\cos^2y}=\sec^2y\\{}\\ \frac{\mathrm{d}}{\mathrm{d}x}(\tan y=x)\\{}\\ \frac{\mathrm{d}}{\mathrm{d}y}\tan y\frac{\mathrm{d}y}{\mathrm{d}x}=1\Rightarrow\frac{1}{\cos^2y}y^\prime=1\\{}\\ \therefore y^\prime=\cos^2y
我们需要把y^\prime的结果写成关于x的表达式:
\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}\tan^{-1}x=\cos^2(\tan^{-1}x)
这个结果形式看起来有点复杂,但结果是没问题的,实际上可以让它换一种形式:
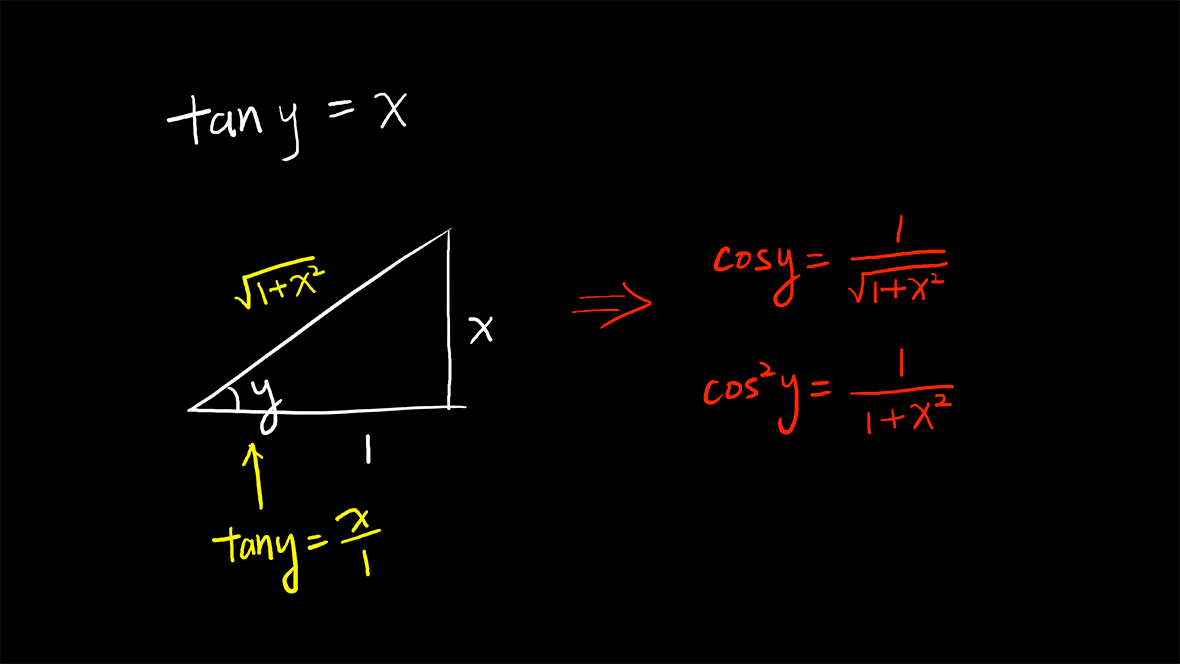
我们把y与x的关系通过直角三角形的图展现出来,再从这个直角三角形中找到\cos y的表达式。最后我们可以把答案换一种写法:
\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}\tan^{-1}x=\frac{1}{1+x^2}

 单变量微积分
单变量微积分

 关于 LearnKu
关于 LearnKu



