导数
函数定义
我们来看基本的函数:
y=f(x)
这里,y是函数f的「因变量」,x是函数f的「自变量」。
y用于存储一个对应于相应的x经过f()处理过后的值。
也可以理解为x是输入值,f是函数,y是输出值。
有时候在处理函数与函数的关系的时候,我们的关注焦点在函数上,而不在输入值和输出值上,所以那种情况下把f(x)缩写成f。
导数定义
导数,也叫「导函数值」,又名「微商」,是微积分中的重要基础概念。
我们来看下面的函数图: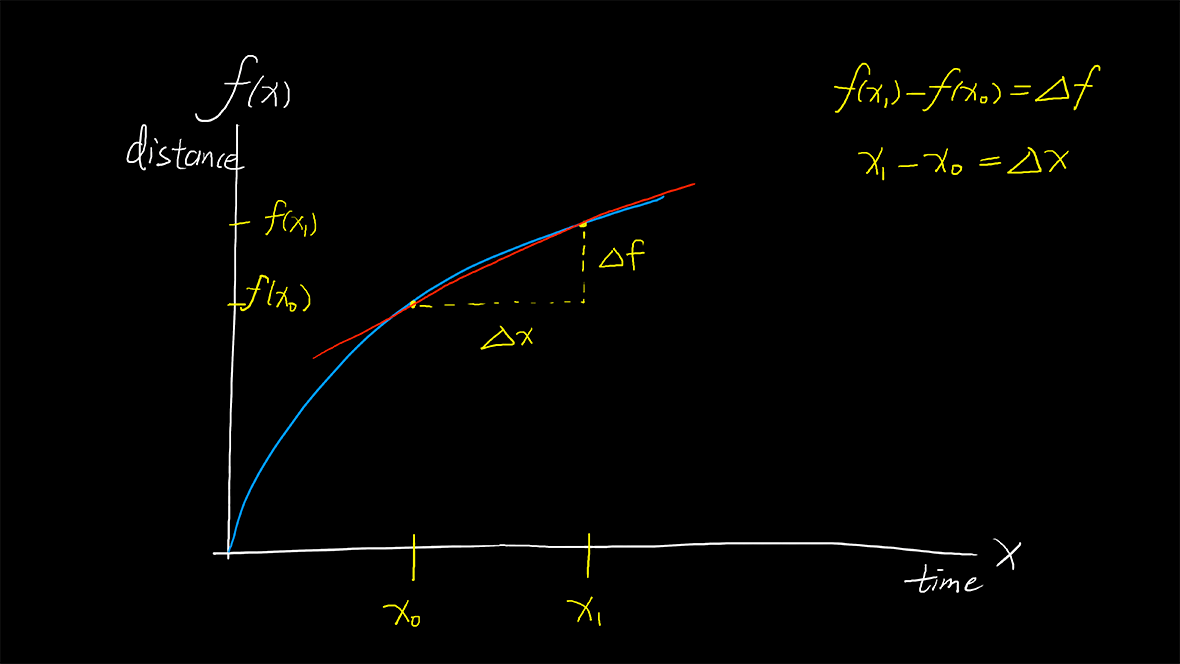
可以看到这个平面直角坐标系的纵轴f代表距离,横轴x代表时间,蓝线为函数f(x)。
我们随便在函数f(x)中取了两个点x_0,x_1。
得到对应的f(x_0),f(x_1)。
最终我们有了两段长度量\Delta x,\Delta f,分别是经过的时间量和经过的距离量。
现在我们用「距离量」除以「时间量」得到的当然是「速度值」。
\displaystyle \frac{\Delta f}{\Delta x}=avgrate
不过我们得到的只是这段时间中的平均速度,一系列平均速度组成的是一条直线函数。
这个速度值刚好对应的是图中的红色直线这个函数,直线函数的形式:g(x)=ax+b。b代表偏离量,a代表「斜率」。
而我们的\frac{\Delta f}{\Delta x}刚好就是个斜率值,相当于红色直线的a。也就可以说这条红色直线函数为:
\displaystyle g(x)=\frac{\Delta f}{\Delta x}x+b
红色直线的a实际上就是这个平均速度,这个平均速度值代表的就是红色直线的斜率:
g(x)=avgrate\cdot x+b
上面b是个常数,实际上在微积分函数表达式中一般记作c(constant 常数),我们在积分的章节中会明白这个c是怎么冒出来的(或许你在微分章节就看出来了)。不过在机器学习的线性回归模型中,这就记作b。
我们观察红色直线,会发现随着时间的增长,相应的距离也在增长,但不会发现有减速的迹象,而我们观察函数f(x),实际上会随着时间的增长而减速。这里的红色直线只不过是函数f(x)中的一条割线。我们的\frac{\Delta f}{\Delta x}是这条割线的斜率。
假设蓝线f(x)是关于某人开车去某个目的地的时间距离函数。
当我们问:求x_0到x_1的时间段里的平均速度是多少?
我们能很快给出答案,但是当我们问:求时间在x_0时,速度是多少?我们就无法简单用\frac{\Delta f}{\Delta x}来给出答案了。
现在我们看下图:
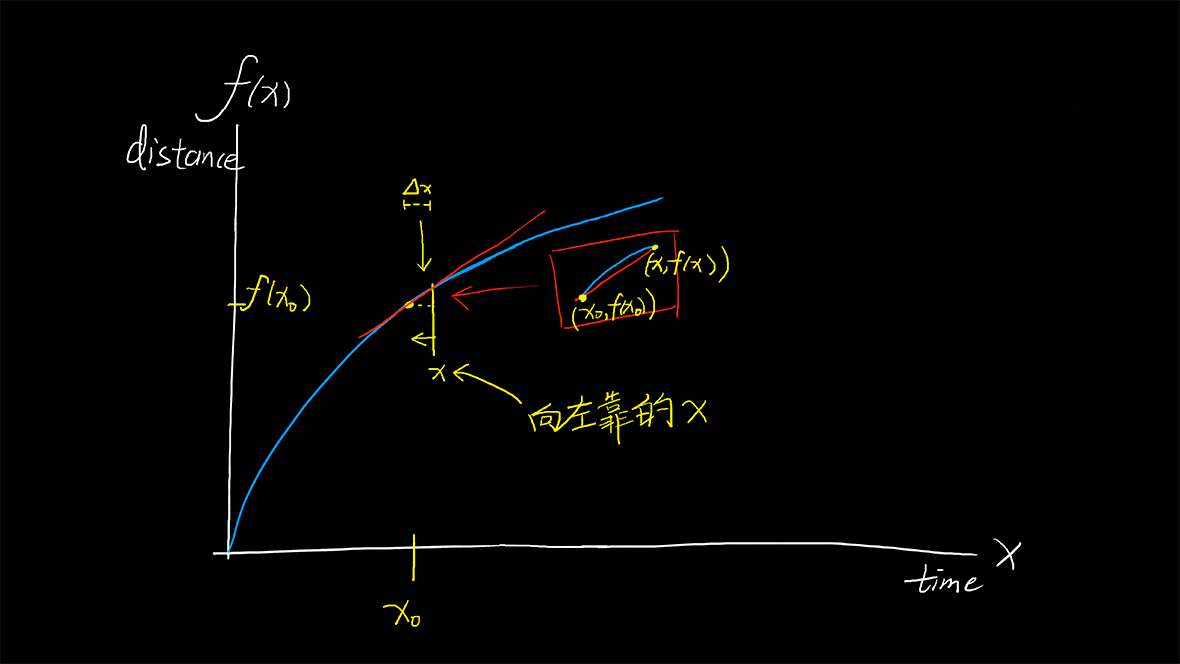
这时候我们的x_0没有动,而我们的x_1不见了,我们任意取一点在x_0的右边,记作移动的x,图中的红色直线依然还是f(x)的割线,虽然\Delta x很短但不是0,可以看到图中的x和x_0离得很近,我们可以看到x在向左靠,我们想让x和x_0重叠,这时候红色直线将不会再是蓝线f(x)的割线了,而是切线,而这个切线将不会再是「平均速度」,而是「瞬时速度」。
如下图:
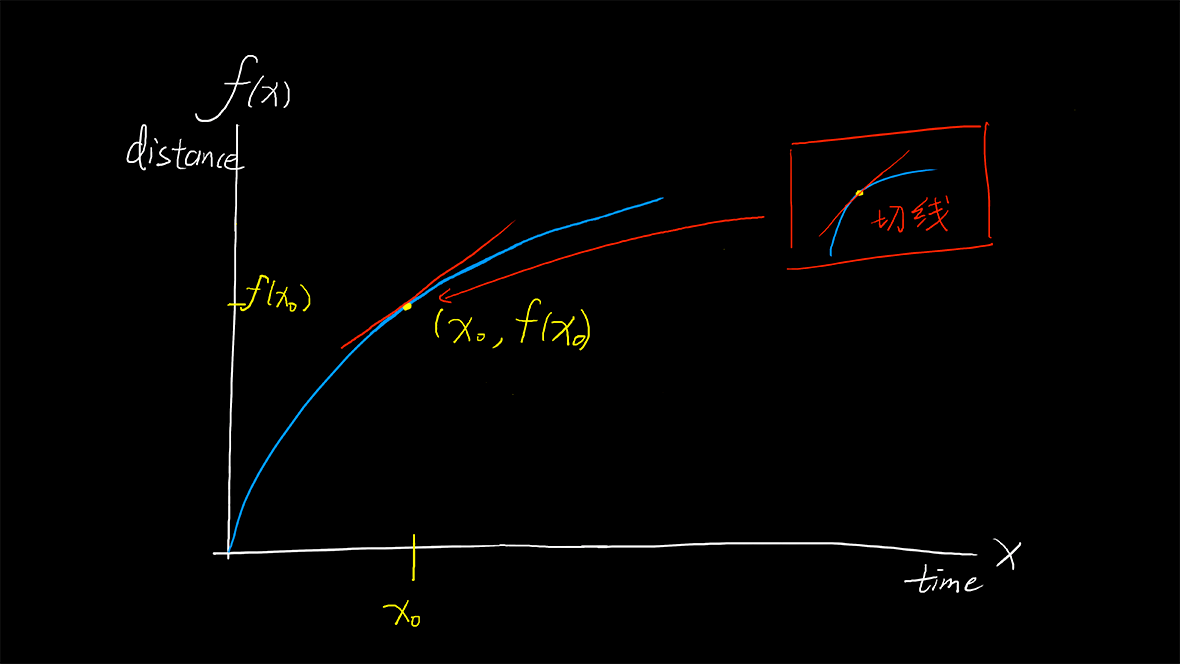
我们现在让移动的x点固定在了x_0的位置,使他们重叠了,那这个时候\Delta x岂不是0了?没错,他不能简单说等于0,而应该说\lim\limits_{\Delta x\rightarrow0}。
现在我们想知道这个红色直线的斜率「点切线斜率」:
\displaystyle \lim\limits_{\Delta x\to0}\frac{f(x_0+\Delta x)-f(x_0)}{x-x_0}
上述公式是差商公式,这公式是一切的开始。
当\Delta x\to0时,\frac{\Delta f}{\Delta x}应该记作\frac{\mathrm{d}f}{\mathrm{d}x}。
所以:
\displaystyle \frac{\mathrm{d}f}{\mathrm{d}x_0}=\lim\limits_{x\to x_0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}
这里的x_0是个固定值,当我们要求出f(x_0)这点的瞬间速度值,相当于求出\frac{\mathrm{d}f}{\mathrm{d}x_0}。
不过我们想直接知道一个函数f(x)的导函数,方便我们直接找出f(x)任意的x点对应的斜率。
这个导函数记作f^\prime(x),这是一个导函数的完整表达,因为带上了此函数的自变量,实际上在探讨函数与函数之间的关系的时候我们会使用不带上此函数的自变量的表达方式:f^\prime。
由于微积分中有莱布尼茨符号和牛顿符号,符号长得不一样,但意思都一样,为了避免符号混淆,可以了解以下等式:
\displaystyle f^\prime(x)=\frac{\mathrm{d}f}{\mathrm{d}x}
导函数定义:
如果函数y=f(x)在开区间内每一点都可导,就称函数f(x)在区间内可导。这时函数y=f(x)对于区间内的每一个确定的x值,都对应着一个确定的导数值,这就构成一个新的函数,称这个函数为原来函数y=f(x)的「导函数」记作y^\prime、f^\prime(x)、\frac{\mathrm{d}y}{\mathrm{d}x}或\frac{\mathrm{d}f(x)}{\mathrm{d}x},简称导数。
理解导数可以从「平均变化率」到「瞬时变化率」来理解:
\displaystyle \frac{\Delta y}{\Delta x}\rightarrow\frac{\mathrm{d}y}{\mathrm{d}x}

 单变量微积分
单变量微积分

 关于 LearnKu
关于 LearnKu



